血糖分析仪线性回归方法

廖弘毅

(北京市海淀区计量检测所，北京 100083)



血糖分析仪线性回归方法

廖弘毅

(北京市海淀区计量检测所，北京 100083)

在计量检测工作中，经常面对大量的数据处理，而对数据进行线性回归是数理统计中最常用的方法之一。本文以便携式血糖分析仪线性误差计算为例，用线性回归的三种方法对数据进行分析处理，并进行了相互验证。

血糖分析仪；线性回归；数据处理；线性误差

0 引言

JJF 1383—2012《便携式血糖分析仪校准规范》于2013年3月21日正式实施，按照规范中的规定，便携式血糖分析仪的线性误差不超过±5.0%。规范中明确了线性误差的校准方法和计算公式，并指明线性回归的方法求出曲线的截距a和斜率b，但是如何通过线性拟合计算出回归曲线a和b，规范并没有明确说明。本文较详细地探究了线性回归的计算过程，为一线工作者快速掌握便携式血糖分析仪线性回归计算，准确执行JJF 1383—2012校准规范提供了较为便捷的方法。

1 实验数据

依据JJF 1383—2012《便携式血糖分析仪校准规范》要求，列举一组血糖分析仪线性校准数据，详细分析线性回归的几种方法。

按照规范要求检测的数据如表1所示。

表1 血糖分析仪线性误差校准数据 单位：mmol/L

2 线性回归的方法

2.1 原理推导计算法

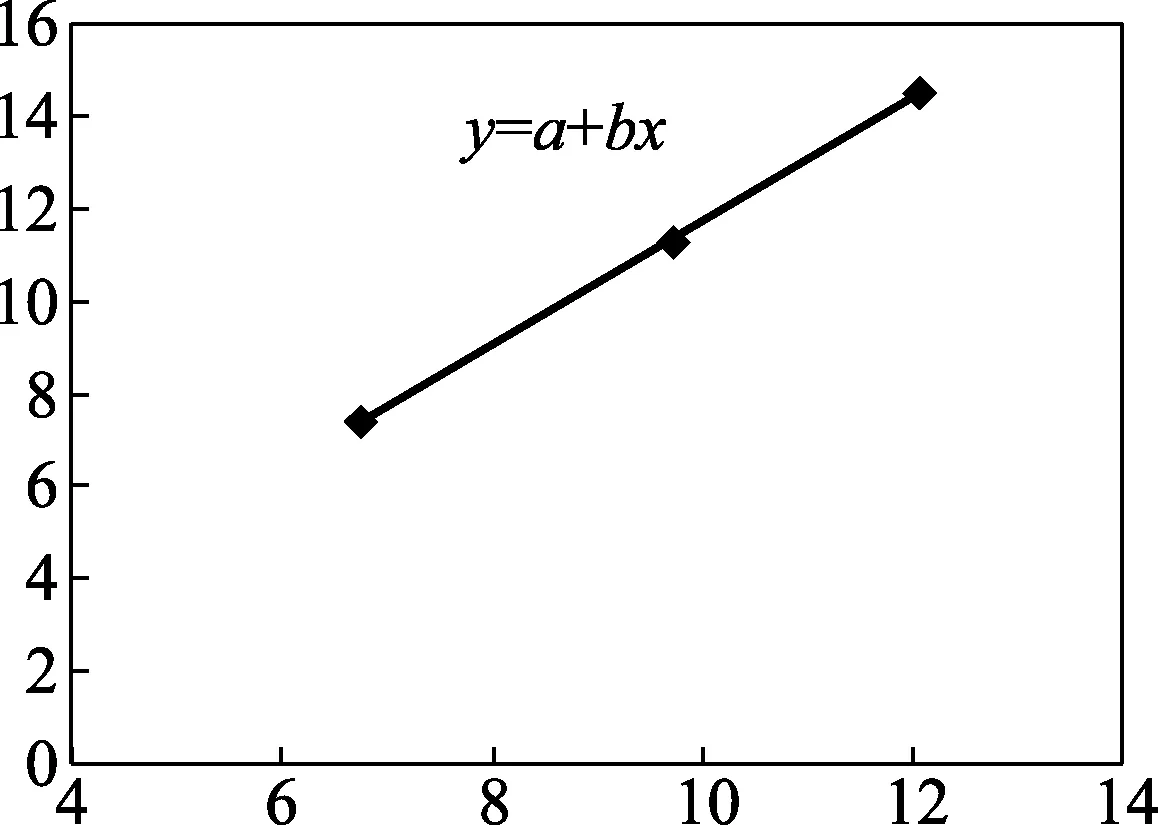
图1 血糖分析仪线性拟合曲线

曲线拟合最基本的原理是基于最小二乘法的应用，如何将上述曲线(图1)拟合出线性回归方程y=a+bx

式中，x为自变量，此处为血糖标准物质标称值；y为因变量，此处为测量结果平均值。

我们根据最小二乘法原理,回归分析式推导出：

(1)

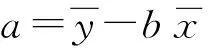
(2)

分别计算出上述推导公式中的各分量如表2所示。

计算可得：b=1.3339

a=-1.6185

回归方程：y=1.3339x-1.6185

这样利用上述公式完成拟合，从原始数据推导出斜率与截距，运算过程涉及8个分量，由此可见运算过程相当繁琐。因此需要从实际应用出发，寻求更加简便的方法，完成线性拟合，得出回归方程。

表2 回归分析分量计算表

2.2 计算器在线性回归中的应用

使用具有回归功能函数的计算器对测量数据进行回归处理,既准确快速,又可省去作图,适宜现场检测中及时验证。计算器操作程序如表3所示。

具有线性回归功能的科学计算器较多,常见的科学计算器厂家有SHARP和CASIO。现就上述血糖分析仪检测数据(参见表1)，利用CASIO(fx-3600P)计算器进行线性回归运算，从而得出线性回归方程y=a+bx中的截距a,斜率b。

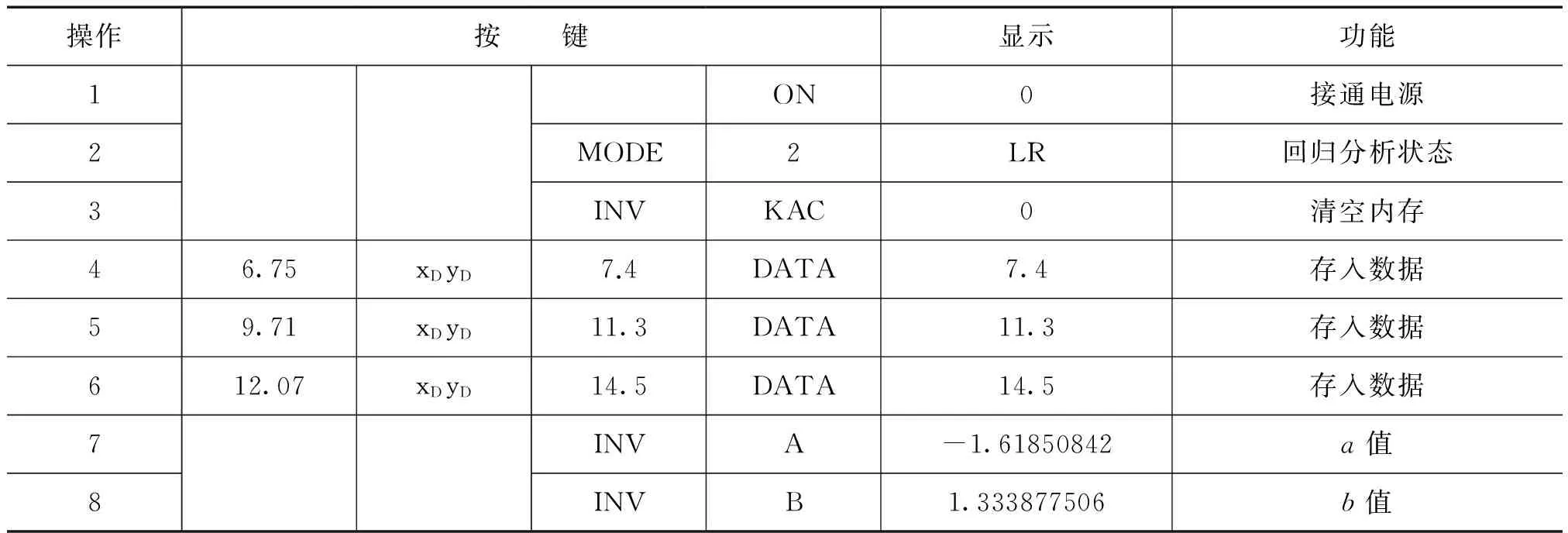
表3 计算器操作程序

用计算器直接得出：y=1.3339x-1.6185。这个结果与原理推导计算法运算的结果是一致的。

2.3 利用EXCEL在线性回归中的应用

根据血糖分析仪的测量数据(参见表1)，将血糖标准物质标称值设为x值,测量结果的平均值设为y值。利用Microsoft Excel进行绘图，运算步骤为：

1)打开Microsoft Excel软件，生成一个空白表Book1；

2)将测量数据输入表格；

3)在“菜单”中，依次选择“插入”、“图表”、“标准类型”、“xy散点图”；

4)选中“数据区域”，并在“系列”中确认x、y值；

5)在“标题”中“图表标题”，输入“线性回归”，“完成”插入图表；

6)在“菜单”中，依次选择“图表”、“添加趋势线”、“类型”、“线性”/“选项”、“显示公式”、“确定”;

7)完成线性回归图表的绘制，如图2所示。

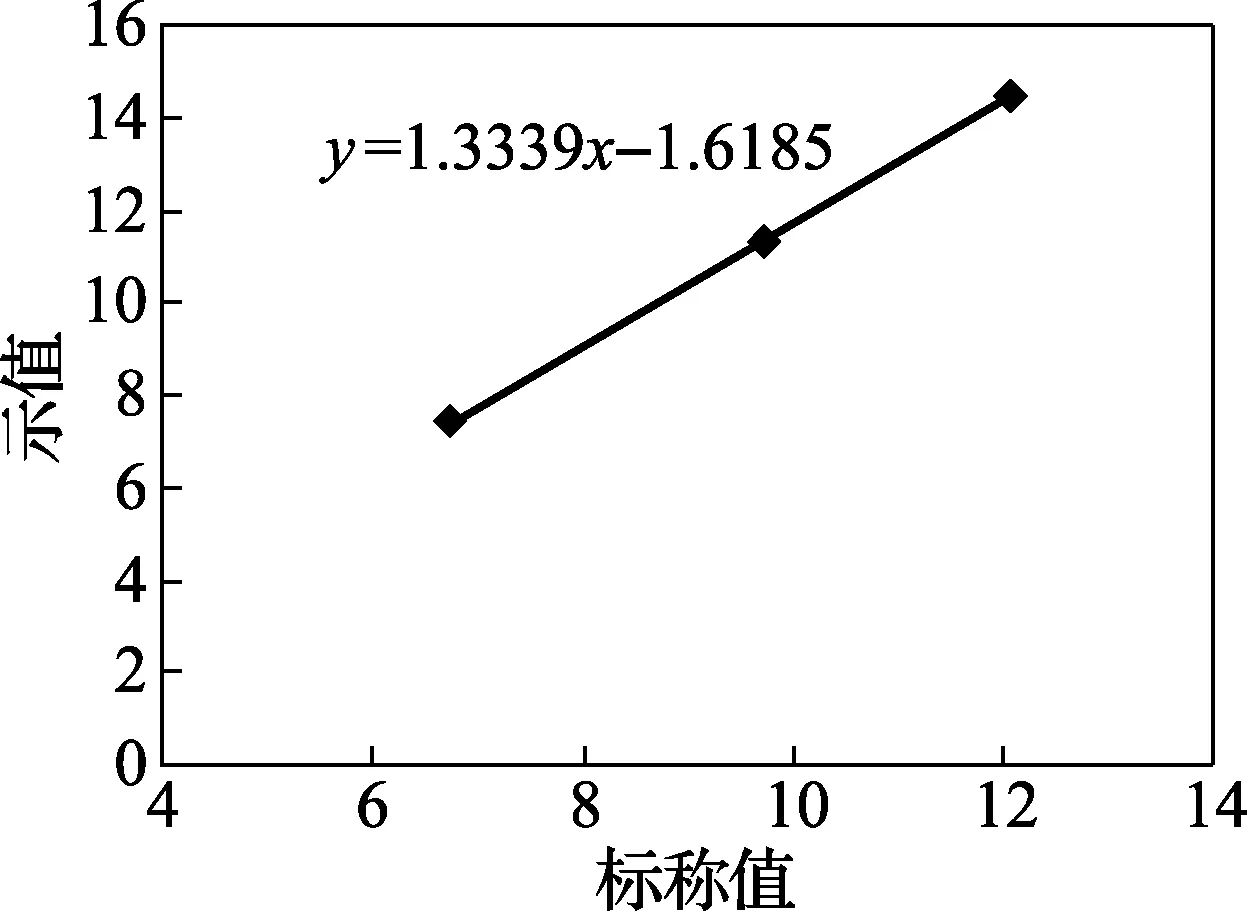
图2 Excel生成的线性拟合曲线

由图2中可以清晰读出回归方程：y=1.3339x-1.6185，并得出截距a和斜率b。

Excel软件提供了更加简便的方法进行数据的线性回归，利用插入常用函数直接可得回归方程的a和b。

通过表1的数据引出以下两个函数：

1)求线性回归拟合线方程的截距：

INTERCEPT(known_y’s,known_x’s)

2)返回经过给定数据点的线性回归拟合线方程的斜率：

SLOPE(known_y’s,known_x’s)

分别在Microsoft Excel中，输入函数所需的x和y的数据组(表1)。

a=INTERCEPT(Y1:Y3,X1:X3)=-1.6185，b=SLOPE(Y1:Y3,X1:X3)=1.3339，从而回归方程：y=1.3339x-1.6185。

3 线性回归讨论

JJF 1383—2012校准规范在计算线性误差时只要求低、中、高值3个数据点进行线性回归计算。但按线性回归要求，通常应有5个点进行回归才有意义。为了验证这个问题，将实验检测点增加至5个进行回归。校准数据见表4。

表4 扩展后的血糖分析仪校准数据 单位：mmol/L

根据1.3所述的方法，利用Excel重新进行线性回归计算，结果如图3所示。

a=INTERCEPT(Y1:Y3,X1:X3)=-1.5922，b=SLOPE(Y1:Y3,X1:X3)=1.3152，因此回归方程：y=1.3152x-1.5922。

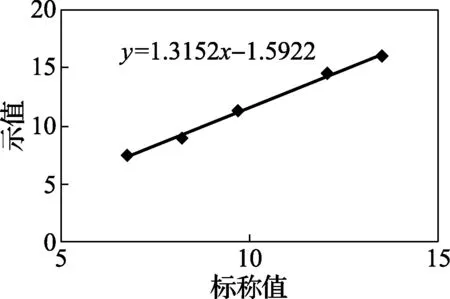
图3 5点校准数据线性拟合曲线

根据5点的回归结果，与校准规范要求的3点校准回归曲线一致率大于98%，证明上述三种回归方法的计算结果是可信的。

4 结束语

以血糖分析仪校准过程中的线性回归计算为例，介绍了三种进行线性回归的方法，并对三种方法的优缺点进行了讨论。线性回归还有一些其他的方法，本文只是抛砖引玉进行一些运算方法的分析。线性回归广泛运用于化学分析领域和不确定度分析，希望本文能给读者以启示，有助于基层工作者快速掌握简便的线性拟合计算方法。

[1] JJF 1383—2012便携式血糖分析仪校准规范[S].北京：中国质检出版社，2013

[2] 潘忠泉,等.酶标分析仪吸光度标准物质的研制[J].计量技术,2005(4):39-41

[3] 梁晋文，陈林才，何贡.误差理论与数据处理[M].北京：中国计量出版社,2008

[4] 董凤鸣，周萍.EXCEL在一元线性回归分析中的应用[J].科技信息,2007(12):144-146

[5] 王月明,庄金智.线性回归分析及其在工作曲线法中的应用[J].云南教育学院学报,1995(4):50-54

10.3969/j.issn.1000-0771.2015.11.21