三针测量外螺纹单一中径测力压陷修正的讨论
2015-06-09刘远模
刘远模
(成都艾立特螺纹工具有限公司,成都 610081)
三针测量外螺纹单一中径测力压陷修正的讨论
刘远模
(成都艾立特螺纹工具有限公司,成都 610081)
本文讨论三针测量螺纹单一中径的测力压陷修正的计算,国家标准GB/T 28703—2012与校准规范JJF 1345—2012给出的计算不同,有必要对这个题目进行讨论,以便为它们的正确贯彻提供参考。本文证明了JJF 1345—2012中7.2.1.3“探针变形的修正”不适用于三针测量,而GB/T 28703—2012则适用。
三针;螺纹单一中径;测力压陷修正;接触变形
0 引言
国家标准GB/T 28703—2012《圆柱螺纹检测方法》与校准规范JJF 1345—2012《圆柱螺纹量规校准规范》对三针测量螺纹单一中径的测力压陷修正的计算给出不同公式,计算和实验证明其结果有显著差异,本文不仅给出这些公式,并用3个规格的实验数据,获得了多种计算方法的计算结果,得出JJF 1345—2012不适用于三针测量及其他相关结论。
1 三针测量的单一中径公式
由文献[2,5]可得用三针跨线测量外螺纹单一中径d2的计算公式为
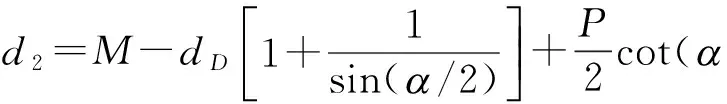
(1)
式中,M为跨线测量值;dD为量针直径;P为螺距标称值;a /2为牙侧角即牙型角的一半;A1为螺旋升角修正量;A2为测力压陷修正量。
关于A1(即斜置误差的反号)的讨论见文献[3],本文讨论A2。
2 JJF 1345—2012中的相关讨论(本文简称为JJF)
规定只能用于圆柱对称螺纹量规。
接触变形是测力使两物体的理论接触点或线变化,从而两物体沿作用力的方向相互接近的量。这种变形通常限制在材料的弹性极限内。理论上,球与平面的接触为点,量针圆柱与螺旋面的牙侧的接触也为点,在测量力的作用下,前者的作用边界为圆,后者的作用边界为椭圆。
在文献[2]中,7.2.1.3“探针变形的修正”测力压陷修正量A2按其中的式(6b)计算。这种计算是以球与平面的接触变形为基础,再用量球与V形槽接触的受力和变形关系,获得量球在一侧牙槽直径上的变化量,最后求得测力导致的直径上的修正量A2。
即该文献中式(6)、(6a)和(6b)分别为本文的式(2)、(2a)和(2b)。
(2)
式中,ω0为球和平面接触的变形;vi为泊松系数(钢为0.28,红宝石为0.25),i=1,2;F为测量力(垂直于平面),单位N;Ei为弹性模数(钢为2×105N/mm2,红宝石为4×105N/mm2),i=1,2;dD为探针直径。
ωv0=(sin(a /2))-5/3(1/2)2/3ω0
(2a)
式中,ωv0为V形槽中球的变形。
A2=2ωv0
(2b)
由该节叙述可知:
1)变形修正的依据是按式(2)计算的球与平面的接触变形,而不是量针圆柱与空间曲面螺旋面牙侧的接触变形。显然该式计算值与三针直径相关,而与被测件大小无关。
2)实际垂直于牙侧的测力是用量球与V形槽接触的受力关系及其变形对直径方向的影响也是基于V形槽关系而不是有螺旋升角的牙侧曲面。单侧接触变形用式(2a)计算。
3)螺纹直径上的测量力修正量A2按式(2b)计算。对于三针测量,A2按式(2b)计算是错误的,因为螺纹直径上单侧是一根量针而另一侧是两根量针。
4)摩擦力的影响只泛泛谈到,而没有引入计算方法。对三针测量没有给出计算变形公式,于是只好用上述公式代替。
因此按该校准规范计算三针测量外螺纹单一中径的测力修正量A2可能产生较大误差是不足为奇的。尽管上述内容与EA—10/10即文献[5]一致。
3 GB/T 28703—2012中的相关讨论(本文简称为GB)
在文献[1]中,6.1.1.3“三针法”的δF和dm就分别是上述A2和dD,于是该文的式(17)~(24)分别为本文的式(3)~(10)。
A2=1.63f
(3)
式中,f为单根量针与螺纹两牙侧接触的受力压陷量。
(4)
式中,δ为量针与牙侧面的接触变形;g 为测力方向与牙侧面切点处压力方向的夹角。
(5)
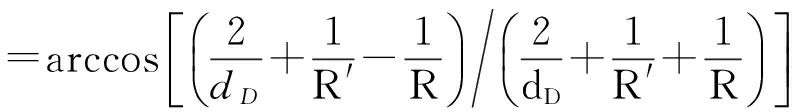
(6)
(7)
(8)
(9)
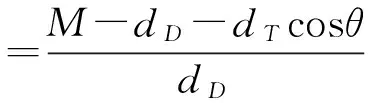
(10)
式中,F为测力;dT为牙侧面切点处的直径;R和R′分别为牙侧面切点处的主曲率半径;n为螺纹线数;P为螺距。
式(5)、(6)、(8)和(9)与文献[6]中相应公式类似,但作了必要的改进。式(8)是V形槽中牙侧面切点处的最大曲率半径。式(7)考虑了摩擦力对测量的影响。
4 其它相关资料讨论
1)在文献[4]中详细推导了三针测量螺纹单一中径的测力压陷计算公式,该公式组相当复杂但用程序就能很方便的求得结果(程序中K2就是A2),本文取名为“准确”。
2)由欧洲保加利亚QUALISYST有限公司编制的程序QMSTHRPD(简称QMSys)是用量针或量球检验螺纹中径的计算软件。将已知值输入可得检验计算结果;将测量值输入可得测试计算的中径值。包含A1的中径计算值用文献[5]中的Brendt公式计算,A2用Lechowski方法计算。
文献[1]即GB/T 28703—2012中式(5)的系数1.695就顾及到与QMSys软件实验结果一致的效果。
3)德国L&WGmbH公司的QMSOFT软件用途较广,对螺纹量规可以给出螺纹量规使用尺寸,并且可以进行检验计算和测试计算。本文简称为QM32。
4)在JJF中已被代替的JJG 888—1995,简称JJG,仅供参考。
5 螺纹单一中径的三针测量程序
图1用程序“螺纹单一中径的三针测量”中校准规范计算方法计算文献[2]的7.2.1.3“探针变形的修正”的计算示例,计算结果A2=-Δ2=0.0018mm,它是1.84μm取小数后4位的近似值。而用图1中程序的另外两种计算方法所得Δ2=-0.0007mm,显然在此校准规范的数值是此值的2.57(=1.8/0.7)倍。

图1 螺纹单一中径的三针测量
用上述程序计算文献[2]的表B.2中数据(即M=ΔL=65.2993,dD=3.4641,P=6.004,a =59.7°)得A2=-Δ2=0.0016,d2=60.1056,而该表列值分别为A2=0.0007和d2=60.1048,显然该表列出的两个数据不是用所述公式的计算值,但是该校准规范没有介绍表列数据来源。而用另外两个计算方法所得都分别为A2=K2=0.0005和d2=60.1046。
图1所示程序的三种计算方法中,“准确”根据文献[3-4]计算;“校准规范”根据文献[2]进行测试计算,其中的检验计算根据文献[7]计算;“国家标准”根据文献[1]进行测试计算,其中外螺纹中径根据文献[7]的苏宗康公式计算,内螺纹中径根据文献[1]对苏宗康的扩展公式计算,检验计算根据文献[7-8]公式计算。由文献[7]知,berndt公式有局限性,对锯齿螺纹可能产生显著误差,这是国家标准不采用它的原因,校准规范只适用于对称螺纹用它是不会出大问题的,但对于左右牙侧角因为偏差而不相等的螺纹,此时只能将两牙侧角之和得牙型角,其1/2得牙型半角。一般而言这样计算不会有问题。对校准规范因为其对测力压陷计算A2值得商榷,因此程序给出已作废的检定规程压陷计算供参考。
6 实验数据的计算和讨论
国家标准(GB)负责起草单位收集了多国资料并作了大量实验和比较分析研究,经工作组讨论和主管部门批准得到文献[1]。
取出典型的实验数据中几个规格进行讨论是有益的。
前述的几种程序计算方法对同一数据结果可能相同也可能有差异,如果差异不超过0.1μm可认为两种方法一致,如果差异不超过0.2μm可认为两种方法相当或等效。
一个中径的测量值M(或m)随测力F成反变,实际上是F与A2成正变,但理论上计算出的中径应不变化,那么这种计算方法是合理的。但由于存在测量误差和计算理论的不足够完善会导致计算中径有不太规则的对中径的偏移,于是用一组数值的均值代替是更能反映中径尺寸大小。
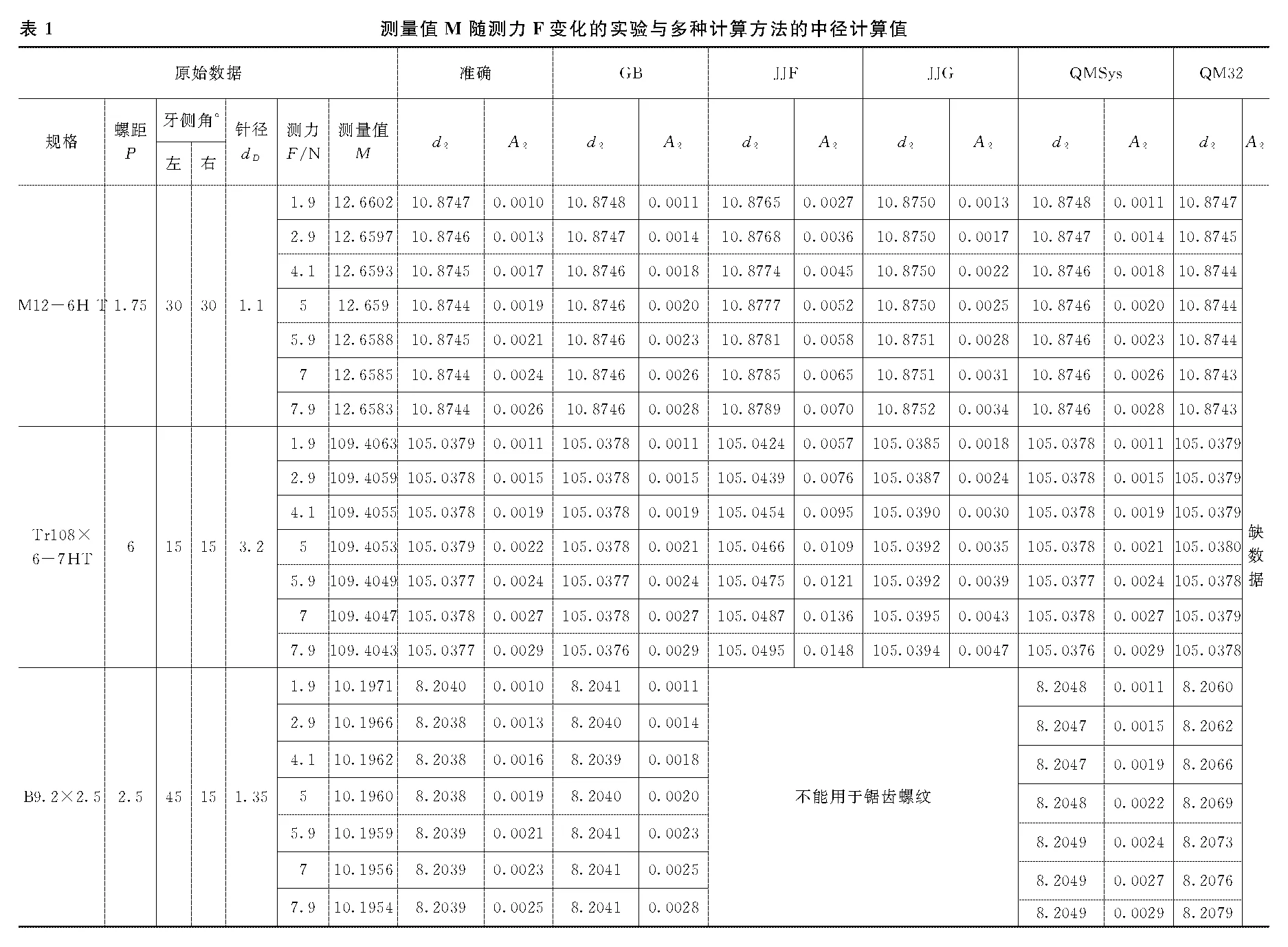
表1列出4个规格的测量值M随测力F变化的实验及多种计算方法的中径计算值。由此表可知:
1)对称螺纹,GB与QMSys中径结果一致;“准确”与QM32中径结果一致;GB与“准确”中径结果相当;JJF中径随测力的增大而增大,而前述4种中径基本不变。且JJF中径显著比前述4种中径大。因此JJF方法计算的中径有显著误差。图2是M12—6HT螺纹塞规的GB和JJF中径测试验证图示,GB中径数据基本不变,而JJF中径数据随测力的增大而增大,且后者的平均中径比前者大(10.8777-10.87464)=0.00306。两者相差显著。
2)锯齿螺纹,GB与“准确”中径结果相当;JJF只能用于对称螺纹,不能用于锯齿螺纹;QMSys和QM32因为用berndt公式不适用于锯齿螺纹,且QM32中径随测力的增大而增大而GB与“准确”及QMSys没有这种情况,它们中径基本不变。图3是锯齿螺纹B9.2×2.5外螺纹的“准确”和QM32中径测试验证图示,“准确”中径数据基本不变,而QM32中径数据随测力的增大而增大,且后者的平均中径比前者大(8.20693-8.20387)=0.00306。两者相差显著。
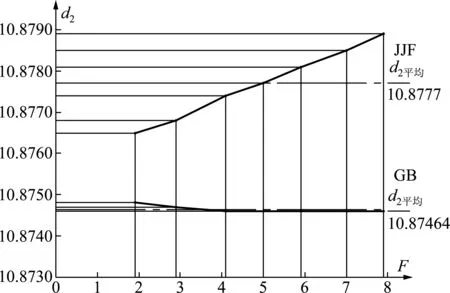
图2 M12—6HT螺纹塞规的GB和JJF中径测试验证
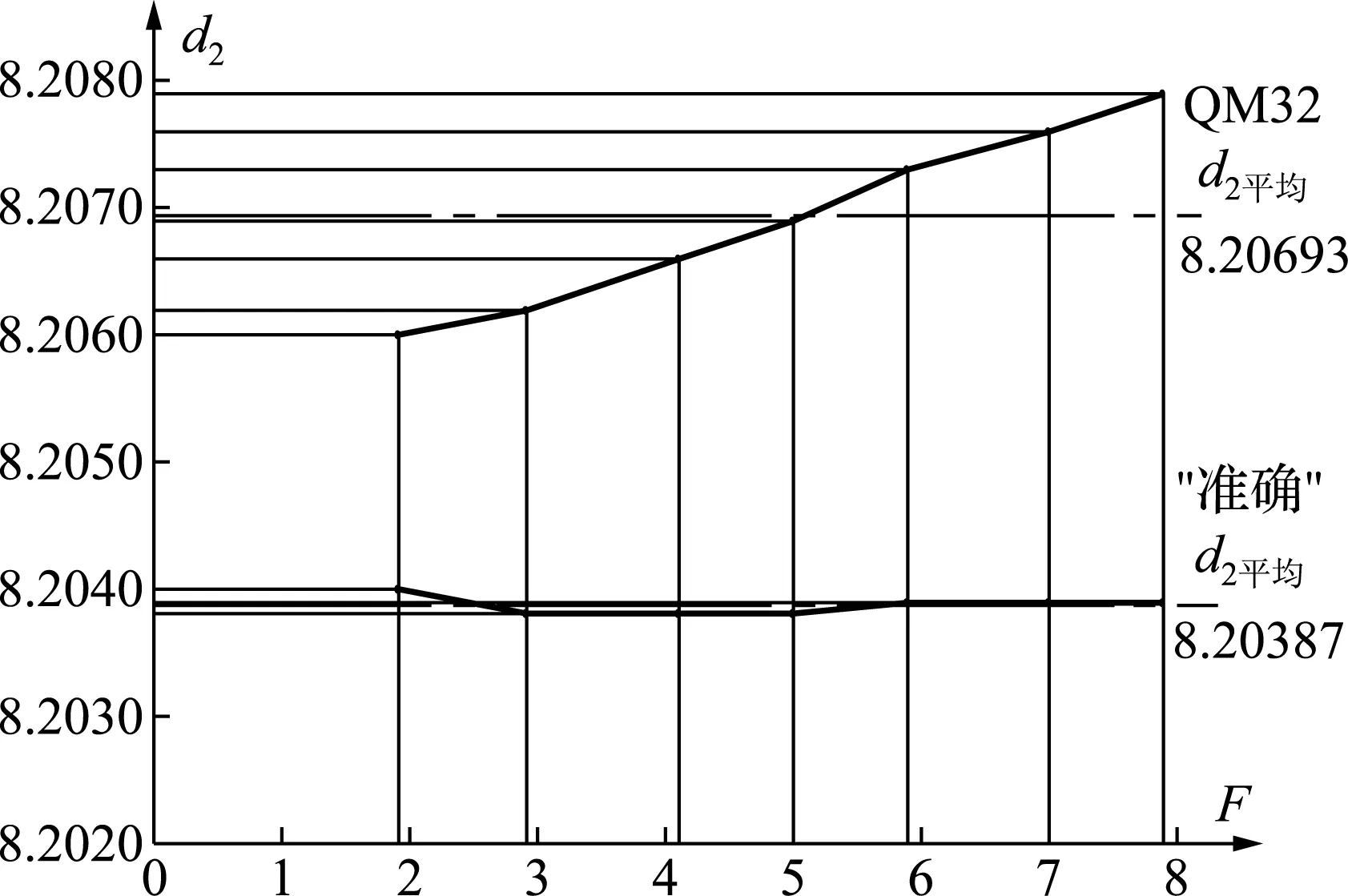
图3 B9.2×2.5(45°,15°)外螺纹的“准确”和QM32中径测试验证
7 结束语
由公式(1)可知,三针测量的测力压陷修正A2,是确定单一中径数据的一项重要因素,因此他是不可忽略的计算。这也是评估单一中径测量不确定度的一项重要因子。
对于对称螺纹,用国家标准、“准确”、QMSys和QM32计算的A2值是等效的;校准规范计算数值显著偏大,推荐不用,何况该规范的表B.2都不用这种计算,欧盟中的实用软件(QMSys和QM32)也没有采用这种计算。
对于锯齿螺纹,用国家标准、“准确”计算的A2值是等效的,推荐不用QMSys或QM32计算值,因为它们不仅存在berndt公式的系统误差,可参考文献[7],且QM32可能存在理论误差,因为其计算值随测力的增大而增大,参看表1或图3。
[1] GB/T 28703—2012圆柱螺纹检测方法
[2] JJF 1345—2012圆柱螺纹量规校准规范
[3] 刘远模.螺纹单一中径的三针和量球法测量.计量技术,2014(1)
[4] 刘远模.三针测量螺纹的测力压陷计算公式的推导.机械工业标准化与质量,2011(4)
[5] EA Guidelines on the Determination of Pitch Diameter of Parallel Thread Gauges by Mechanical Probing EA-10/10:9~12
[6] 希纳德尔.三丝量法.机械工业出版社,1956:34~35
[7] 刘远模.螺纹单一中径的三针和量球法测量公式讨论.计量技术,2014(2)
[8] 刘远模.螺纹单一中径的三针和量球法测量公式再讨论.计量技术,2015(3)
10.3969/j.issn.1000-0771.2015.11.09
