基于PSO算法的公路养护决策优化研究

李 岩

（黑龙江工程学院经济管理学院，黑龙江哈尔滨 150050）

基于PSO算法的公路养护决策优化研究

李 岩

（黑龙江工程学院经济管理学院，黑龙江哈尔滨 150050）

针对公路养护决策中存在的问题，以路面养护为例，借助LDR指数建立养护决策模型，利用粒子群优化算法（PSO）决策模型，对不同路面条件下公路养护决策进行优化分析。研究成果将对公路养护提供决策支持，并提出利于公路养护资金优化的方法。

公路养护决策；优化决策；LDR指数；粒子群优化算法（PSO）

1 概述

公路是交通网络的主要组成部分，负担大量交通运输活动。车辆、气候、公路养护技术和方法等多方面因素对公路产生不同的影响。公路养护问题是目前交通领域重点研究的问题之一。同时，公路作为重要的资产，也应进行科学地养护管理以保持资产的价值。这表明公路养护决策工作既属于工程技术领域，也属于资产管理的范畴。经过长期的公路建设，中国各地方交通部门在长年投入大量公路建设资金后均有一定的资金压力。因此，在公路养护资源非常有限的情况下，如何科学预测和合理分配公路养护资金，就成为公路养护决策所面临的主要问题。

国内外学者对公路养护管理决策问题从不同角度进行研究，并取得了一定的研究成果。美国学者Gendreau和Soriano对路面管理系统（Pavement management system，PMS）进行分析，着重研究基于计算机系统的不同路面结构的成本效益分析方法和修复策略［1］。该系统已被美国加利福尼亚州等地的交通部门采用。新加坡采用遗传算法设计路面养护决策系统（Pavenet）［2］。美国学者S.Fallah-Fini等利用系统动力学理论，采用模拟仿真技术对高速公路养护动态决策进行研究［3］。国外对公路养护决策的研究工作更倾向于工程与管理实践，利用大量数据进行系统分析研究。我国对公路养护系统的研究工作主要在20世纪80年代展开。邹培国建立了路面使用性能动态预测模型和自适应递推算法，并利用层次分析模型和启发式优化技术进行养护决策［4］。虞安军利用遗传算法对高速公路路面养护决策进行了优化研究，将NSGA-II应用于高速公路多目标路面养护决策优化问题［5］。刘军等针对公路养护资金有限的条件下，采用效果和费用比值作为效益指标，利用SCE算法对高速公路路面养护的整数规划求解［6］。我国学者对公路养护决策理论领域进行了深度研究，利用数学模型解决了多项决策问题。

2 公路破损评价

2.1 评价方法

国内外对公路破损评价方法有所不同，公路路面破损是其中的重点，因此，最具代表性的是对路面评价。从总体上讲，对于公路路面破损情况评价的作用之一即是为公路路面养护决策服务。因此，路面破损的评价结果会直接影响到路面养护决策的精度和效率。

我国在公路评价中采用了使用性能评价分项指标，即《公路技术状况评定标准》。公路技术状况评价（MQI）是以数量化指标为主的评价体系，其中包括路面、路基、桥隧构造物和沿线设施4个主要组成部分。其中，对路面（PQI）的评价指标主要包括：路面（PCI）、路面平整度（RQI）、路面车辙（RDI）、抗滑性能（SRI）和结构强度（PSSI）。

美国AASHTO（American Association of State Highway and Transportation Officials，AASHTO）利用PSI评价模型通过对路面平整度的评价反映路面使用性能。PSI模型首先利用专家评分法对路段进行总体评价；然后，对路面进行检测，采集路面数据；最后，利用回归模型得到各参数关系［7］。此外，美国U.S.Army Cops and Engineers则采用另一种思路建立了路面状况评价模型，即利用路面状况指数（Pavement Condition Index，PCI）采用扣分法进行评价［8］。这种方法采用打分的方式对评价指标赋值。通过不同等级道路破损类型及其严重程度倒扣分，获得路段的评价分数，并根据分数等级进行参数设定。这种评价模式得到了较广泛地参考和借鉴。这类方法在进行大规模路面养护评价中更为简洁有效。尽管这种路面评价方法的精度尚显不够，但由于数据获取较为便利，有助于提高养护决策效率。因此，这种方法也更多地在实践中被采用。

2.2 评价模式

本文在PCI指数基础上引入LDR指数（Load-related distress index，LDR）。LDR主要反映由交通负荷引起的路面破损，如裂缝和车辙等。LDR指数主要是针对路面状况进行评价，这种方法比较前述评价方法更为直接，在进行常规养护决策中非常便于操作。此方法在美国弗吉尼亚州等地已经被采用。因此，本文以LDR指数对公路路面状况评价为基础进行公路路面养护决策研究。

对于路面的破损状况，LDR指数采用两个主要指标进行评价，即破损程度和破损密度。其指标评价分三级，共九类路面破损状况，见表1。

表1 LDR指数路面破损状况评价等级

LDR指数的变化范围在0～100之间，采用倒扣分的评价方式。因此，LDR分值越高则表明公路路面状况越好，LDR分值越低则表明公路路面状况越差。对于9种路面破损状况的分值，这里参考美国有关指标进行确定［9］，见表2。

表2 LDR指数路面破损状况评分

3 养护决策

3.1 养护模式

公路路面养护工作根据路面的状况不同，相应采取不同等级的养护作业工程。各国对这类等级划分相似，但也略有差异。我国将路面养护作业工程分为小修保养作业、大中修工程和改建工程等。小修保养以路面预防性养护为主；大中修养护主要是对破损路面的维修；改建工程主要是为改善路况，提高交通效率。国外对这类养护作业工程划分也基本为三类。预防性养护（Preventive Maintenance，PM）主要是保持路况，并主动防止路面破损；修复性养护（Corrective Maintenance，CM）主要对路面特性和结构中存在的问题进行维修完善；恢复性养护（Restorative Maintenance，RM）主要对路面状况不良的路段进行维修使其达到原有的功能和技术标准。

虽然养护模式有一定的区别，但在实际养护预算及决策中均是以此为参考，根据实际路段的路面破损状况、长度和面积等进行工程预算。例如，在一定等级条件下，路段有时不需要进行养护作业；而在其它路面状况下，有时需要进行相应的养护作业工程，路面养护决策见表3。

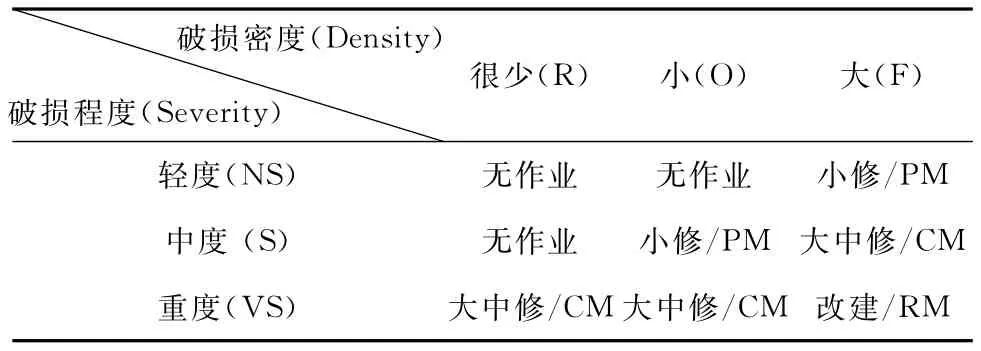
表3 路面养护决策矩阵

3.2 决策模型

公路由于建设标准和工程造价高，路面负荷重，因而使公路养护在管理部门的决策体系中一直处于重要地位。公路作为重要的国有资产，存续时间长，养护内容复杂。因此，本文以年度路面养护决策为例进行研究。由图1可知，公路养护决策是一个循环过程。公路养护决策作为战略性决策，公路管理部门在进行政策制订、体制改革、策略实施过程中均期望这类决策的稳定性要好。也就是说，在决策保持系统性和全面性的条件下，即使出现了比较极端的情况，政策和决策也应是稳定而有效的，这就要求公路的养护决策必须具备较好的鲁棒性。

任何战略决策都以环境条件为前提，公路在养护决策前对养护环境的分析也必须从战略和战术两个层面进行。既要保证养护决策的长期有效，也要确保养护方案具有很强的可行性和可操作性。由于公路养护资源需要量大，特别是在公路养护体制改革未完成的情况下，养护资金总量受限的情况将会持续一段时间。有限的资源必然会面临两类问题：一是资源的有效利用，二是养护资金短缺。因此，公路养护决策模式中养护资源的优化分配就成为主要研究内容。

引起公路路面破损的因素众多复杂，需要进行路面养护的路段分布也存在着随机性。由于公路路面技术等级要求高，往往在某个路段的同一时期内有多处路面需要养护，并且养护的等级和里程也不相同。就某一路段而言，将各破损路面进行统计并汇总分析，可以决定路段的养护作业预算。因此，针对某一路段的养护决策模型为

图1 公路养护决策模式

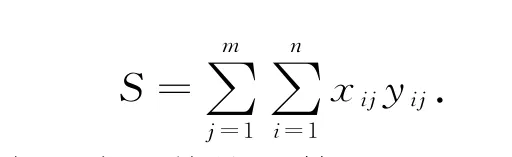
式中：S为路段路面养护预算（万元），xij为第i路段的养护等级为j的单位养护费用（万元／km），yij为第i路段的养护等级为j的养护作业里程（km）。

4 粒子群优化算法（PSO）

公路养护费用高，养护作业规模比较大，作业技术及装备要求高。但是由于公路养护资源有限，导致养护质量和养护规模之间呈现二律背反的现象。因此，公路养护资金的分配也是决策的关键环节。由于对公路路面破损的影响因素来自多个方面，既有系统性因素，也有随机性因素。若采用经验估计等方法可能导致养护预算和实际资金需要量产生较大的差异，所以养护决策模型的优化是解决资金分配问题的关键。本文在以往研究成果的基础上，采用粒子群优化算法（Particle swarm optimization，PSO）拟对公路养护资金模型进行优化分析。

4.1 PSO原理

粒子群优化算法是一种基于群智能（Swarm Intelligence）活动的演化算法（Evolutionary Computation），它也是近年来应用较多的优化工具之一。Eberhart和Kennedy在1995年提出这一优化算法。粒子群优化算法是对鸟群或鱼群等群体动物行为活动模拟而产生的，例如鸟群捕食的群体行为。一般情况下，群体动物会比个体动物表现出更强地处理复杂问题的能力［10］。粒子群优化算法初始为一群随机的粒子（Particle），每个粒子都有自己的位置和飞行速度。粒子群记忆并跟随目前的最优粒子，在空间运动求解。在每一次迭代中，粒子会更新自己的位置，一个是其本身的极值点（Pbest），另一个是群体目前的极值点（Gbest）。

设粒子i的信息以D维向量表示，粒子i的位置和速度分别为：Xi＝（xi1，xi2，…，xiD）T，Vi＝（vi1，vi2，…，viD）T，则粒子i位置和速度的更新公式为

4.2 算法流程

粒子群优化算法的流程可以归纳为以下几个步骤。首先，初始化粒子群的状态，设定粒子的位置和速度，评价每个粒子，确定每个粒子的适应值；进行粒子更新，对每个粒子状态择优；然后，更新全部粒子的位置和速度；检验是否达到结束条件，如达到设定准则，优化结束，获得个体最优适应度值，否则继续迭代计算。

4.3 优化实例

本文以某养护中心为例，以粒子群优化算法对公路路面养护优化进行研究。这里选择10个实验路段。在以往养护决策中，更多地寻求和依靠该路段的历史养护资金数据中存在的规律，并按照路段长度平均分配养护资源。这对不同破损情况的不同路段养护会造成一定的影响，导致资源过剩或不足，不利于有限养护资源的优化利用。因此，采用粒子群优化算法按照实际条件设定约束，仿照实际养护状况寻优，在一定程度上可以防止养护资金分配中过度依赖历史数据，而导致养护资金分配缺乏适度的灵活性。这里使用MATLAB的PSOt（粒子群优化算法工具箱）进行优化计算，以寻求最优解。

该养护中心某路段的年度养护资金见图2。由图可知，通过150次迭代计算，下年度该路段路面养护预算参考值为8.240 31，即在路面养护后其平均技术等级达到小密度轻度破损的水平（无需养护水平）情况下，给予该路段的最大养护资金参数。由该养护资金参考值则可推算出该路段下年度的路面养护资金预算值。

图2 最优适应度值与累积值

5 结束语

本文提出了多种方式对公路养护进行评价的方法，将技术指标评价法和专家评价法较好地结合起来。这有利于对公路养护项目进行分析和决策，

［1］GENDREAU M，SORIANO P.Airport pavement g增强养护决策的可操作性。在综合评价的基础上，提出针对不同路面条件下不同的养护作业决策。最后，利用粒子群优化算法对路段养护决策进行优化试算，从而实现在一定养护目标条件下，路面养护资金的优化运用。

［2］CHAN W T，FWA T F，TAN C Y.Road‐Maintenance Planning Using Genetic Algorithms.I：Formulation［J］.Journal Transportation Engineering，1994，120（5）.

［3］Saeideh allah-Fini，Hazhir Rahmandad，Konstantinos Triantis and Jesus M.de la Garza.Optimizing highway maintenance operations：dynamic considerations［J］.System Dynamics Review，2010（26）.

［4］邹培国.路面养护决策优化技术研究［J］.中国公路学报，1995（2）.

［5］虞安军.高速公路路面养护决策混合遗传优化方法［J］.交通运输工程学报，2007（7）.

［6］刘军，程建川.利用SCE算法进行高速公路路面养护决策优化［J］.交通与计算机，2006（4）：26-29.

［7］AASHTO.Guidelines for Pavement Management Systems［R］.American Association of State Highway and Transportation Officials.Washington D.C.，U.S.A.，1990.

［8］SHAHIN M Y，DARTER M I，KOHN S D.Development of a Pavement Condition Index for Roads and Streets［R］.Interim Report.U.S.A.，1978.

［9］CHOWDHURY T.Supporting Document for Pavement Models and Decision Matrices Development Process Used in the Needs-based Budget［R］.Virginia Department of Transportation Asset Management Division，Richmond，VA，2007.

［10］杨维，李歧强.粒子群优化算法综述［J］.中国工程科学，2004（5）.

［11］EBERHART R C，SHI Y.Particle Swarm Optimization：Developments，Applications and Resources［A］.Proceedings of the IEEE Congress on Evolutionary Computation.Piscataway，NJ：IEEE Service Center，2001.

［责任编辑：郝丽英］

Optimization decision of highway maintenance based on PSO algorithms

LI Yan

（College of Economics and Management，Heilongjiang Institute of Technology，Harbin 150050，China）

It focuses on some problems which are in the highway maintenance management decisions.Taking the pavement maintenance as an example，through LDR indexes，a maintenance decision-making model is established.By using of particle swarm optimization（PSO）decision model，the different pavement conditions of highway maintenance decisions will be optimized.The results of this research will provide some support for highway maintenance decision，and present an optimization methodology for highway maintenance funding.

highway maintenance decision；optimization decision；LDR indexes；particle swarm optimization（PSO）

U418.4

A

1671-4679（2015）01-0047-04

2014-09-09

黑龙江省交通运输厅重点科技项目（JT2011-02GLJ）

李 岩（1972－），男，教授，研究方向：交通运输管理.