Ad hoc网络消息传播过程的高阶描述模型
2015-06-09姚文强朱艳琴李领治
姚文强 杨 哲 朱艳琴 李领治
(苏州大学计算机科学与技术学院,苏州215006)(苏州大学江苏省计算机信息处理技术重点实验室,苏州215006)
Ad hoc网络消息传播过程的高阶描述模型
姚文强 杨 哲 朱艳琴 李领治
(苏州大学计算机科学与技术学院,苏州215006)(苏州大学江苏省计算机信息处理技术重点实验室,苏州215006)
为避免采用随机抽样模型对Ad hoc网络消息传播过程进行定量分析时存在的高估消息覆盖节点数的问题,对现有模型进行修正,提出了一种高阶描述模型.该模型在转发消息时考虑了会对下一次消息转发到达新节点的概率产生影响的2个参数:节点被访问次数和节点度.节点被访问的次数越多,模型的阶数越高.在包含2 000个节点的随机图网络拓扑上的仿真试验结果表明,当消息覆盖的节点数超过1 800时,无论拓扑是否连通,一阶模型和二阶模型对Ad hoc网络消息传播过程的拟合度均优于随机抽样模型.当网络拓扑不连通时,一阶模型和二阶模型仍会高估消息覆盖的节点数;相反,当网络拓扑连通时,两者对仿真结果的拟合度较好,最终误差分别为-7%和-1%.
Ad hoc网络;消息传播过程;节点覆盖;高阶模型
Ad hoc网络是一种自治、多跳系统,每个节点在发送消息的同时,也转发其他节点的消息,以实现资源共享和协作.在Ad hoc网络中进行节点或资源的搜索与定位时,主要通过网络内传播查询消息来完成.节点覆盖问题是指从整体性能的角度,转发尽可能少的消息来覆盖尽可能多的节点[1].由于Ad hoc节点的加入和离开是动态的,因此网络拓扑是动态随机的[2].研究Ad hoc网络消息传播过程时,一般采用随机游走法[3-5]、洪泛法[6]或者其他变异方法[7-12].其中,洪泛法的响应速度最快,但传播开销最大;随机游走法虽然响应速度慢,但在消息覆盖的节点数和传播开销等方面性能较好,是目前主要运用的方法[13].其中,消息覆盖的节点数(即网络中消息经过的节点数量)是一个关键问题.当网络中节点较多且消息经过的节点数较少时,消息传播过程可以用随机抽样模型描述;但随着消息在网络节点间的不断扩散,随机抽样模型会高估消息覆盖的节点数.
本文通过引入节点被访问次数和节点度2个参数,对随机抽样模型进行修正.着重分析了两者对下一次消息转发到达新节点的概率所产生的影响,并推导出相应的计算方法.
1 消息传播过程的随机抽样模型

φ(z)=M(1-e-z/M)
(1)
但消息在Ad hoc网络中的传播过程并不是一个完全独立随机过程[13].消息到达某个节点后,下一跳恰好选择一条新的连接从而到达一个新节点的概率,不仅与当前网络中新节点的个数有关,也与当前节点度及被消息访问的次数有关;而随机抽样模型并不考虑这2个因素.因此,在估计某一时刻Ad hoc网络中消息已覆盖的节点数时,会出现估计值过高的问题.
2 消息传播过程的高阶描述模型
2.1 简单代数模型
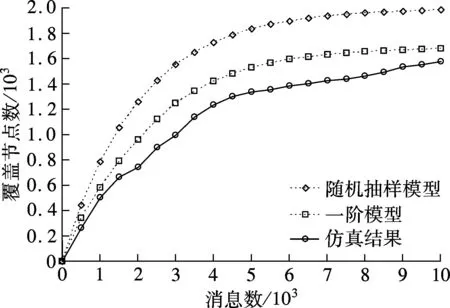
Ad hoc网络拓扑可用随机图G(N,P)表示,共有N个节点,任意2个节点间存在连接的概率为P(0 (2) N趋于无穷大时,可得 (3) 式(3)的解为 (4) 式(4)所示的简单代数模型在计算每次消息转发到达新节点的概率时,都假设其等于未访问节点数和总节点数之比,即[N-u(x)]/N.这种假设只有在消息第1次访问该节点时才成立.当节点已经被访问后,这一概率会下降,下降幅度与节点度有关.节点度越大,消息仍能以较高的概率到达其他新节点.在极端情况下,如果节点被多次访问,所有连接均被遍历后,当消息再次访问该节点时,则不可能经由一条新连接到达其他新的节点.因此,需要对式(4)所示的简单代数模型进行修正,引入节点度和节点被访问次数2个参数,重新计算每次消息转发到达新节点的概率. 2.2 节点度的影响 在式(2)中,当前消息覆盖的节点数为u(x),令p(x)为节点通过一条新连接将消息转发给一个新的邻居节点的概率,则消息转发后覆盖的节点数u(x+1)为 (5) 下面以节点被访问的次数k作为分支条件,讨论节点被访问k次后仍存在新连接的概率pk. 1) 当k=0时,消息首次访问该节点,节点的所有连接都是新连接.此时节点存在新连接的概率为p0=1. 2) 当k=1时,节点的旧连接数L1=2,即一条进一条出,则消息经过新连接被转发的概率为p1=(d-2)/d,其中d为节点度. 3) 当k=2时,节点存在多条旧连接的可能性变得复杂.令wk(i)表示节点被访问k次后拥有i条旧连接的概率,则此时节点存在2,3,4条旧连接的概率w2(2),w2(3),w2(4)分别为 节点被访问过2次后旧连接条数为 L2=2w2(2)+3w2(3)+4w2(4) (6) 节点被访问过2次后,下一次消息转发仍能经过一条新连接到达一个新节点的概率为 (7) 4) 当k=3时,在节点旧连接数为L2的条件下,经过下一轮转发,变成L2,L2+1,L2+2条旧连接的概率分别为 节点被访问过3次后旧连接数为 (8) 同理,节点被访问过3次后,下一次消息转发仍能经过一条新连接到达一个新节点的概率为 (9) 5) 以此类推,当节点被访问过i(i>3)次后,旧连接数为Li-1,经过下一轮转发后变成Li-1,Li-1+1和Li-1+2条旧连接的概率分别为 节点被访问过i次后旧连接条数为 (10) 节点被访问过i次后,下一次消息转发仍能经过一条新连接到达一个新节点的概率为 (11) 2.3 访问次数的影响 式(5)中的p(x)是一个关于x的随机函数,取决于当前节点已经被访问过k次的概率.假设x个消息被转发后覆盖了u个节点,则任一节点被访问k次的概率为 (12) p(x)即可表示为节点被访问次数k与节点存在新连接的概率的加权平均,即 (13) 将式(13)代入式(5),得到如下的高阶描述模型: (14) 模型中的阶数与节点被访问次数k有关. 根据式(12),在节点数为N的网络中,若x个消息被转发后覆盖了u(x)个节点,则qk(x)会随着k的增加而迅速减小.例如,当N=2 000,u=1 000,x=1 386时,对于k=0,1,2,3,4分别有q0(x)=0.499 9,q1(x)=0.346 6,q2(x)=0.120 1,q3(x)=0.027 7,q4(x)=0.004 8.可见,当x≪N时,节点被重复访问2次以上的概率qk(x)(k>2)接近于零.因此,实验中不考虑k>2的情况,仅利用一阶模型(k=1)和二阶模型(k=2)来分析消息传播过程. 基于NS-2 V2.29仿真平台,模拟了包含2 000个节点的网络,网络拓扑服从随机图模型[16].本文仅针对消息传播过程进行研究,因此不考虑消息传输的时延和丢包等情况,所有消息数据包大小为1 B.实验开始时,随机选择1个节点作为消息源,向其邻居节点扩散消息.所有收到消息的节点在1个时钟周期内仅允许转发1次该消息.在每个时钟周期结束后,统计当前消息覆盖的节点数.待节点转发消息的次数累计达到1×104时,实验结束;以10次实验的平均值作为仿真结果. 3.1 一阶模型 当d=4,6,10时, 一阶模型、随机抽样模型及仿真实验得到的消息覆盖节点数对比见图1.由图可知, 一阶模型理论值曲线更接近仿真结果曲线,说明相比随机抽样模型,一阶模型对消息传播过程的拟合度更高. 值得注意的是,当d=4,6时, 一阶模型理论值大于仿真结果,说明随着转发消息数的增加,一阶模型仍会高估消息覆盖的节点数. 这是因为当节点度较小时,图不连通.在包含2 000个节点的随机图网络中,节点度d=P(N-1),当d=4时,P=0.002,当d=6时,p=0.003.PN (a) d=4 (b) d=6 (c) d=10 3.2 二阶模型 由图1(c)可知,当d=10时,随着转发消息数的增加,一阶模型会低估消息覆盖的节点数.这是因为在转发消息数较小时,节点被多次访问的概率较小.然而,当消息数足够大时,节点被多次访问的概率也会变大.因此,可用二阶模型替换一阶模型.二阶模型、随机抽样模型及仿真实验得到的消息覆盖节点数对比见图2. (a) d=4 (b) d=6 (c) d=10 当d=4,6时,二阶模型理论值仍大于仿真结果,这同样是由于网络拓扑的连通性问题引起的.但当d=10时,由于网络是连通的, 二阶模型对仿真结果的拟合程度较一阶模型好,且随着网络中转发消息数的增加,误差会逐渐减小.当消息转发数小于3×103时, 二阶模型理论值与仿真结果的平均拟合误差为12%;当消息转发数达到5×103时,拟合误差为-0.1%;当消息转发数达到1×104时,实验结束,二阶模型的消息覆盖节点数为1 807, 仿真结果为1 828, 拟合误差为-1%. 综上可知,当消息覆盖的节点数超过1 800时,无论拓扑是否连通,一阶模型和二阶模型对Ad hoc网络消息传播过程的拟合度均优于随机抽样模型.当网络拓扑不连通时,一阶模型和二阶模型仍会高估消息覆盖的节点数;当网络拓扑连通时,两者对仿真结果的拟合度较好,最终误差分别为-7%和-1%. 在Ad-hoc等协作通信系统中,消息传播的目的是通过尽可能少的消息来覆盖尽可能多的节点.随着转发消息数的增加,随机抽样模型会高估消息覆盖的节点数.本文提出了一种高阶描述模型.该模型在转发消息时,考虑了节点被访问次数和节点度对下一次消息到达新节点的概率所产生的影响及其程度.通过仿真实验,验证了高阶模型的有效性.由于未考虑网络拓扑的影响,所得结论仅是在随机图网络拓扑上得出的.而在实际应用中,一般网络拓扑更接近小世界网络或幂律网络.这种网络拓扑上消息传播过程的定量分析是今后研究的重点. References) [1]Sun Y, Zhang S K, Xu H L, et al. Cooperative communications for wireless ad hoc and sensor networks [J].InternationalJournalofDistributedSensorNetworks, 2013,2013:161268-1-161268-2. [2]Zhang S K, Fan J X, Jia J C, et al. An efficient clustering algorithm in wireless sensor networks using cooperative communication [J].InternationalJournalofDistributedSensorNetworks, 2012, 2012: 274576-1-274576-11. [3]Dolev S, Schiller E, Welch J. Random walk for self-stabilizing group communication in ad hoc networks [J].IEEETransactionsonMobileComputing, 2006, 5(7): 893-905. [4]Bar-Yossef Z, Friedman R, Kliot G. RaWMS-random walk based lightweight membership service for wireless ad hoc networks [J].ACMTransactionsonComputerSystems, 2008, 26(2):5-1-5-66. [5]Avin C, Krishnamachari B. The power of choice in random walks: an empirical study [J].ComputerNetworks, 2008, 52(1): 44-60. [6]Chang N B, Liu M. Optimal controlled flooding search in large wireless networks [C]//Proceedingsof3rdInternationalSymposiumonModelingandOptimizationinMobile,AdHoc,andWirelessNetworks. Trentino, Italy, 2005: 229-237. [7]Jiang S, Guo L, Zhang X D, et al. Lightflood: minimizing redundant messages and maximizing scope of peer-to-peer search [J].IEEETransactionsonParallelandDistributedSystems, 2008, 19(5): 601-614. [8]Elsässer R, Sauerwald T. Tight bounds for the cover time of multiple random walks [J].TheoreticalComputerScience, 2011, 412(24): 2623-2641. [9]Beraldi R. Biased random walks in uniform wireless networks [J].IEEETransactionsonMobileComputing, 2009, 8(4): 500-513. [10]Zuniga M, Avin C, Krishnamachari B. Using heterogeneity to enhance random walk-based queries [J].JournalofSignalProcessingSystems, 2009, 57(3): 401-414. [11]Bisnik N, Abouzeid A A. Optimizing random walk search algorithms in P2P networks [J].ComputerNetworks, 2007, 51(6): 1499-1514. [12]Rodero-Merino L, Anta A F, López L, et al. Performance of random walks in one-hop replication networks [J].ComputerNetworks, 2010, 54(5): 781-796. [13]Kang C. Survey of search and optimization of P2P networks [J].Peer-to-PeerNetworkingandApplications, 2011, 4(3): 211-218. [14]Xie J, Lui K S. Modeling random walk search algorithms in unstructured P2P networks with social information [C]//Proceedingsof2009IEEEInternationalConferenceonCommunications. Dresden, Germany, 2009: 1-5. [15]López Millán V M, Cholvi V, López L, et al. A model of self-avoiding random walks for searching complex networks [J].Networks, 2012, 60(2): 71-85. [16]Erdös P, Rényi A. On the evolution of random graphs [J].PublicationoftheMathematicalInstituteoftheHungarianAcademySciences, 1960, 5: 17-61. High-order description model of message propagation process in Ad hoc network Yao Wenqiang Yang Zhe Zhu Yanqin Li Lingzhi (School of Computer Science and Technology, Soochow University, Suzhou 215006, China) (Provincial Key Laboratory for Computer Information Processing Technology, Soochow University, Suzhou 215006, China) To avoid the overestimation problem of the number of nodes covered during the quantitative analysis of message propagation process in Ad hoc network by using the random sampling model, a high-order description model is proposed by modification. In the proposed model, when the message is transmitted, the visit times and the degrees of nodes which influence the probability of the next messages transmitted to new nodes are considered. The more the visit times, the higher the order of the description model. The simulation results on a random graph topology network with 2 000 nodes show that when the number of nodes covered is more than 1 800, the fitting abilities of both the 1-order model and the 2-order model for the message propagation process in Ad hoc network are better than that of the random sampling model whether the network topology is connected or not. When the network topology is disconnected, both the 1-order model and the 2-order model still overestimate the number nodes covered; on the contrary, when the network topology is connected, the fitting degrees of both the 1-order model and the 2-order model for the simulation results are satisfactory, and the final fitting errors are -7% and -1%, respectively. Ad hoc network; message propagation process; node coverage; high-order model 10.3969/j.issn.1001-0505.2015.03.003 2014-11-13. 作者简介: 姚文强(1992—),男,硕士生;杨哲(联系人),男,博士,副教授,yangzhe@suda.edu.cn. 国家自然科学基金资助项目(61373164)、江苏省产学研前瞻性研究计划资助项目(BY2013030-06)、苏州市科技计划资助项目(SYG201238, SZS0805). 姚文强,杨哲,朱艳琴,等.Ad hoc网络消息传播过程的高阶描述模型[J].东南大学学报:自然科学版,2015,45(3):428-432. 10.3969/j.issn.1001-0505.2015.03.003 TP393 A 1001-0505(2015)03-0428-05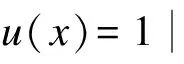
3 实验结果与分析





4 结语
