光笔式双目视觉测量系统标定技术研究

熊 鑫，孙冬梅，范 文，徐海鹏

(南京工业大学 自动化与电气工程学院，江苏 南京 211816)



光笔式双目视觉测量系统标定技术研究

熊 鑫，孙冬梅，范 文，徐海鹏

(南京工业大学 自动化与电气工程学院，江苏 南京 211816)

针对光笔式双目视觉测量系统的标定问题，讨论了关于相机内参、双相机外参以及测量笔的相关标定理论,开发了一整套基于LabVIEW的标定系统。运用张氏平面标定法实现了相机内参标定。结合基于标准长度的外部参数标定方法，实现了双相机外参数标定。运用粒子群算法和LM算法相结合，加快了目标函数高维寻优速度。在测量笔标定环节，提出了一种基于最小二乘法的现场校准方法。标定系统完成了后期开展相关测量前的所有准备工作，具有较高的精度和实用性。在测量系统标定结果基础上对直径25 mm标准陶瓷球进行测量，测量结果标准差达到0.019 mm。

双目视觉；标定；外部参数；内部参数；粒子群算法；LM算法

引言

随着工业测量技术的发展，三坐标测量的要求也越来越高[1]。光笔式双目视觉测量系统采用2台位置相对固定的CCD摄像机同时拍摄测量笔面板图像，通过提取测量笔面板的特征点的图像坐标，从而实现三维空间坐标的测量。它是一种非接触传感的测量方法。

为了获得高精度的三维空间坐标，必须对影响系统精度的关键技术进行研究[2]。其中系统的标定技术最为关键，直接决定着三维重建以及测量的精度。标定技术包含相机内部参数标定，双相机外部参数标定以及测量笔标定[3-4]。

近年来，基于双目视觉的三坐标测量系统得到了迅速的发展，如挪威Metronor公司的DCS系统和瑞士Lecia公司的V-STARS/M系统以及哈尔滨工业大学的实验样机等。已知特征点的图像坐标求取摄像机内部参数，国内外学者已经提出了许多标定方法，如透视变换法、双平面法、Tsai两步法等[5-7]。但目前国内对于整个光笔式双目视觉测量系统的标定文献比较少，开发出一整套能运用于现场灵活校准的标定系统显得尤为重要。

本文针对2台CCD相机的内部参数标定问题，采用了张正友法实现了校准。在2个相机内参分别标定完成的基础上，搭建了双目视觉测量模型，构建了2个相机图像坐标与世界坐标间的关系。以二维十字标定靶特征点的标准长度为基准，结合粒子群算法和LM迭代算法，最小化标靶特征点间长度实际值与计算值之间的误差平方和，实现对2个相机外部参数的标定和优化。基于最小二乘方法，实现了测量笔测尖的现场校准。本文开发的一整套标定系统，为后期进行高精度坐标测量奠定了基础，实用价值高。

1 相机内参数标定

精确校准2个相机的内部参数，可以减小其对系统测量精度的影响。由相机小孔透视模型可得到：

zm=P[R,T]M

(1)

式中：m=[u,v,1]T，为计算机图像坐标系下的坐标齐次形式；M=[X,Y,Z,I]T，为世界坐标系下的坐标齐次形式；T为世界坐标系原点到相机光心矢量；P为内参数矩阵，即

(2)

式中：(u0,v0)为像主点坐标；fx和fy分别为u、v轴的尺度因子；μ为畸变因子。确定矩阵P的过程即相机内参数标定。

张正友提出了采用平面模板标定的方法[5]，利用相机对标定模板不同方位拍摄，从而实现相机标定。避免了传统标定方法繁琐的缺点，又比自标定方法精度好。令标定靶平面Z坐标为0，R=(r1,r2,r3)，则(1)式可改写为

(3)

图像点m与标定靶上点M存在一个变换H:

zm=HM

(4)

记H=(h1,h2,h3)，有

(h1,h2,h3)=λP(r1,r2,T)

(5)

由于P的行列式不为0，所以det[H]≠0。由旋转矩阵的正交性，可得

(6)

(6)式为摄像机内参数矩阵2个基本约束。

(7)

因为B对称，可表示为

b=[B11,B12,B22,B13,B23,B33]

(8)

H中第i列向量为

hi=[hi1,hi2,hi3]T

(9)

vij= [hi1hj1,hi1hj2+hi2hj1,hi2hj2，hi3hj1+

hi1hj3,hi3hj2+hi2hj3,hi3hj3]

(10)

可以得到b为未知数的齐次方程：

(11)

对不同位置的标定靶平面拍摄n张照片，标定靶位置尽量布满整个视场空间。将n个(11)式这样方程叠加起来，可得:

Vb=0

(12)

V是2n×6的矩阵。若n>2，可求得b的唯一解。根据求得B可求解内参数矩阵P。其中

(13)

2 双相机外参数标定

2.1 双目视觉测量模型

一般情况，双目立体视觉测量对于2个相机摆放没有特别要求，如图1所示。

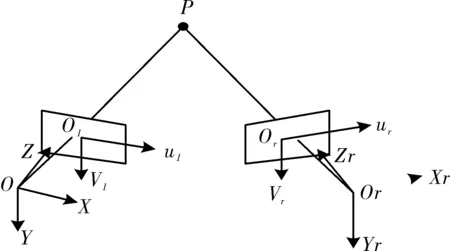
图1 双目立体视觉测量中空间点三维重建Fig.1 Space point 3D reconstruction in binocular stereo vision measurement

令左相机光学中心位于世界坐标系O-XYZ原点，且无旋转。左相机图像坐标系O1-u1vl，有效焦距为fl。右相机的坐标系为Or-XrYrZr，图像坐标系为Or-urvr，有效焦距fr。

左相机坐标系O-XYZ与右相机坐标系Or-XrYrZr之间的相互位置关系可以用矩阵M表示成：

M=[R,T]

(14)

式中：R为左右2个相机坐标系之间的旋转矩阵；T为右相机坐标系相对于左坐标系原点之间的平移矢量。

2个相机视场中的三维坐标可以表示成：

(15)

由(15)式可以看出，已知左右相机的焦距和空间点在2个相机中图像坐标，只要求出旋转矩阵R和平移矩阵T，就可以求出空间点的三维空间坐标值[8]。

2.2 外参数标定理论与方法

外部参数标定是指在摄像机内部参数确定后，确定视觉系统的结构参数R和T。本文采用基于标准长度的标定方法。所用标靶如图2所示。为了提高标定精度，采用的十字标定靶已经精密校准，特征点1到5之间距离为定值。D3j(j=1,2,4,5)为十字标靶上j点到3号点的实际精确距离。其中D31=200.234 157 1，D32=199.787 142 4，D34=199.682 366 4，D35=200.283 831 8。

图2 十字形标靶Fig.2 Calibration cross

引入加强目标约束函数：

(16)

式中：D(pi3,pi j)是摄像机第i次同步拍照，计算出的3号点到j号点的距离。通过最小化距离的计算值与实际值的误差平方和，可以校准外部参数R和T[9]。从而可以构建无约束优化目标函数为

(17)

外部参数标定步骤如下：

步骤1) 2个相机同步拍摄6次十字标定靶图像(左右相机分别为6幅)，读入图像，利用数字图像处理的相关方法，实现5个特征圆点的中心图像坐标提取，作为标定的特征点。

步骤2) 利用粒子群算法将相机的12个外部参数作为算法中的12个粒子。(17)式中目标函数作为适应度函数。利用粒子群算法最小化式中的目标函数，从而得到全局最优解：

gBest=[r1,r2,r3,r4,r5,r6,r7,r8,r9tx,ty,tz]T

(18)

算法实现步骤如图3所示。

图3 粒子群算法实现流程Fig.3 Flow chart of particle swarm optimization

步骤3) 将求得的外参初值作为(17)式无约束优化迭代初值，利用LabVIEW自带的非线性优化工具，实现外部参数的LM迭代优化。

3 测量笔标定

因测量笔的测尖预校准以及测头更换过程很难避免一些不确定性因素[10]。每次测量前必须对测尖坐标进行精确标定，减小其对整个系统精度影响。

将测尖处小球固定在相同半径的球形座内，如图4所示，测量笔在一定锥角内任意摆动并采集图像。笔尖位置固定，笔身位置改变。假设测量笔坐标系OXpYpZp的原点在测笔坐标系下坐标Op，在世界坐标系下坐标Ow。测量笔测尖在测笔坐标系下坐标为Tp，在世界坐标系下坐标为Tw。因为标定座固定不动，所以每次成像时Tw为常量。

图4 测笔标定示意图Fig.4 Schematic diagram of measurement pen calibration

假设测量笔在位置1，世界坐标系与测笔坐标系之间的转换关系有

Op=R1Ow1+T1

Tp=R1Tw+T1

(19)

Tp-Op表示测尖到测量笔原点间距离，因为距离为常量，记为C。因此

(R1Tw+T1)-(R1Ow1+T1)=C

(20)

整理(20)式，可得

R1Tw-R1Ow1=C

(21)

晃动测量笔，在位置2采集图像时

R2Tw-R2Ow2=C

(22)

同理，在位置n时有

RnTw-RnOwn=C

(23)

根据 (21)式和(22)式，可推得

(R2-R1)Tw=R2Ow2-R1Ow1

(24)

以此类推，可以得到第n次和第n-1次的关系为

(Rn-Rn-1)Tw=RnOwn-RnOw(n-1)

(25)

任意摆动测量笔采集n次图像，由(25)式构成一个Tw的方程组:

(26)

该方程组可以通过最小二乘方法求解，确定测尖在世界坐标系下坐标Tw为

Tw=(QTQ)-1QTb

(27)

根据(28)式，可计算出第i次摆动测量笔时，测尖在测量笔坐标系下的坐标Tp i。进而求平均值作为测尖在测笔坐标系下的坐标Tp。

Tpi=RiTw+Ti

(28)

4 实验与标定结果

实验采用2台型号相同的CCD相机进行标定实验。相机型号为：BaslerPIA2400-17GM，分辨率为2 448pixel×2 050pixel。

4.1 内参数标定实验与结果

实验采用7×7圆阵列标定靶，以圆的中心作为标定特征点。采集图像时让标定靶尽量充满整个空间，左右相机共采集16幅图像，其中4幅如图5所示。2台Basler相机内参数标定结果如表1所示。

图5 不同位置平面标定靶图Fig.5 Plane calibration target figures of different locations

表1 摄像机内部参数

4.2 外参数标定实验和结果

由粒子群算法得到外参初始值,如表2所示。采用LabVIEW自带的非线性优化函数工具，对外参数进行进一步LM迭代优化。优化函数如图6所示。其中

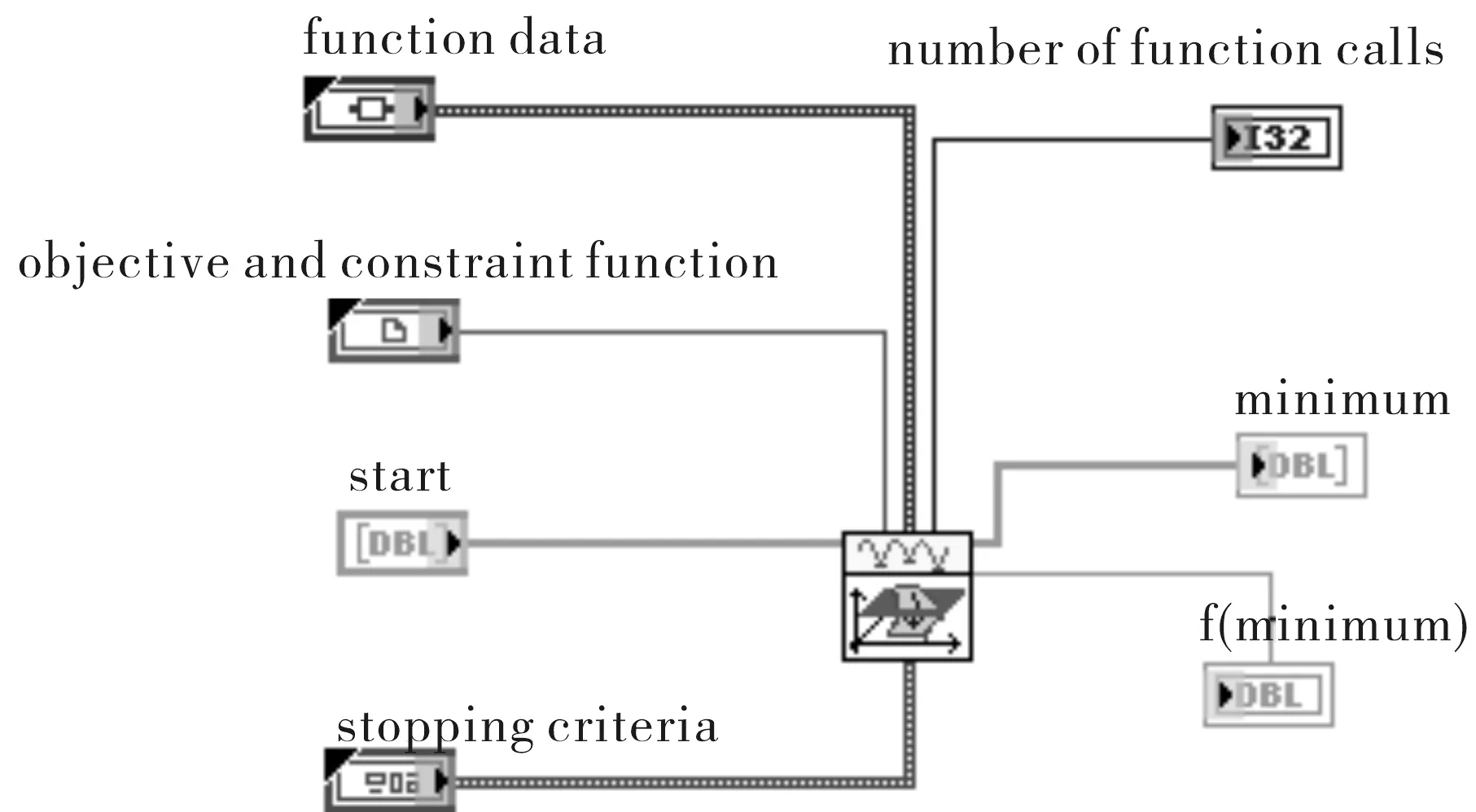
图6 约束优化工具Fig.6 Constrained optimization tool

1) function data为目标函数的静态参数。包含左右相机的焦距以及拍摄的目标物体的左右相机的图像坐标。

2) objective and constraint function为优化求解的目标函数。本文目标函数即(17)式：

3) start为n维初始点。将12个需要标定的外参数作为粒子群算法的12个粒子，用粒子群算法最小化式中目标函数，即初始值R0和T0。

4) stopping criteria为约束优化终止条件的集合。集合包含函数容差：1e-8;参数容差：0.000 1；最大循环次数：5 000；梯度容差：1e-8；最多调用函数次数：30 000。

5) number of function calls是优化过程迭代的次数。最终迭代次数为354次。

6) f(minimum)为目标函数达到的最小值。标定结束后得到的值为79.425 4。

7) minumum为迭代结束最小值处对应的取值点。即所求的12个外参数优化值。

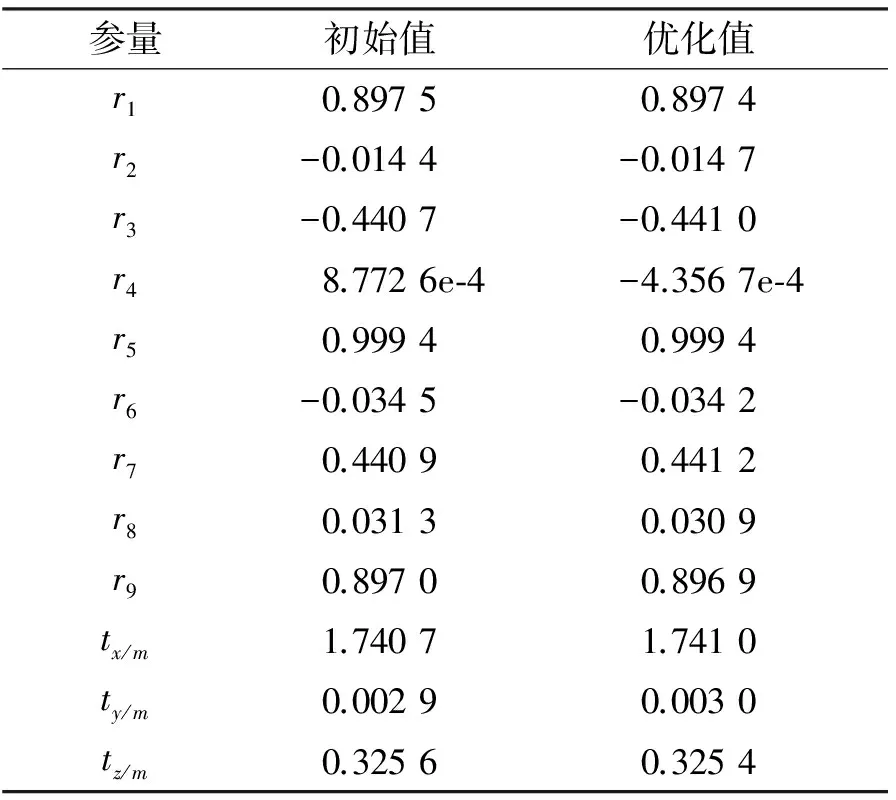
表2 外参数标定结果

4.3 测量笔标定实验和结果

如图4所示，测量笔在制作过程中，9个光学特征点的中心坐标已精确校准。9个圆特征点中心在测量笔坐标系下坐标如表3所示。

表3 测量笔9个特征点的坐标 mm

测量笔放置在标定座上，运行标定程序，拍摄至少6幅以上图像，其中4幅图如图7所示。实验得到测尖标定值为(184.790，-20.459 8，3.248 27)。

图7 测量笔标定部分图Fig.7 Part of measuring pen calibration images

4.4 标准陶瓷球测量实验

将标定后的系统对标准25 mm直径的陶瓷球测量进行验证。固定相机坐标系，将陶瓷球固定在相机视场范围内。用测笔去测球上任意的点的坐标。每次测量球上任意20点，共测10组。通过拟合每组测量点，得出拟合直径如表4所示。

表4 直径25 mm标准陶瓷球测量值 mm

Table 4 Measured values for standard ceramic ball with 25 mm diameter

序号测量值绝对误差125．020．02225．010．01324．990．01425．020．02524．980．02625．030．03725．020．02825．030．03924．990．011024．980．02平均值/标准差25．0110．019

测量结果的平均值为25.011 mm，具有0.011 mm的偏差。测量实验的精度不仅与标定精度相关，还与图像噪声、测量过程中手的抖动等因素有关。会出现绝对误差略微偏大情况，如第6次和第8次测量。测量结果标准差为0.019 mm，结果表明系统总体具有良好的稳定性和可靠性。

5 总结

根据所研究的相关理论，本文采用LabVIEW编写了一整套标定软件。内参标定运用张正友法得到了实现。采用粒子群与LM迭代算法相结合的方法进行外参标定，较传统标定模型精度和速度均有所提高，并且无需预标定，方法简便。采用基于标准长度构造优化的目标函数，加强了模型内部强度，算法精度得到进一步提高。最后将测量笔的测尖固定在空间一点，结合最小二乘方法，实现了测量笔的标定，该方法简便易操作，在每次测量前可以精确校准测头。整套标定系统为后期数据测量提供了良好的基础，具有较高的应用价值。

[1] Zhang Guoxiong. The development trend of three coordinate measuring machine[J].China Mechanical Engineering, 2000，11(1):222-226. 张国雄.三坐标测量机的发展趋势[J].中国机械工程，2000，11(1):222-226.

[2] Jiang Guangwen, Chao Zhichao, Fu Sihua,et al. High accurate camera calibration technique based on controllable rotation[J]. Acta Optica Sinica，2010,30(4)：1309-1314. 姜广文，晁志超，伏思华，等. 基于可控旋转的相机高精度标定技术[J]. 光学学报，2010,30(4)：1309-1314.

[3] Liu Yiyu. Light pen binocular vision measurement system research[D]. Changsha:Central South University,2010. 刘一宇.光笔双目视觉测量系统的研究[D].长沙：中南大学, 2010.

[4] Xu Qiaoyu.Study of the key technologies of online 3D vision measurement system for large-scale equipments[D]. Harbin:Harbin Institute of Technology,2007. 徐巧玉.大型装备在线三维视觉测量系统关键技术研究[D].哈尔滨:哈尔滨工业大学,2007.

[5] Zhang Z Y. A flexible new technique for camera calibration[J]. IEEE Trans. on Patern Analysis and Machine Intelligence, 2000,22(11):1330-1334.

[6] Tasi R Y. An efficient and accurate camera calibration technique for 3D machine vision[J]. Proc. of IEEE Conference of Computer Vision and Pattern Recognition, 1986, 10(3): 364-374.

[7] Wei G Q, Ma S D. Implicit and explicit camera calibration:Theory and experiment[J]. IEEE Trans. on Pattern Recognition and Machine Intelligence, 1994, 16(5): 469-480.

[8] Zhang Guangjun. Visual measurement[M].Beijing:Science Press,2008. 张广军. 视觉测量[M]. 北京：科学出版社，2008.

[9] Xie Kexin. Optimization method[M]. Rev. ed. Tianjin：Tianjin University Press，1997:144-165. 解可新. 最优化方法[M]. 修订版.天津：天津大学出版社，1997:144-165.

[10]Xu Tingfa. Precise perimeter measurement for 3D object with a light-pen vision measurement system [J]. Optics&Laser Technology,2009,41:815-819.

Calibration technique of binocular vision measurementsystem using light pen

Xiong Xin，Sun Dongmei，Fan Wen，Xu Haipeng

(School of Automation & Electrical Engineering, Nanjing University of Technology, Nanjing 211816, China)

Aiming at the calibration problem of the binocular vision measurement system using a light pen, the theory about the calibration of camera intrinsic parameters, double-camera extrinsic parameters and measuring pen was discussed. At the same time, the whole calibration system based on LabVIEW was developed. The camera intrinsic parameters calibration wasachieved by using Zhang plane calibration method,while the double-camera extrinsic parameters calibration was achieved by the method based on standard length. Using the method combining the particle swarm optimization with the Levenberg-Marquard(LM) algorithm, the high-dimensional optimization target function was speeded up effectively. In the process of measuring pen calibration, a very convenient field calibration method based on least square was proposed. The calibration system could complete all the preparation work before the relevant measurement. It has high precision and practicability. Based on the calibration results of measurement system, the standard deviation of test result for the 25 mm diameter standard ceramic ball is 0.019 mm.

binocular vision;calibration; extrinsic parameters; intrinsic parameters；particle swarm optimization; LM algorithm

1002-2082(2015)05-0784-07

2015-04-13；

2015-05-11

江苏省人事厅江苏省博士后资助计划(1201012C)

熊鑫(1991-)，男，江苏常州人，硕士研究生，主要从事视觉测量研究。E-mail：649271900@qq.com

TN911.73;TP27

A

10.5768/JAO201536.0503004