空间多普勒激光雷达海表面散射信号分析
2015-06-09李志刚田茂彬朱林伟
李志刚,田茂彬,朱林伟
(鲁东大学 物理与光电工程学院,山东 烟台264000)
空间多普勒激光雷达海表面散射信号分析
李志刚,田茂彬,朱林伟
(鲁东大学 物理与光电工程学院,山东 烟台264000)
为了验证受海表面风速驱动的海表面反射率模型和计算海表面信号进行零风速校准的精度,开展了激光雷达海表面散射信号强度和速度特征的分析。在强度特征信息方面,进行了海表面反射率仿真模型和机载激光雷达海面散射信号实测数据的对比,考虑激光水下散射,参考QuikSCAT的海表面风速大小,测量结果和模型曲线基本吻合。在速度特征方面,通过海表面运动波形的仿真和海表面速度信息的提取,考虑波面的垂直和水平运动,采用时间积分的海表面探测信号零风速校准误差小于0.2 m/s。
多普勒激光雷达;海表面散射;零风速校准;波面运动
引言
测风激光雷达依其高时空分辨和高精度的探测优势,已经成为测风领域的发展方向,为了提高探测空间覆盖率,车载、机载和星载探测系统应运产生,国际上不断出现研制成功的测风激光雷达系统,主要分为2大类:相干探测激光雷达系统和直接探测激光雷达系统。相干探测只能应用于大气中气溶胶散射的窄线宽信号,对于瑞利散射信号却无能为力,因此只适用于低空测量,而直接探测系统可以同时测量大气中的气溶胶散射和分子散射信号,在适用性上得到了大大的提高。两种探测技术实现了高低空测量的有效结合,多普勒激光雷达也逐步发展成为测风激光雷达系统的发展方向,包括机载/星载探测系统。从国际发展趋势上看,基于车载、机载的测风激光雷达系统取得了很大的进步,为了提高全球的风场观测能力,星载测风激光雷达已经成为下一阶段的发展目标。欧空局ADM-Aelous计划便是国际上首次星载直接探测测风激光雷达的尝试,目标是提供全球的风廓线测量以及气溶胶和云的研究[1-3]。
机载和星载多普勒大气激光雷达的发展应用,解决了空间激光雷达对大气的测量,获取的数据信息不仅仅包括大气的测量信息,同时也获取了地面和海表面的反射信号。鉴于地面和海面不同的反射理论,开展其相应的研究,对于校正机载和星载系统具有重要的研究意义[4-6],也可利用现有系统开展空间多普勒激光雷达辅助产品的应用开发。对于空间多普勒激光雷达系统来说,激光海表面的回波信息已经被公认为系统校准的重要手段之一。本文对海表面散射信号的强度和速度信息进行了分析和计算,并利用机载激光雷达实测数据进行了对比。
1 海面散射信号的获取
机载或星载激光雷达的测量获取了从空间高度到地面的数据廓线,地表散射会出现强散射回波,因此地面和海表散射信号的获取可以用于激光雷达系统数据校正或验证算法中。空间探测示意图如图1所示。
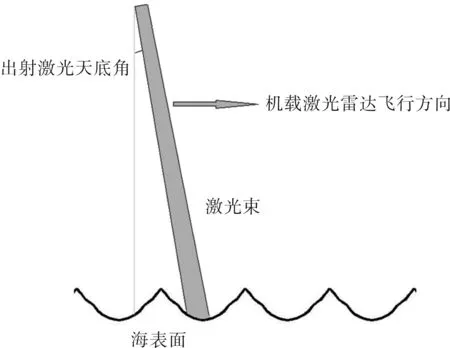
图1 激光雷达地面/海表面测量示意图Fig.1 Sketch map of measurment of land/sea surface by airborne lidar
激光雷达回波接收的信号如图2(a)所示, 横坐标为CCD探测的信号强度,单位LSB表示探测器模数转化的量化间隔,纵坐标为数据廓线的25个存储单元层(仅显示了第8~24层),每个探测单元层由积分时间决定的距离分辨率为315 m。海面散射信号通常不仅仅包含在一个数据点里面,海表面散射信号(G1,G2层)相对于大气信号(G1层以上)要强很多,数据廓线的强度梯度对于大气信号表现出较弱的高度依赖性,但对海表面回波却表现出了极大和极小值,因此,可以利用梯度结果设定甄别阈值来确定地面信号的位置,甄别阈值根据地面信号和大气信号的相对大小自动设定。数据梯度G定义如下:
(1)
式中:zn为第n层探测数据的海拔高度;I(zn)是在高度为zn信号层的强度;θ是天底角;Δr是激光雷达的距离分辨率。梯度廓线计算结果如图2(b)所示,海表面散射信号导致非常大的梯度变化。通过自动阈值计算(通常选为最大梯度值的1/10),提取海面散射信号的位置,对应为数据的第14~15层。激光雷达一般采用积分测量,海面信号存在多层特征,在确定含有地面散射信号的位置后,可以直接进行强度相加,用来代表海表面散射信号强度,背景噪声的滤出可以采用海面散射信号后面的远端信号(如第17~24层)平均值。
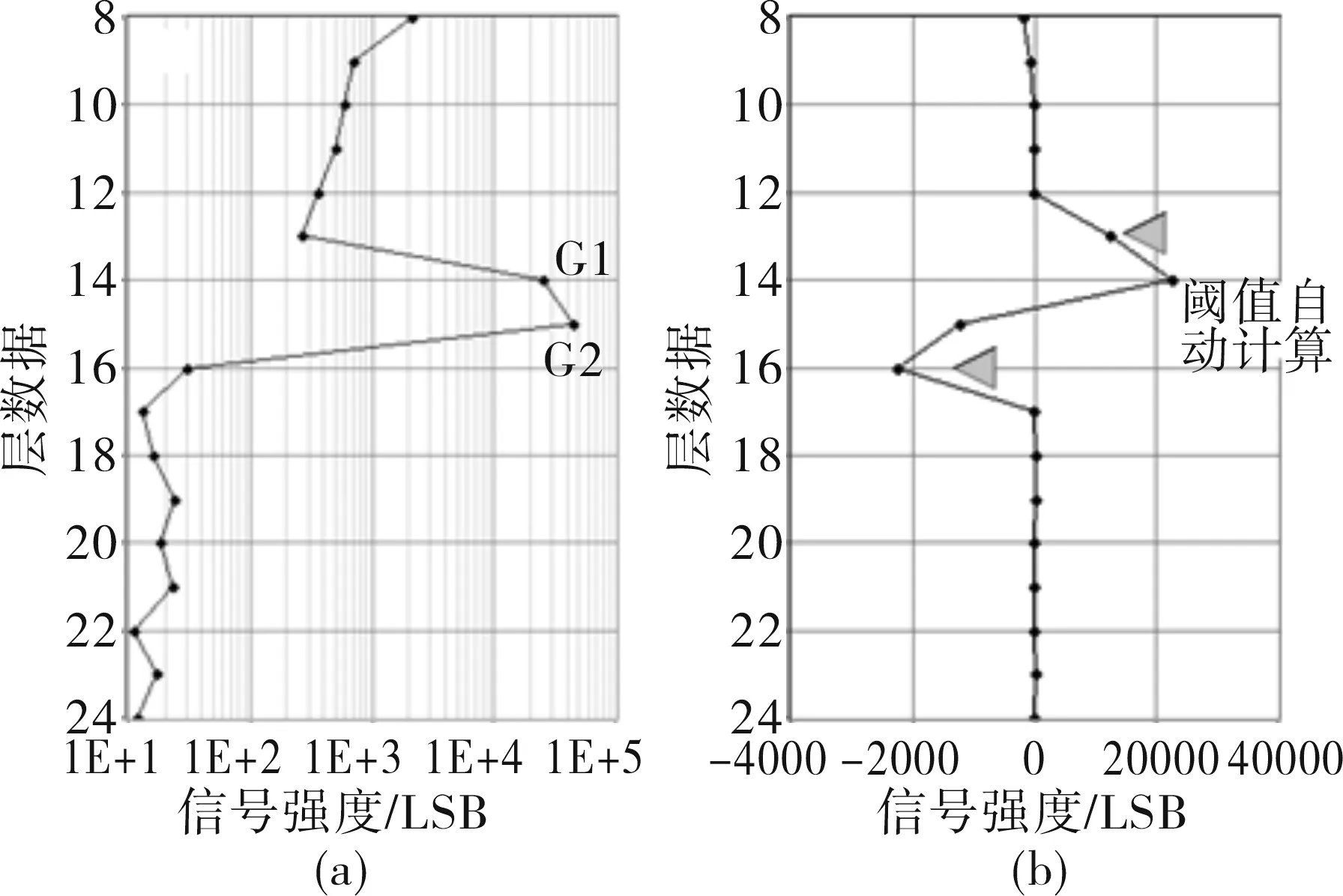
图2 激光雷达回波信号廓线及海表面梯度信号提取回波层Fig.2 Signal profile of lidar and extraction of sea surface signal positions
2 海面散射信号的强度特征分析
海表面在风的驱动下变成为一个非常复杂的运动体,产生许多高低不等、长短不齐的不规则波动, 形成了不同的斜率分布,同时波面的运动产生了海面白帽、气泡等,激光入射到海面上不仅会产生光谱反射,也会产生受海表面风驱动的海面白帽的漫散射。当激光波长大于700nm时,因为海水对激光具有较强的吸收特性,来自水下的激光散射贡献可以被忽略,但是处在可见和UV波段的激光水下散射将产生一定的散射贡献。
机载/星载激光雷达的应用,可以获取不同出射天底角的海表面测量信号,为实验测量不同入射天底角的海表面反射率提供了方法。在确定海表面斜率分布的基础上,模拟仿真不同海表面风速条件下光谱反射率,结合实验数据可以对比分析海面散射信号的强度特征[7-8]。
综合考虑海面的白帽反射、光谱反射和水下散射贡献[9],得到比较完整的海表面的反射率模型,海表面反射率模型共有3个部分组成:海表面白帽反射率、海表面的光谱反射率及来自水下的激光散射贡献。来自这3部分的海表面反射率模型[10]可以写为
(2)
式中:R为海表面反射率,与入射角θ有关;第1项为白帽的反射率,白帽是深海中因风吹拂海浪波顶,使波顶水粒跳出溢出白色的水泡,2个参量决定了海面的白帽反射率:覆盖率W,有效反射率Rwc,eff,白帽覆盖率W是一个由海表风速决定的函数。第2项为发生在没有被白帽覆盖的海面区域的光谱反射率,ρ 是激光的菲涅耳反射率,σ2是海表的波面斜率分布,它是海表风速的函数。第3项为来自水下的激光散射贡献,一种等效的看法就是发生在海表面的等效朗伯反射,R0定义为等效的反射率,0的含义就是利用海面0m深度的朗伯反射代表所有水下的激光散射贡献[9]。
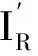
(3)
式中:Iato(n-1)为海表面上层大气散射的信号强度;Iss(n)为海表面散射信号的强度,n为最上层的海表面信号层数。
图3所示给出了A2D激光雷达在2009年9月份的飞行试验——海表面测量信号相对强度与模型曲线的对比结果。通过改变飞机的翻滚角度,实现了5°~40°范围内5个不同天底角的海表面散射信号的测量,实虚线为海表面反射率模型在不同海表面风速条件下的模型曲线,黑色点为激光雷达海表面提取的相对强度信号,在18m/s~19m/s的理论海表风速条件下,两者吻合较好,参考QuikSCAT海表风场,当时的海表风速约为20m/s,因此,在考虑了水下散射贡献的情况下,两者的吻合体现了海表面风速的大小,试验印证了海表面反射率模型。
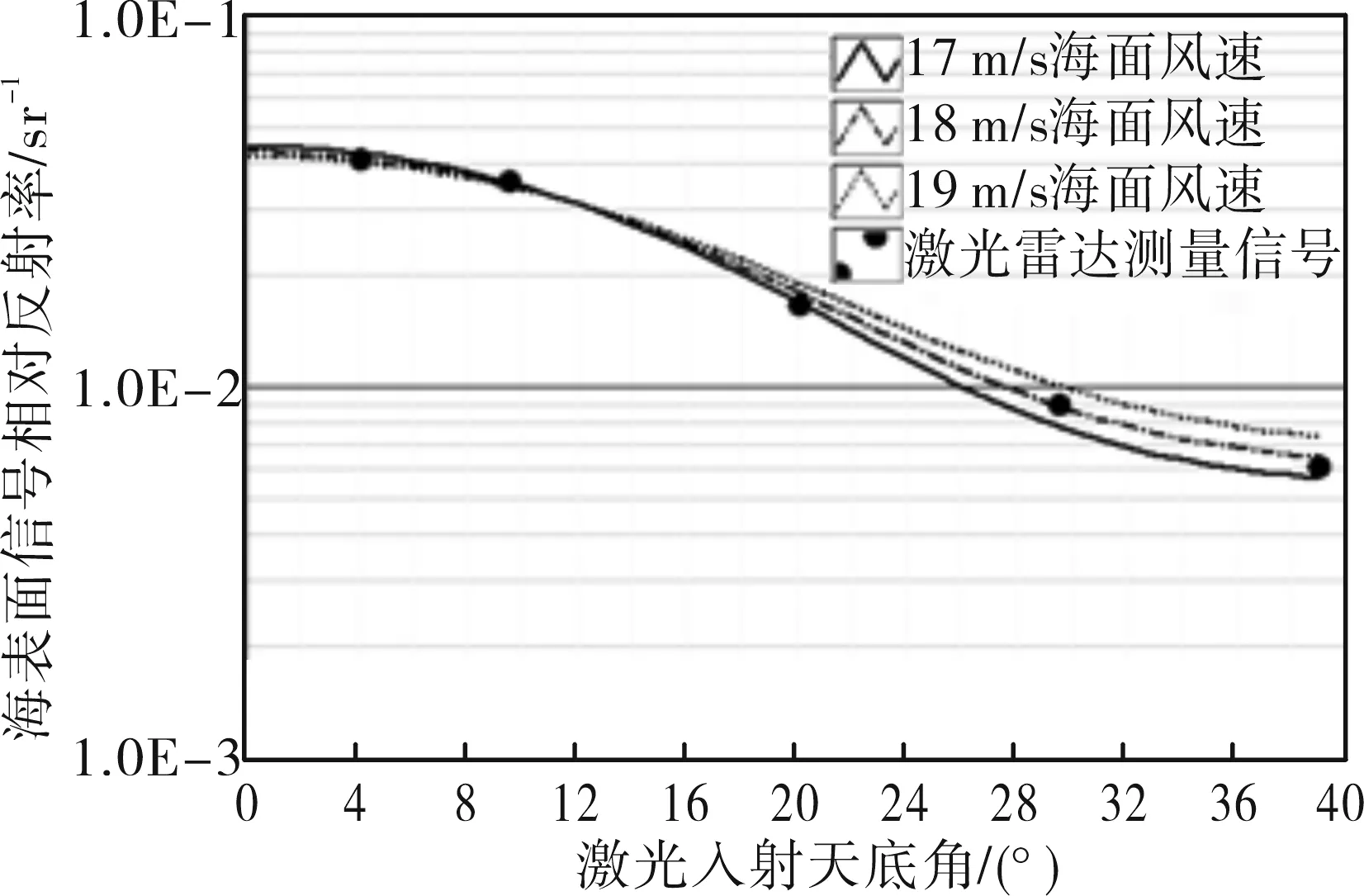
图3 海表面反射率的对比结果(模型曲线的海表面风速:17 m/s~19m/s)Fig.3 Comparison of sea surface reflectance between measurement and models (sea surface windspeed used in model: 17 m/s~19m/s)
3 海表面散射信号的多普勒特征分析
海表面风速会引起激光海表面反射率大小的变化,同样也会引起海表面波面运动的强烈变化。对于机载多普勒激光雷达,由于载体的摇摆和航行会引起测量信号的多普勒频移,而这个速度影响会叠加在测量到的大气径向风速之上,如果不能很好地给以校正(零风速校准),这将使激光雷达系统无法准确获得大气的风场。地面、海面相对于激光雷达对系统来说是静止不动的,这为零风速的修正算法提供了新的手段。与地面散射信号明显不同,海表面风速的变化会引起海表面波面运动的变化,那么波面的运动速度会附加在测量的激光径向速度上,如图1所示,计算该数值的大小需从与海表面风速关联的海表面波形入手,模拟分析海表面运动引起的激光多普勒信息。
为了精细地体现海表面波面的运动,采用车轮状的波形运动,小振幅运动接近于正弦形状,大振幅表现为陡峭变化[11]。在该模型中存在3个变量:h,v,k,分别代表海表面的水平方向、竖直方向和位置点。海表面的运动被表现为一个半径为R的转轮沿着海面上的直线在转动。海表面的位置坐标可以表现为
h(k)=kL-Asin(ωt+2πk)
v(k)=Acos(ωt+2πk)
(4)
式中:ω是轮子的角转动频率;波长L和周期T依赖于波的速度V;g为重力加速度;其表达式如下:
(5)
在该模型中,不仅需要知道海面的波形,还需要计算海面所有点的速度场,海表面波面运动的速度可以求解为
(6)
这样的波面运动体现了固定点的水平速度和垂直速度,实际情况下海表面波面运动还体现了海表面风推动海面波的整体漂流速度,通常被定义为
(7)
该参量与海表面风速没有直接的关联,但是依赖于波长、周期和振幅。因此水平方向的运动速度Vh变为
(8)
us的引入并不会很灵敏地影响海表面的斜率分布。在这些基础上我们可以计算由于海表面波面运动引起的激光径向方向的多普勒信息:
VLOS=-Vhsinθ+Vycosθ
(9)
θ是激光的入射天底角,负号表示正向的水平速度引起激光束径向上负的多普勒频移(图1所示)。
在第一步的仿真计算中,暂不考虑us的影响,us只引起激光多普勒信息的整体偏移。海表面波形的成因是复杂的,为了更真实地模拟海表面波形,需要将多个波长L和振幅A的海面波进行叠加,体现为高振幅波对小振幅波的简单调制,让波形更接近真实波。图4为模拟的不同情况下海表面波形的斜率分布直方图,采用多波幅的模型叠加,相比单波幅,更好地体现了高斯线型的海表面斜率分布特征。

图4 海表面斜率分布直方图Fig.4 Histogram of sea surface slope with differet wave superpositions
图5为2个主波周期内海表面波形及代表点的速度矢量仿真模拟,采用3个波长L和波幅A的叠加(L1=5m,A1=0.3 m;L2=1 m,A2=0.05 m,L3=0.05 m,A3=0.003 m)。曲线表示波形,箭头表示波面的运动速度矢量,波面所有点的水平速度在0~1.05 m/s内变化,垂直速度在0~1.21 m/s范围内变化。
将海表面速度矢量投影到激光径向方向,便可以计算激光海面散射信号的多普勒信息。图6为计算的在2周期内激光海面作用点的径向速度分量(激光入射天底角为20°),速度分量在-1.2m/s~1.3m/s,该速度会叠加在多普勒激光雷达的径向速度之上。空间激光雷达光束具有空间尺寸,假设飞机飞行高度为8 km,激光发散角为100 urad,单脉冲海面探测光斑大约0.8 m,进而可以计算这个空间范围内多普勒激光雷达海表信号径向速度的平均值,速度值在-1.08 m/s~1.02 m/s范围内变化。当然,空间多普勒激光雷达普遍采用多脉冲的时间积分探测,这时海表面的速度分量将体现为时间平均效果,2周期内的速度平均值为-0.04 m/s。当然,平均值的大小与激光入射天底角有关,如果增大激光入射天底角到40°,激光海面作用点的径向速度分量都会相应增大,但2周期内的平均值仍较小(<0.2 m/s)。
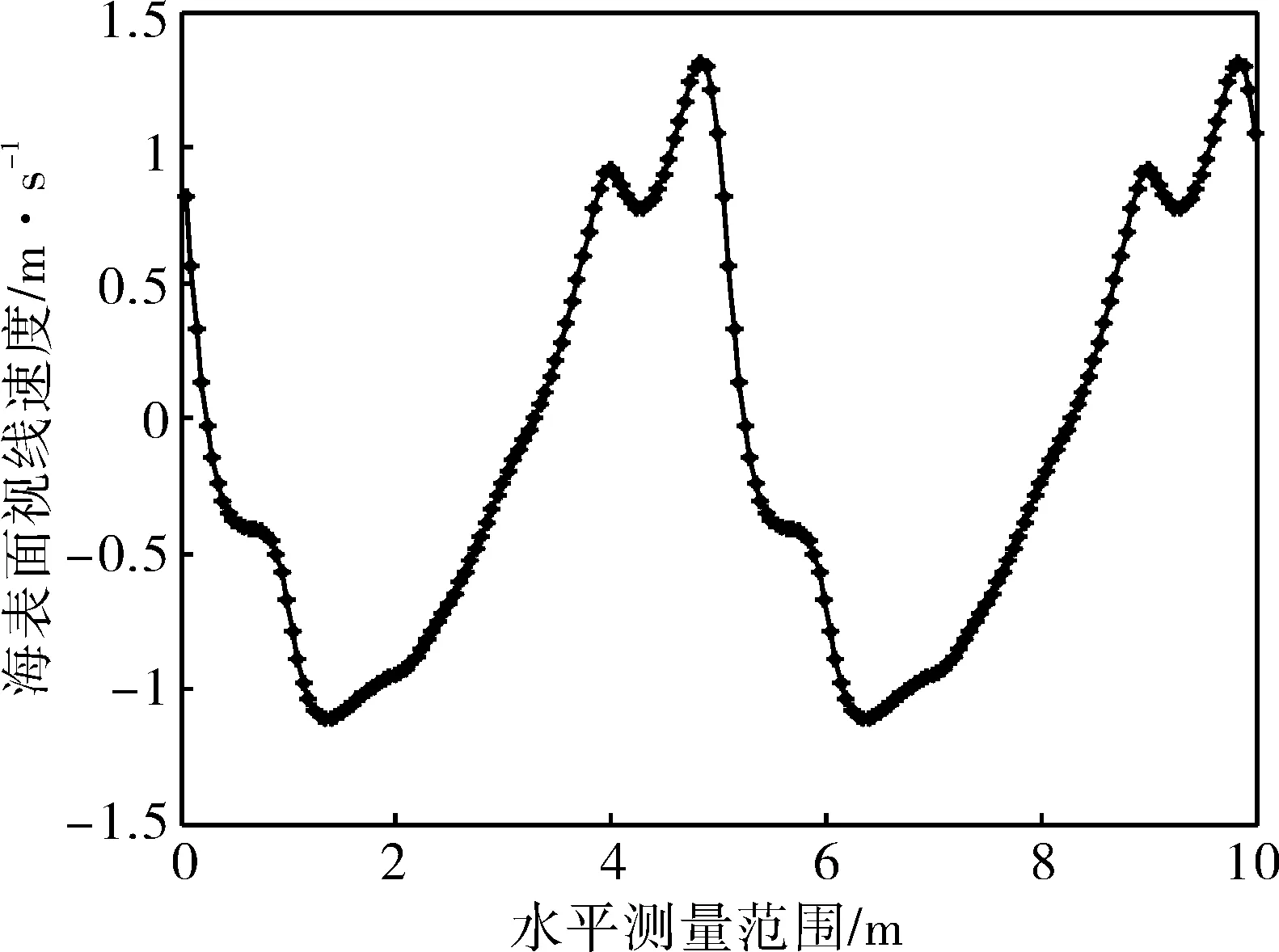
图6 波面运动引起的激光海表面散射作用点的径向速度(2个波周期范围,光束直径约0.8 m)Fig.6 Radial velocity at scattering action point on laser sea surface caused by wave movement(with footprint diameter of 0.8 m and in two periods)
可见,如果采用时间积分测量,海表散射信号的多普勒平均效果好,海表运动的影响小,对于激光雷达的速度校准具有应用价值,但如果再考虑强海表面风推动海面波的整体漂流速度us(引起的速度分量最大为ussinθ),该速度在某些时候并不能被完全的忽略掉。考虑这些因素影响,如果激光雷达系统采用锥形扫描探测机制,实现多方向扫描探测,那么海表面散射信号的多普勒将会实现时间和空间的测量平均,海面的多普勒影响可以在时空平均过程中相互消除掉,这时海表面散射可以用来校准系统的零风速。
4 结论
本文从激光海表面散射信号的强度和速度特征方面进行了仿真和实验分析,结果表明:
1) 对于355 nm出射激光,考虑了海水体散射贡献后,海表面反射率模型曲线与实验数据的处理结果吻合较好,海表面风速的理论值和实际值接近,验证了受海表面风驱动的海表面反射率特征。
2) 多普勒激光雷达如果采用定向探测,海表面的运动会一定程度上产生激光海面信号的多普勒特征,只考虑波面的水平和垂直运动,速度平均值<0.2 m/s,对于激光雷达的速度校准具有应用价值。如果采用锥形扫描探测机制,海表面散射信号可以更好地用来实现多普勒激光雷达系统的零风速校准。
[1] Durand Y, Chinal E, Endemann M, et al. ALADIN airborne demonstrator: a Doppler wind lidar to prepare ESA’s aeolus explorer mission[J]. SPIE,2006,6296: 13-17.
[2] ESA European Space Agency.ADM-Aeolus science report[R]. German:ESA European Space Agency,2008.
[3] Reitebuch O, Endemann M,Engelbert D, et al. Pre-launch validation of ADM-Aeolus with an airborne direct-detection wind lidar[J]. USA:Boulder Colorado, 2008, 41-44.
[4] Weissmann M, Busen R,Dörnbrack A, et al. Targeted observations with an airborne wind lidar[J]. J. Atmos. Oceanic Technol., 2005, 22(11): 1706-1719.
[5] Cutten D R, Rothermel J, Jarzembski M A, et al. Radiometric calibration of an airborne CO2pulsed Doppler lidar with a natural Earth surface[J]. Applied Optics, 2002,41(18): 3530-3537.
[6] Albert A. An analytical model for subsurface irradiance and remote sensing reflectance in deep and shallow case-2waters[J]. Optics Express, 2003,11(22):2873-2890.
[7] Hu Y,Stamnes K,Vaughan M, et al. Sea surface wind speed estimation from space-based lidarMeasurements[J]. Atmos. Chem. Phys., 2008, 8(13):3593-3601.
[8] Wu Dong, Zhang Xiaoxue, Yan Fengqi. Sea surface wind speed detection by using the data of CALIPSO lidar[J]. Acta Optica Sinica, 2013,32(8):243-249. 吴东,张小雪,阎逢旗.基于星载激光雷达数据的海面风速探测[J]. 光学学报, 2012, 32(8):243-249.
[9] Josset D, Zhai Pengwang, Hu Yongxiang, et al. Lidar equation for ocean surface and subsurface[J]. Optics Express, 2010, 18(20):20862-20875.
[10]Li Zhigang,Lemmerz C, Paffrath U, et al. Airborne doppler lidar investigation of sea surface reflectance at an 355 nm ultraviolet wavelength[J].J. Atmos. Oceanic Technol., 2010, 27(4):693-704.
[11]Fournier A, Reeves W T. A simple model of ocean waves[J]. Computer Graphics, 1986, 20(4): 65-74.
Analysis on sea surface scattering of Doppler lidar in space
Li Zhigang,Tian Maobin, Zhu Linwei
(School of Physics and Optoelectronic Engineering, Ludong University, Yantai 264000,China)
In order to validate the sea surface reflectance model stressed by wind and calculate the accuracy of zero-wind calibration by sea surface return, the intensity and velocity characters of sea surface return were analyzed. For the intensity characters, we compared the sea surface reflectance model to the Doppler lidar observation data, with the consideration of the contribution from subsurface reflectance, and a good consistent was showed with the local sea surface windspeed in the result referring to the windspeed of QuikSCAT sea surface. For the velocity characters, we simulated the sea wave shape with considering the vertical and horizontal movement and calculated the sea surface velocity information.The zero-wind correction accuracy for Doppler lidar with the temporal integral measurement was less than 0.2 m/s.
Dopper lidar; sea surface backscattering; zero-wind calibration;wave motion
1002-2082(2015)06-0959-06
2015-07-27;
2015-09-10
国家自然科学基金(41206003),山东省自然科学基金(ZR2012DQ010)
李志刚(1980-),男,山东莱芜人,博士,主要从事大气激光雷达探测方面的研究。E-mail:lizg_ldu@126.com
TN249; O439
A
10.5768/JAO201536.0605002
