布拉格光栅应变测试系统的动态标定

王 康,顾金良,罗红娥

(南京理工大学 瞬态物理国家重点实验室，江苏 南京 210094)



布拉格光栅应变测试系统的动态标定

王 康,顾金良,罗红娥

(南京理工大学 瞬态物理国家重点实验室，江苏 南京 210094)

为了能够简单精确地标定出Bragg光栅应变测试系统的应变拉伸系数，通过分析测试系统的解调原理，提出了运用陶瓷制动器的逆压电效应标定该系统的方法。对系统的8路应变测试通道进行了标定实验，将每路通道的实验数据进行线性拟合，分别得到了Bragg光栅应变拉伸量与解调信号相位差的关系曲线，从而确定了每路通道的应变拉伸系数，分析表明系数的标定相对误差在±0.002 μm/(°)以内，标定结果具有较高的精度。

Bragg光栅；应变测试；动态标定；陶瓷制动器

引言

在一些强电磁干扰的特殊环境下，运用应变电桥原理的传统应变电测法，会存在电源供电不稳定，应变片检测的应变信号被电磁场干扰信号所淹没等问题，无法进行正常的动态应变测试。利用光纤光栅构建的动态应变测试系统，可以很好地解决上述传统应变电测法所存在的问题[1-2]，因其具有抗电磁干扰能力强、灵敏度高、结构简单、易于复用等优点，成为了最近20年来国内外的研究热点[3-7]。

为了实现应变量的准确测量，测试前必须进行标定实验，国内外学者对此也做了一些标定实验。2008年，郑卜祥等人利用等强度梁对Bragg光栅进行了应变量的标定实验[8]。2013年，黄旌等人通过所设计的等强度加载平台进行了应变量大于5 000 的标定实验[9]。目前绝大多数的应变标定实验都是将Bragg光栅粘贴在等强度悬臂梁上，同时粘贴一组电阻应变片构成应变电桥，通过应变片测得的应变量与Bragg光栅应变测试系统所采集到的数据进行对比，实现应变量的标定。该方法中等强度悬臂梁的厚度、绕度、Bragg光栅与应变片的固定位置等都会使得标定结果产生较大误差，并且该方法不能够标定出Bragg光栅应变拉伸量与解调信号之间的关系，从而在后续的应变测试中无法测得实际的应变拉伸量。为了解决上述问题，本文提出了一种运用陶瓷制动器的逆压电效应对Bragg光栅应变测试系统进行动态标定的实验方法，在结合了系统解调原理的基础上设计了标定实验方案，并对系统的8路应变测试通道进行了标定实验，标定结果具有较高的精确度。

1 三步移相解调法

测试系统的解调部分采用非平衡M-Z干涉仪结构，由2×2耦合器和3×3耦合器构成，最终带有应变成分的干涉光从3×3耦合器等分成3条支路输出，由于3×3耦合器输出端的光强是平均分配的，即每个端口的输出光强相等，所以3路光信号的直流分量和交流分量的最大值相等。除此之外，3路信号彼此之间的相位差为120°，所以3×3耦合器3个输出端光强分别为

(1)

式中：Id为光强的直流分量；Ia为光强的交流分量。

对(1)式进行变形运算，消除其中的直流分量和交流分量，得出干涉场的相位为

(2)

在实际解调过程中，只需将所得的相位值分别减去应变量为零时的相位值，即可得到相对的相位差，另外由于制作工艺的问题，使得3×3耦合器的3个输出端不对称，它们之间的相位差有时并不是精确的120°，文献[10]提供了3个输出端之间相位差具体的计算方法，但是通常来说，3个输出端的相位差误差范围在±10°以内[11]，对于动态应变信号的解调影响不大，是可以接受的。

由于反三角函数的多值性，解调后的相位总是在±90°范围内周期性变化，要想解算出与实际应变成线性关系的相位，需要进行算法处理，具体的方法为假设解算出的相位值为φ，当测试点的应变量增加时，φ从±90°的范围内连续增加，并在达到+90°临界值时返回到-90°处，以此继续在±90°的范围内连续增加，因此当数据之差大于100时，从突变数据开始其后面的数据依次加π，依此类推，从而解算出应变增加时与之相关的实际相位值。当应变减少时，正好与应变增加的情况相反，仿照应变增加的方法，解算出应变减少时实际的相位值。

2 标定方案

系统标定结构框图如图1所示，对于非平衡M-Z干涉仪，干涉系统的两臂相位差为

(3)

图1 系统标定结构框图Fig.1 Structure block diagram of system calibration

对(3)式中的波长进行微分并根据Bragg光栅传感原理，可以将表达式改写成为

(4)

在驱动电源的作用下陶瓷制动器会因为自身的逆压电效应产生纵向拉伸，而陶瓷制动器的纵向拉伸量与应变量存在线性关系，由于Bragg光栅粘贴在陶瓷制动器上，所以Bragg光栅的纵向拉伸量与陶瓷制动器的纵向拉伸量保持一致，这样可以得到：

(5)

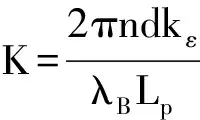
Δφ(λB)=k·ΔL

(6)

Bragg光栅粘贴在陶瓷制动器上，在驱动电源的作用下，Bragg光栅与陶瓷制动器的纵向拉伸量保持一致。由(6)式可知相位的变化量与Bragg光栅感受到的纵向拉伸量成线性关系，而线性系数K为Bragg光栅应变测试系统的应变拉伸系数，这是最终需要标定的系数。Bragg光栅中带有纵向拉伸应变信息的反射光从2×2耦合器的另一个端口输出进入由2×2和3×3耦合器组成的非平衡M-Z干涉仪中，从耦合器3个端口输出的干涉光信号被PIN管转换为电信号，经过后续的信号调理电路后进入数据采集卡，最终所采集的信号在上位机上显示，通过编写三步移相解调算法，消除3路信号的直流分量和交流分量，还原出最终的相位信号。而陶瓷制动器的纵向拉伸量与驱动电源电压的对应关系由厂家提供标定。

通过以上分析可以把标定方案的具体步骤归结为：

1) 按照图1中系统标定结构框图搭建好标定实验平台。

2) 使用驱动电源给陶瓷制动器输入一个固定电压值的阶跃信号并查找厂家提供的标定数据得到该电压值下陶瓷制动器的纵向拉伸量。

3) 通过编写的三步移相解调算法将采集到的3路信号还原为相位变化量。

4) 通过(6)式的计算即可得到系统的应变拉伸系数K。

3 实验与数据分析

本次标定实验使用的是5mm×5mm×10mm的OEM型陶瓷制动器，配套的驱动电源型号为HPV-1C0150A0500。驱动电源具有手动调节和自动输出电压波形功能，输出电压范围为0～150V、稳定性为0.1%FS/8h、电源纹波最大值为10mV。陶瓷制动器在不同电压的驱动下会产生不同的纵向拉伸量，本次标定实验采用的阶跃信号是从电压为0时开始上升到某一个具体电压，而电压与陶瓷制动器位移的具体关系由生产厂家在恒温恒压恒湿的条件下标定。

图2 标定系统实物图Fig.2 Physical map of calibration system

标定系统实物图如图2所示。系统由8路非平衡M-Z干涉仪组成，由于干涉仪中耦合器本身制作工艺的差别，导致了每条干涉光路的光程差不同，所以系统每路通道的纵向应变拉伸系数是不相同的，这里以第一个干涉通道为例进行说明。

使用驱动电源给陶瓷制动器输入一个120 V的阶跃信号，陶瓷制动器由于逆压电效应产生纵向拉伸应变，粘贴在其表面上的Bragg光栅的中心波长发生偏移，带有拉伸应变信息的光信号通过非平衡M-Z干涉仪之后从3×3耦合器的输出端输出3路干涉信号，干涉信号经过光电转换、放大、滤波之后被数据采集卡采集，采集到的电压信号如图3所示。

图3 120 V阶跃信号输出电压曲线Fig.3 Output voltage curve of 120 V step signal

采集到的信号还需进行三步移相解调算法处理，在通过三步移相、数字滤波、相位提取等算法之后可以得到该阶跃信号下解调的相位值为181.61°，经过(6)式的计算可以得到该通道的纵向应变拉伸系数。为了使得标定误差降到最低，设定驱动电源输出阶跃信号的起始值为10 V,终止值为140 V,中间步长间隔为5 V/步，分别记录下每个电压下干涉通道采集到的数据经过解调之后的相位值，标定数据如表1所示。

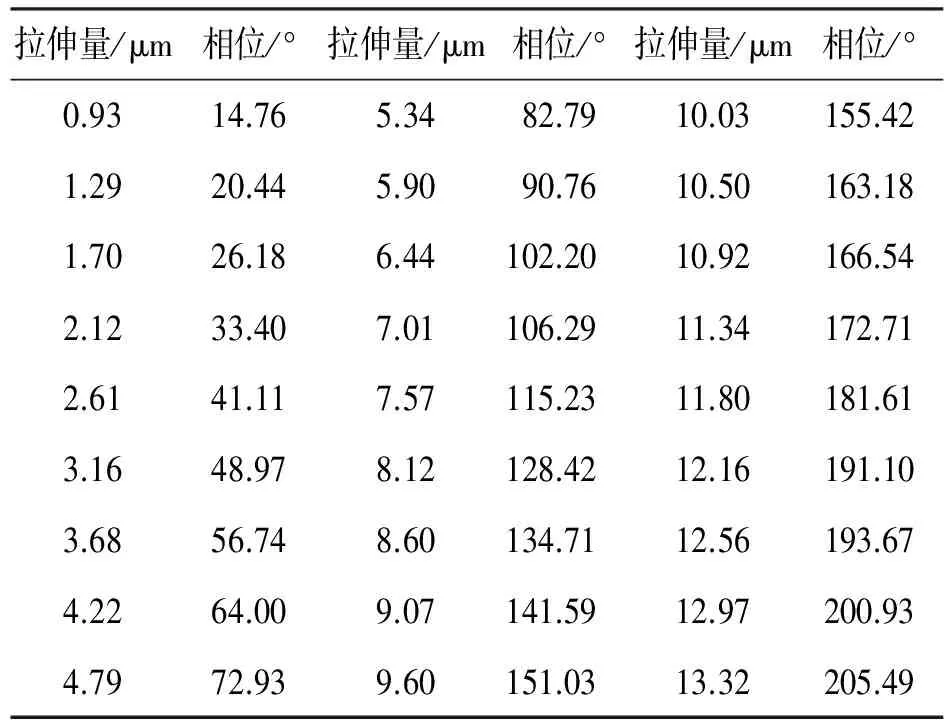
表1 通道1标定数据

其余通道的标定方法与通道1类似，最终利用Matlab软件进行最小二乘拟合得到每路干涉通道的相位与Bragg光栅拉伸量的线性曲线，如图4、图5所示。每条拟合曲线的斜率即为每路干涉通道的应变拉伸系数，分别为

K1=0.065 1 μm/°，K2=0.037 9 μm/(°)，

K3=0.045 8 μm/°，K4=0.054 5 μm/(°)，

K5=0.060 2 μm/°，K6=0.051 7 μm/(°)，

K7=0.090 3 μm/°，K8=0.061 8 μm/(°)。

通过分析实验数据，利用(6)式计算出每路通道的每组数据的应变拉伸系数，将每路通道标定出的应变拉伸系数的最大值与最小值相减可以得到每路通道的系数标定相对误差范围(设相对误差系数为X)为

X1=±0.002 0 μm/°，X2=±0.001 5 μm/(°)，

X3=±0.001 8 μm/°，X4=±0.001 9 μm/(°)，

X5=±0.001 2 μm/°，X6=±0.000 8 μm/(°)，

X7=±0.001 8 μm/°，X8=±0.001 4 μm/(°)。

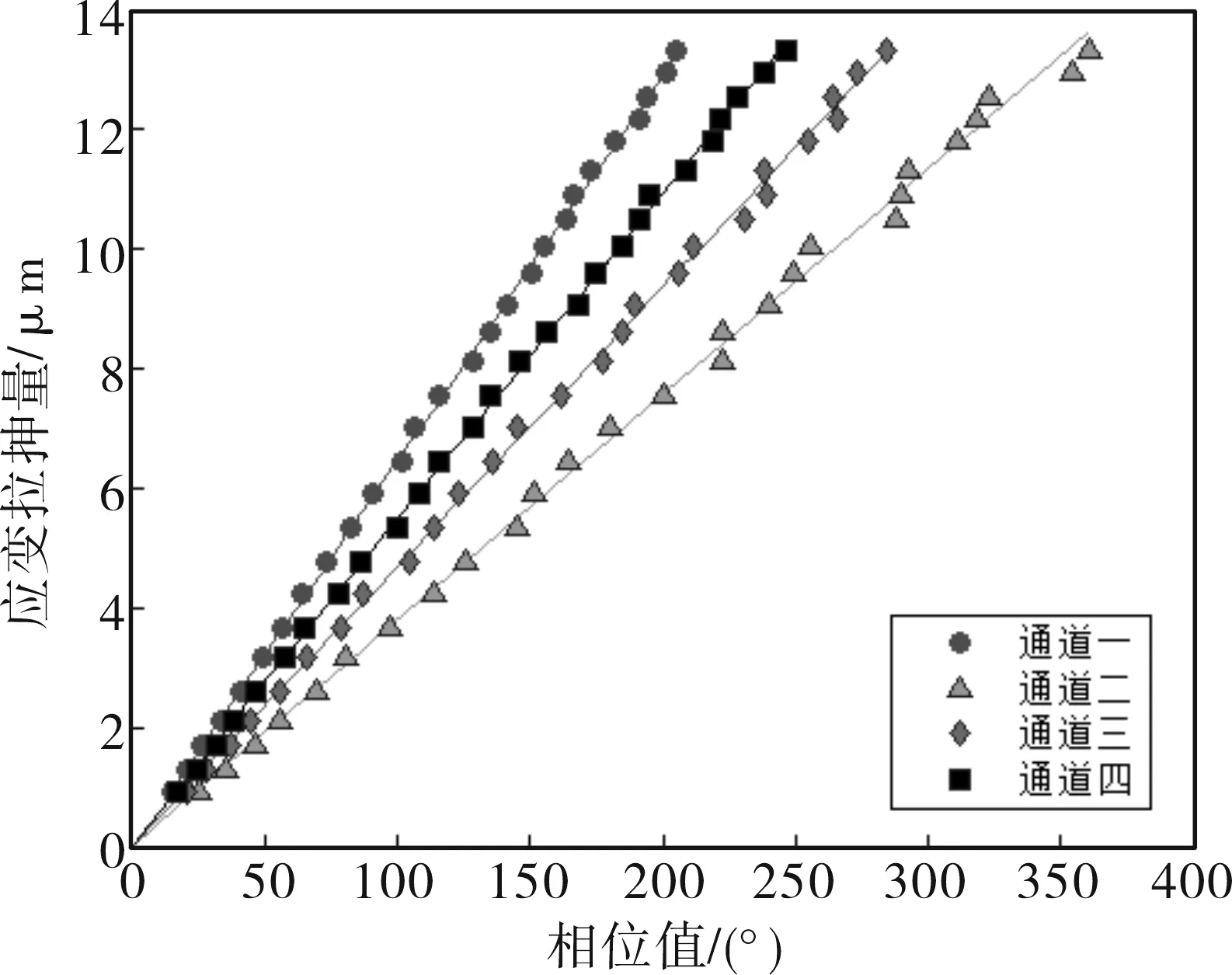
图4 通道1-4应变标定曲线图Fig.4 Channel 1-4 stain calibration curve

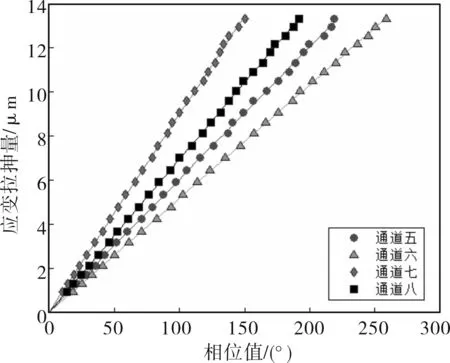
图5 通道5-8应变标定曲线图Fig.5 Channel 5-8 stain calibration curve

4 结论

在利用Bragg光栅应变测试系统进行动态应变测试实验之前，必须对测试系统进行系数标定。本文介绍了一种利用陶瓷制动器的逆压电效应进行系统应变拉伸系数标定的方法。通过每路通道的实验数据线性拟合的结果可以看出该方法对于Bragg光栅应变测试系统的标定具有较高的精度，标定系数最大误差范围仅为±0.002 μm/(°)，为后续准确测得物体的动态应变拉伸提供了帮助。

[1] Zhang Weigang, Liang Longbin, Zhao Qida，et al. Contrast analyses of strain measurement of fiber grating and resistance strain chip[J]. Journal of Sensors and Actuators, 2001, 3: 200-205. 张伟刚，梁龙彬，赵启大,等.光纤光栅与电阻应变测量的对比分析[J].传感技术学报，2001，3: 200-205.

[2] Shen Haowen, Zhu Pingyu, Shi Wei, et al. Experimental study on strain measurement under magnetic field of fiber bragg grating and resistance strain gauge[J]. Automation and Information Engineering, 2014, 35(4):11-15. 申昊文，朱萍玉，施为,等.光纤光栅与电阻应变片磁场环境下应变测量的试验研究[J].自动化与信息工程，2014,35(4):11-15.

[3] Li Li, Lin Yuchi, Shen Xiaoyan,et al. Fiber bragg grating sensor system for dynamic strain measurement[J]. Journal of Sensors and Actuators, 2007, 20(5):994-997. 李丽，林玉池，沈小燕,等.Bragg光栅在动态应变测量中的研究[J].传感技术学报，2007，20(5): 994-997.

[4] Chen Xiaomei. The prospect of applying FBG sensor in micrometrology[J]. Airborne Measurement Technology, 2004, 24(2):1-3. 陈晓梅.FBG 传感器微为尺度计量中应用的前景[J]. 航空计测技术，2004，24(2): 1-3.

[5] Hao WenLiang, Zhen Shenglai, Cao Shenggang,et al. A fiber bragg grating interrogating dynamic strains sensor system based on interference of polarized mode[J]. Journal of Quantum Electronic, 2012,29(4):507-512. 郝文良，甄胜来，曹胜刚,等.基于偏振模干涉的光纤光栅动态应变解调系统[J].量子电子学报，2012, 29(4): 507-512.

[6] Zhu Pingyu, Lin Yuchi,Wang Wei. Fiber bragg grating sensor for high frequency strain measurement[J]. Optoelectronic Engineering, 2007, 34(6):135-139. 朱萍玉，林玉池，王为.Bragg光栅用于高频应变测试的研究[J].光电工程，2007，34(6):135-139.

[7] Li Zhizhong, Zhou Weilin, Yang Huayong. High frequency vibration measurementwith fiber grating sensing based on unmatched interferometer[J]. Optical Communication Research, 2004, 5: 55-57. 李智忠，周伟林，杨华勇.非平衡干涉检测光纤光栅高频振动传感研究[J].光通信研究，2004，5: 55-57.

[8] Zheng Buxiang, Song Yonglun, Zhang Dongsheng, et al. Experimental study on temperature and strain sensing characteristics of fiber bragg grating[J]. Instrument Technique and Sensor, 2008, 11:12-15. 郑卜祥，宋永伦，张东生,等. Bragg光栅温度和应变传感特性的试验研究[J].仪表技术与传感器，2008, 11:12-15.

[9] Huang Jing,Liu Chengwu, Wei Dong,et al. Discussion on large strain calibration method using FBG sensor[J]. Equipment environment engineering, 2013,10(4):86-89. 黄旌，刘成武，魏东,等.光纤FBG传感器实施大应变标定方法的探讨[J].装备环境工程，2013,10(4):86-89.

[10]Li Dong, Wang Zhihuai, Zeng Wenfeng, et al. Research on deliering characteristic of unbalanced fiber Mach-Zehnder interometer based 3 ×3 coupler[J]. Laser and Infrared, 2010, 40(8):884-886. 李东，王志怀，曾文锋,等.基于3 ×3耦合器的非平衡光纤Mach-Zehnder干涉仪传输特性研究[J].激光与红外，2010，40(8): 884-886.

[11]Jang Yi, Lou Yingming, Wang Huiwen. Software demodulation for 3 ×3 coupler based fiber optical interferometer[J]. Acta Photonic Sinica, 1998, 27(2):152-155. 江毅，娄英明，王惠文. 基于对称3×3耦合器的光纤干涉信号的软件解调技术[J].光子学报, 1998, 27(2): 152-155.

Dynamic calibration for Bragg grating strain measurement system

Wang Kang， Gu Jinliang， Luo Honge

(National Key Laboratory of Transient Physics, NUST, Jiangsu 210094, China)

In order to calibrate the strain stretch coefficient of Bragg grating strain measurement system simply and precisely, on the basis of the analysis of the demodulation principle of the measurement system, we proposed the method for using inverse piezoelectric effect of lead zirconate titanate (PZT) to calibrate the system and carried out the calibration experiment on the 8 strain measurement channels. The relationship curves of the strain and the phase difference between demodulation signals were obtained by the linear fitting of the experimental data of each channel,and the strain sensing coefficient of each channel was determined by the relationship curves. Analysis shows that the coefficients of the calibration relative error is within ±0.002 μm/(°), the results have higher accuracy.

Bragg grating; strain measurement; dynamic calibration; PZT

1002-2082(2015)06-0913-05

2015-07-17；

2015-08-26

王康(1991-)，男，江苏南京人，硕士研究生，主要从事测试计量技术及仪器研究。

E-mail：jtrharry@qq.com

TN253；TP216

A

10.5768/JAO201536.0603003