基于内部级数法的高均匀度磁传感器标定装置设计

金 多，程德福，王言章，周志坚

(吉林大学仪器科学与电气工程学院，吉林长春 130061)



基于内部级数法的高均匀度磁传感器标定装置设计

金 多，程德福，王言章，周志坚

(吉林大学仪器科学与电气工程学院，吉林长春 130061)

在对磁传感器进行标定时，Maxwell线圈在磁梯度场均匀度要求高且对线圈空间尺寸有严格限制时并不适用，针对这个问题设计了一种具有高均匀度的磁梯度线圈作为磁传感器标定装置。应用内部级数法对单个轴对称线圈产生的磁场进行数理分析，进而得到其磁场梯度分布的一般特性，在此基础上计算出高均匀度磁梯度线圈的结构参数与均匀度。对线圈模型进行仿真分析并完成了磁梯度线圈装置的设计和制作。最后，根据仿真结果与实际测量得到的数据，验证了设计的正确性。

磁传感器；内部级数法；均匀度；标定；仿真

0 引言

在磁法勘探领域，与传统的磁场测量相比，磁梯度测量有着显著的优势，如对磁分辨率高，基本不受地磁日变和正常场等因素的影响等[1-2]，磁梯度测量已在航空磁测、海洋磁测及井中磁测等领域得到广泛的应用[3-4]。而在磁传感器研制过程中，可通过标定的方法来检测其磁梯度测量的性能指标，一般选择磁梯度线圈作为标定装置。

在现有的磁梯度线圈装置中，最常见的是Maxwell线圈，它和Helmholtz线圈的设计方法类似，区别仅仅是电流的方向和线圈半径与间距的关系[5]，Helmholtz线圈可以产生一定均匀度的均匀磁场，而Maxwell线圈则可以产生均匀磁梯度场。但是Maxwell线圈所产生的磁梯度场的均匀度不高，在对均匀度要求高的场合下，只能通过增大线圈的几何尺寸来满足要求。显然，这样不仅在制作线圈与实际应用时非常不便，而且在对线圈空间尺寸有严格限制时，Maxwell线圈已经不能满足设计要求。针对这个问题，提出了一种高均匀度磁梯度线圈的设计方法，该方法采用内部级数法[6]，即将线圈的磁场梯度展开成级数形式，计算出线圈的几何尺寸和电流大小使级数的系数变为零，从而显著提高均匀磁梯度场的均匀度。

1 单个轴对称线圈的磁场梯度分析

无论磁场线圈的结构如何变化，其基本单元都是单个轴对称圆环线圈，所以首先应分析单个圆环线圈的磁场梯度分布情况，以此为基础来设计高均匀度磁梯度线圈装置。

根据电磁场理论可知，在没有电流存在的区域，必定存在标量磁位Um，并且其满足拉普拉斯方程

▽Um=0

(1)

通过解拉普拉斯方程，可以得到线圈在中心点附近的磁场强度的级数形式[7]：

(2)

(3)

式中：r和θ为球坐标分量;Hz和Hρ分别为磁场强度的轴向分量和径向分量;Pn为n阶勒让德多项式。

由上式可知轴对称线圈产生的磁场有轴向分量磁场Hz(r,θ)与径向分量磁场Hρ(r,θ)，并且在原点附近轴向分量磁场远大于径向分量磁场。根据勒让德多项式的性质︱Pn(cosθ)︱≤1，可知轴向分量磁场又以线圈轴线上的轴向分量磁场变化最快，所以在分析磁场梯度的均匀度时，只需分析其轴线上的磁场梯度变化。

在线圈的轴线上，即θ=0，r=Z处，线圈的轴向分量磁场强度为

(4)

可以看出式(4)实际上就是线圈在它轴线上的磁场强度H(0，0，Z)在中心点附近的泰勒展开式。而泰勒系数的表达式

(5)

对于单个轴对称圆环线圈，可以得到系数An的表达式[8]：

(6)

式中：R为圆环线圈的半径；I为线圈电流；β为线圈圆心在轴线上的坐标与线圈半径之比；Ln(β) 为圆环线圈的磁场系数。

同时可以得到单个轴对称圆环线圈轴线上磁场梯度的表达式：

(7)

磁场梯度的均匀度定义为一定半径球面上的磁场梯度相对于圆心点的磁场梯度的相对变化量，这个变化量越小，磁梯度线圈所具有的均匀度越高。均匀度表达式为

(8)

式中r为球形均匀区域的半径。

2 高均匀度磁梯度线圈设计

通过对单个轴对称线圈的磁场梯度分析，将磁场梯度用级数的形式表达，由式(7)可知，磁场系数L1(β)决定了线圈在它中心点的磁场梯度大小，而其余磁场系数Ln(β)(n=2,3,4,…)则决定了线圈在中心附近各点的磁场梯度相对于中心点磁场梯度的偏离程度。所以为了得到更高的均匀度，在设计线圈装置时应尽可能使磁场系数L2(β)=L3(β)=L4(β)=…=Ln(β)=0，可通过两对圆环线圈按一定参数关系组合的方式来实现。

图1为高均匀度磁梯度线圈结构图，该系统由两对关于xOy平面对称的圆环线圈组成，线圈半径分别为R1、R2，线圈中的电流分别为I1、I2，电流方向相反，线圈圆心位于z轴上，并且线圈圆心与坐标原点的距离分别为a1、a2。由圆环线圈的磁场系数特性可知，其奇次项系数是关于β的奇函数，由于两对圆环线圈关于xOy平面对称且电流方向相反，所以线圈系统中将不存在偶次项，对于整个线圈系统，其磁场梯度表达式为

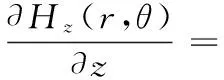
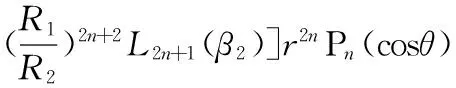
(9)

式中：β1=a1/R1;β2=a2/R2。

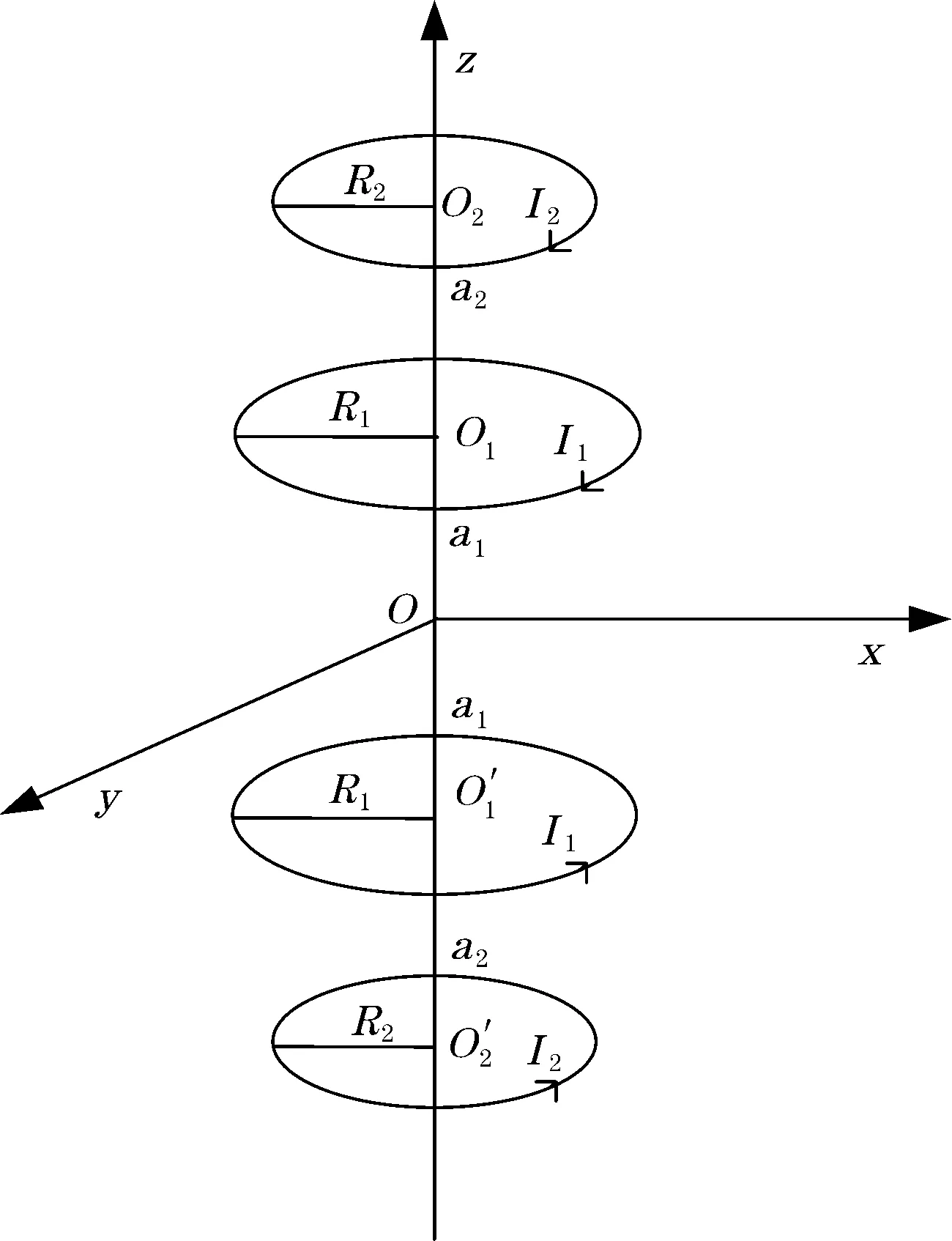
图1 高均匀度磁梯度线圈结构图

为使线圈系统具有高均匀度的磁场梯度，应选择合适的线圈结构参数，即磁场系数表达式中的4个未知数I1/I2、R1/R2、β1与β2，使其磁场系数为零。设I1=I2，在此条件下求解磁场系数的方程组可以得到线圈系统的其余3个结构参数关系：

(10)

式(10)为非线性方程组，无法获得解析解，应用Matlab里的fsolve函数可求得方程组的数值解。它的求解方式为：[x,fval]= fsolve(fun,x0,options)。其中，fun是用于定义需求解的非线性方程组的函数文件名，x0是变量初值，options用于对优化参数的设置。通过求解可以得到：β1=0．539 3，β2=1．513 1，R1/R2=1．635 5。同理，可以分别在R1=R2，a1=a2即β1/β2=R2/R1的条件下分别计算出高均匀度磁梯度线圈的结构参数关系，同时根据式(8)可以得到在不同结构参数关系下线圈系统的均匀度，如表1所示。通过以上分析可知，如果继续增加圆环线圈，线圈系统理论上将具有更高的均匀度。但是由于内部级数法本身的局限性，实际上均匀度并不能达到理论计算值。

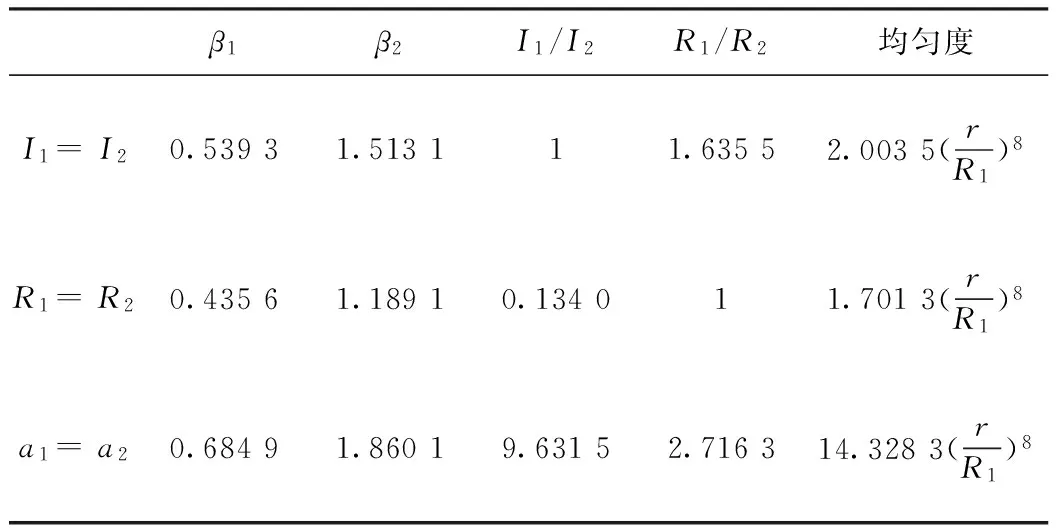
表1 不同条件下高均匀度磁梯度线圈的结构参数与均匀度

3 实验验证

项目要求磁传感器标定装置可以在边长为15cm的正方体空间范围内产生100pT/m的磁场梯度，精度为0．1%，同时要求装置占用的空间在边长为70cm的正方体范围内。根据设计要求与均匀度的定义可计算出均匀磁梯度场应在r=11 cm的球形空间范围内，如果采用Maxwell线圈作为标定装置，根据其均匀磁场梯度表达式[9]

(11)

与均匀度表达式

(12)

可以计算出Maxwell线圈的直径应为90．8 cm。显然，已经超过设计要求的空间范围，不能满足设计要求。由表1可知，在R1=R2的线圈结构参数关系下，线圈的均匀度最高，并且相对于a1=a2与I1=I2这两种线圈结构，加工制作简单，结构稳定，应用方便。如采用这种结构的线圈作标定装置，根据设计的要求可以计算出线圈参数：R1=R2=28 cm；I1=1．65 μA；I2=12．29 μA；a1=12．2 cm；a2=33．3 cm。可见，线圈的结构参数符合磁传感器标定装置的尺寸要求。

3．1 模型仿真

根据以上分析所得到的线圈参数，可对线圈参数模型仿真。仿真实验采用COMSOL Multiphysics仿真软件[10]。仿真过程主要包括全局定义、模型设置、求解与后处理。在全局定义中设置线圈中的电流参数。在模型设置中根据线圈的结构参数按照1∶1的比例绘制三维线圈模型，同时构建模型的求解区域。模型建立之后进行网格划分，根据计算机性能合理地设置网格大小，一般网格划分越小、密度越大时，仿真结果具有更高的准确性。以上过程完成之后可以对模型进行求解。

为分析线圈模型所产生的均匀磁梯度场，在仿真得到线圈的磁场分布情况后，在线圈轴线上以坐标原点为起点，沿z轴正方向取11 cm长的直线，分析这条直线上的磁场梯度变化情况，如图2所示。在理论计算时线圈中的电流为线电流，而仿真过程中由于线圈绕组截面的影响，仿真所得磁场梯度值小于理论值。并且由于内部级数法的局限性，距离线圈中心越远，与理论值误差越大，但整体误差在0．1%的精度要求范围内，这证明设计方法正确。

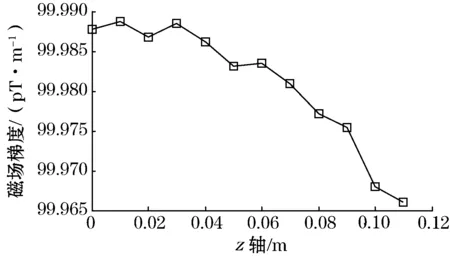
图2 线圈轴线上磁场梯度仿真值

3．2 试验测量

为防止外部环境磁场的干扰，整个测量过程在屏蔽室中进行，屏蔽室的屏蔽度为60 dB．线圈装置的供电电源为恒流源，选用6221型直流电流源，其电流精度为0．05%。选用Mag-03MS型三轴磁通门传感器测量磁场，其测量范围为-70～70 μT，线性误差小于0．001 5%．综合考虑线圈装置的加工精度与安装误差，其总体测量不确定度小于0．1%．测量时传感器从线圈装置的中心位置开始，为保证传感器沿轴线以确定距离移动，采用了专用机构，并且每隔1 cm进行1次磁场测量。对测量结果处理得到轴线上各点的磁场梯度值，如图3所示。试验测量的梯度值与理论值误差在0．1%范围内，而且测量值与仿真值的变化趋势相同，距离线圈中心越远，磁场梯度越小。同时，由于实际测量环境与线圈装置制作精度的影响，测量值要小于仿真值。

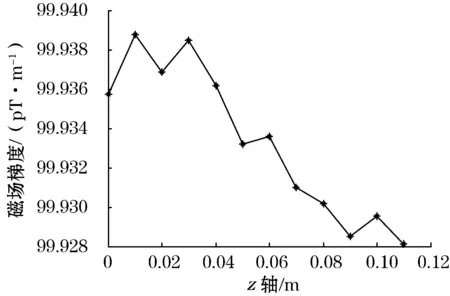
图3 线圈轴线上磁场梯度测量值

4 结束语

本文应用内部级数法设计了具有高均匀度的磁梯度线圈装置，完成了线圈模型的仿真并进行了实际测量，结果表明：线圈装置可以在边长为15 cm的正方体空间范围内产生100 pT/m的磁场梯度，精度优于0．1%，可应用于磁传感器的标定。同时，根据本文的内部级数分析方法，在以后设计不同指标的高均匀度磁传感器标定装置时可方便、快捷地确定线圈的各项参数。

[1] 杨威,王传雷．规则形体垂直磁梯度场研究及应用．工程地球物理学报,2012,9(3):326-331．

[2] 张昌达．航空磁力梯度张量测量——航空磁测技术的最新进展．工程地球物理学报,2006,3(5):354-361．

[3] NABIGHIAN M N,GRAUCH V J S,HANSEN R O,et al．The historical development of the magnetic method in exploration．Geophysics,2005,70(6):33 -61．

[4] 吴嘉慧,施文康．磁通门技术在检测中的应用．仪表技术与传感器,2000(12):33-34．

[5] 陈竹年．磁场梯度线线圈的设计．电测与仪表,1994(1):18-19．

[6] GARRETT M W．Thick Cylindrical Coil Systems for Strong Magnetic Fields with Field or Gradient Homogeneities of the 6th to 20th Order．J．Appl．Phys．,1967,38(6):2563-2586．

[7] 张宝裕,刘恒基．磁场的产生．北京:机械工业出版社,1987:17-18．

[8] 雷银照．轴对称线圈磁场计算．北京:中国计量出版社,1991:135-136．

[9] 李秀芳,刘力真．一种具有均匀梯度磁场源的研究．西北建筑工程学院学报,1995(4):50-54．

[10] 王刚,安琳．COMSOL Multiphysics工程实践与理论仿真:多物理场数值分析技术．北京:电子工业出版社,2012．

Design of Magnetic Sensor Calibration Device with High Uniformity Based on Internal Series Method

JIN Duo,CHENG De-fu,WANG Yan-zhang,ZHOU Zhi-jian

(College of Instrumentation and Electrical Engineering,Jilin University,Changchun 130061,China)

Maxwell coil cannot calibrate the magnetic sensor when the high uniformity of magnetic gradient is required and the space size is strictly limited．To solve this problem,a magnetic gradient coil with high uniformity was designed as magnetic sensor calibration device．Internal series method was used to analyse the magnetic field that a single axial symmetric coil generated,and the general characteristics of the magnetic gradient field distribution were got．On this basis,the structural parameters and the uniformity of magnetic gradient coil with high uniformity were calculated．Simulation analyses were carried out on the coil model and the design and production of magnetic gradient coil device were finished．Finally,the data obtained from actual measurement and simulation proved the correctness of the design．

magnetic sensor;internal series method;uniformity;calibration;simulation

2014-03-22 收修改稿日期：2014-10-08

TM937．1

A

1002-1841(2015)03-0036-03

金多(1989—)，硕士研究生，主要研究方向为磁传感器的数字化与标定技术，E-mail:jinduo100000@126．com 程德福(1959—)，教授，博士生导师，主要研究方向为弱信号检测、地下信息探测仪器，E-mail: chengdefu@jlu．edu．cn