Classification of Precipitation Types Using Fall Velocity–Diameter Relationships from 2D-Video Distrometer Measurements

Jeong-Eun LEE,Sung-Hwa JUNG,,Hong-Mok PARK,Soohyun KWON, Pay-Liam LIN,and GyuWon LEE∗,

1Department of Astronomy and Atmospheric Sciences,Research and Training Team for Future Creative Astrophysicists and Cosmologists,Kyungpook National University,Korea

2Center for Atmospheric Remote Sensing,Kyungpook National University,Korea

3Departmentof Atmospheric Sciences,NCU,Taipei

Classification of Precipitation Types Using Fall Velocity–Diameter Relationships from 2D-Video Distrometer Measurements

Jeong-Eun LEE1,Sung-Hwa JUNG1,2,Hong-Mok PARK2,Soohyun KWON1, Pay-Liam LIN3,and GyuWon LEE∗1,2

1Department of Astronomy and Atmospheric Sciences,Research and Training Team for Future Creative Astrophysicists and Cosmologists,Kyungpook National University,Korea

2Center for Atmospheric Remote Sensing,Kyungpook National University,Korea

3Departmentof Atmospheric Sciences,NCU,Taipei

Fall velocity–diameter relationships for four different snowflake types(dendrite,plate,needle,and graupel)were investigated in northeastern South Korea,and a new algorithm for classifying hydrometeors is proposed for distrometric measurements based on the new relationships.Falling ice crystals(approximately 40 000 particles)were measured with a two-dimensional video disdrometer(2DVD)during a winter experiment from 15 January to 9 April 2010.The fall velocity–diameter relationships were derived for the four types of snowflakes based on manual classification by experts using snow photos and 2DVD measurements:the coefficients(exponents)for different snowflake types were 0.82(0.24)for dendrite, 0.74(0.35)for plate,1.03(0.71)for needle,and 1.30(0.94)for graupel,respectively.These new relationships established in the present study(PS)were compared with those from two previous studies.Hydrometeor types were classified with the derived fall velocity–diameter relationships,and the classification algorithm was evaluated using 3×3 contingency tables for one rain–snow transition event and three snowfall events.The algorithm showed good performance for the transition event: the critical success indices(CSIs)were 0.89,0.61 and 0.71 for snow,wet-snow and rain,respectively.For snow events, the algorithm performance for dendrite and plate(CSIs=1.0 and 1.0,respectively)was better than for needle and graupel (CSIs=0.67 and 0.50,respectively).

snowflake types,wet snow,fall velocity–diameter,hydrometeor type classification,2DVD

1.Introduction

Snowfall can cause damage to life and property during winter.However,the accurate measurement and prediction of ground snowfall is difficult due to wind-driven horizontal movement of snowflakes,and to the large variability in particle density as a function of the vertical structure of humidity (degree of supersaturation)and air temperature(Roebber et al.,2003;Baker et al.,2012;Nitu,2013).To accurately estimate the amount of snowfall on the ground,previous studies have been carried out using radar measurements with high spatial and temporal resolutions(e.g.Fujiyoshi et al.,1990; Matrosov,1992,1998;Huang et al.,2010).However,it is evident that the accuracy of radar-based snowfall estimations is mainly affected by the radarmeasurementheight,wind shear, and radar reflectivity–snowfall rate relationships(Z–S relationships),which depend on the size,shape,fall velocity and density of the snowflakes(Fujiyoshi et al.,1990;Matrosov, 1992,1998;Rasmussen et al.,2003).The fall velocity of snowflakes plays a particularly significant role in governing the trail of snowfall,and in representing the density of snow and microphysical processes.Therefore,research on the relationship between the size and fall velocity of snowflakes is essential for the accurate estimation of snowfall amount.

Langleben(1954)suggested that melting or riming processes were the main causes of an increase in snowflake fall velocity,and derived fall velocity–diameterrelationships(V–D relationship)according to snowflake types.Hansch(1999) investigated variables governing fall velocity(e.g.,vertical size,area of perpendicular circumscribed circle,and the area ratio between the cross-sectional area and the circumscribed ellipse area)based on a theoretical approach,and conducted experiments using 2D Video Disdrometer(2DVD)measure-ments;thestudysuggestedvariousV–Drelationshipsaccording to snowflake type and degree of riming.It is of note that the variability of coefficients in V–D relationships is greater for the degree of riming than for snowflake types.

Barthazy and Schefold(2006)(BS hereafter)presented power-law and exponential V–D relationships for various snowflake types according to the degree of riming(classes 0–5),which is proportional to the coverage ratio of a droplet on a snowflake’s surface,using a Hydrometeor Velocity and ShapeDetector(HVSD).Intheirstudy,theV–Drelationships were relatively independent of the degree of riming in weak riming stages(classes 1–3),whereas the relationships varied significantly with the degreeof rimingin heavy riming stages (classes 3–5).Zawadzki et al.(2010)investigated the variability and uncertainties in snowfall velocity measurements that occurred when using an HVSD,such as instrument uncertainty in the fall velocity measurement,the effect of wobbling snowflakes on the accuracy of velocity measurements, and naturalvariabilityin the homogeneoussnow terminal fall velocity.They also analyzed the correlations of the coefficients of V–D relationships with surface temperature,the temperature at echo top,and vertical depth of the precipitation system,all of which were derived using aircraft soundings and a vertically pointing X-band radar.

Yuter et al.(2006)used the Particle Size and Velocity(PARSIVEL)to present various two-dimensional distributions between the size and fall velocity of rain,mixedphase precipitation(rain and wet snow),and dry snow,and suggested a classification technique for mixed precipitation. Sheppard and Joe(2000)compared automatic measurements from various sensors[Vaisala FD12P,HSS Model 402B, WeatherIdentifierandVisibilitySensor(WIVis),andthePrecipitation Occurrence Sensor System(POSS)]with manned observations,and then presented the limitations of each sensor.Grazioli et al.(2014)developedthe hydrometeorclassif ication method using 2DVD measurements based on the support vector machine method.In addition,dual-polarization weather radar has been recently used to classify hydrometeor types(e.g.Vivekanandan et al.,1999;Liu and Chandrasekar, 2000;Lim et al.,2005;Park et al.,2009).The hydrometeor classification algorithm utilizes a fuzzy logic approach to combine feature parameters by employing polarimetric radar measurements(horizontal reflectivity,differential reflectivity,differential propagation phase shift,correlation coef ficient,and linear depolarization ratio),and then classi fies various hydrometeor types(such as drizzle,rain,dry snow, wet snow,hailstone,graupel).Furthermore,Moisseev et al. (2009)showed that dual-polarization radar is a useful tool for identifying the growth processes of snowflakes,such as aggregation,riming,and deposition.

This study aims to derive new V–D relationships according to snowflake types in Korea,and to develop a new hydrometeor classification algorithm based on the derived relationships using 2DVD measurements.The paper is presented as follows:2DVD measurements and snowflake photographs used in this study are described in section 2.The quality control process of the 2DVD measurements,and the procedures used to derive the V–D relationships and to develop the hydrometeor classification algorithm are explained in section 3. Insection4,thenew V–Drelationshipsarecomparedwith results fromthepreviousstudies ofBS andLocatelliandHobbs (1974)(LH hereafter),and the Hydrometeor Classification Algorithm(HCA)is evaluated.Section 5 then summarizes the processes and results of this study.

2.Data

2DVD data and close-up pictures of snowflakes collected at the Cloud Physical Observation Station[CPOS,(37◦41′N, 128◦45′E),842 m MSL]from 15 January to 9 April 2010 were analyzed.2DVD instruments provided various details of precipitation particles(e.g.,fall velocity,equivalent volume spherical diameter,major and minor axes,and canting angle)using two light sheets(with widths of 10 cm containing 512 pixels each)that are transmitted from two orthogonal light sources to the line scan cameras(which can capture the shadows of a particle)on a horizontal plane(see Fig.1).The two light sheets were placed at a vertical distance of 6.2 mm from each other,creating a virtual measuring area of 10 cm ×10 cm.The captured images then entered the image processingprocedureofthe2DVD,whichintegratesinformation received from each line-scan camera in relation to the particles.The fall velocity and equivalent volume spherical diameter were then estimated for particles that fell into the virtual measuring area only(Kruger and Krajewski,2002;Schonhuber et al.,2008).

Snowflakes were photographed using a high-resolution digital camera system every 10 min after collection,by means of a rectangular-shaped collection plate with a size of 21.0 cm×29.7 cm(623.7 cm2)that was covered with black velvet to alleviate particle breaking(Fig.2).This plate was exposed to snowfall for approximately 2–5 s,depending on the snowfall intensity.The snowflakes that collected on the plate were then moved into a dark room,where the intensity of illumination was steadily maintained,and the temperature was maintained close to that of the temperature outdoors,to avoid melting the snowflakes.Snowflake photographs were taken using a Nikon D80 Digital Single Lens Reflector camera with a high resolutionof 3872×2592pixels,a fixed focal length of 60 mm,an exposure time of 1/30 s,and a focallength-aperture ratio of F3.8(Fig.2).

To derive the V–D relationships for the various types of snow particles,the 2DVD measurements were classified into four different snowflake types(dendrite,plate,needle, and graupel),based on the dominant snowflakes present after photo-interpretation(Figs.2c–f),as determined by experts analyzing the silhouettes of snowflakes on the x–z or y–z planeofthe 2DVD.Anyambiguousand/ormixed-phased events were excluded(Fig.2b)from the dataset.If one of the snowflake types accounted for more than at least 70%of all snowflake types in the photograph,it was determined to be the dominant snowflake type.Therefore,even if it is possible to roughly identify the snowflake type using photographs taken of large collections of snowflakes,habit identification is effective.However,sucha meansofidentificationhaslimitations because each size of snowflake and its velocitycannot be determined.

The periods during which the 2DVD measurements were obtained to derive the V–D relationship for each type of snowflake is listed in Table 1.The number of each snowflake type counted was 2754 for dendrite,824 for plate,23 584 for needle,and 6698 for graupel.In addition,to evaluate the HCA,a rain–snowtransition event(9 February2010)andthree snow events(12 February,15 February,and 4 March 2010)were used(Table 2).

3.Methodology

3.1.Quality control of 2DVD data

The quality control procedure used in relation to 2DVD data consisted of two steps.The first step employed 2DVD software to remove mismatched particles caused by contamination,such as the overlap of snow particles in the line of sight and particles crossing the virtual measuring area,in addition to the aerodynamics effects related to the 2DVD,tumbling snowflakes,and side views of snowflakes that were significantly different(particularlyneedle-type).This used individual information related to particles captured by the upper and lower line-scan cameras(Hansch,1999;Krugerand Krajewski,2002;Huang et al.,2010).The following particles were eliminated by quality control:fall velocity＞4 m s−1or diameter＜0.2 mm.In addition,particles that were shown to have significantly different areas in the images taken between one camera and another were eliminated.This quality control may eliminate particles that have very different areas from two cameras,although real snow particles can exhibit different shapes from different view angles.However,these particles may lead to significant errors in the velocity measurements.

In BS,the V–D relationships for four snowflake types (dendrite,plate,needle,and irregular crystals including graupel)were derived based on the degree of riming obtained by using the HVSD at different altitudes.In the present study (PS),the diameter of the precipitation particles was defined as the equivalent diameter of particles as captured by the two line cameras in the 2DVD instruments,whereas the maximum diameter of precipitation particles captured by two parallel beams from HVSD was used in BS.Therefore,the difference in the diameter definitions gives rise to some differences between PS and BS.

To derive accurate V–D relationships,minor types of snowflakeswereremovedfromtheraw2DVDdata.Themost probable velocity and its standard deviation(σ)were calculated with a diameter interval of 0.2 mm,and any particles that crossed±σfrom the most probable velocity were then removed.Figure 3 shows an example of the quality control used for the 2DVD measurements obtained from 1618 UTC to 1623 UTC 15 February 2010.The scatter plot between the fall velocity and diameter of raw 2DVD measurements is described in Fig.3a,and Fig.3b shows the distribution after removing mismatched and ambiguous particles.In this example,mismatched particles were mostly distributed at diameters of less than 1.0 mm,and minor types of snowflakes were then removed using a threshold of one standard deviation from the most probable velocity(Fig.3c).

For a rainfall event,particles that were beyond the followingrangewereidentifiedas mismatchedparticles(Kruger and Krajewski,2002)and thus removed:

whereVmeasured(units:m s−1)is the velocitymeasured by the 2DVD,andVAindicates the calculated velocityfromthe V–D relationship(V=9.65−10.3e−0.6D)for raindrops(Atlas et al.,1973,hereafter AT73).

3.2.Derivation of V–D relationships

The V–D relationships for various snowflake types were derived by the power-law regression as follows:

where a and b are coefficients,and D and V(D)represent the diameter(mm)and the fall velocity(m s−1),respectively. Since power-law relationships are simple and useful in determining the analytic solution of a model(e.g.for Dopplerspectra calculations),they are mostly used to derive the V–D relationship for snow particles(Langleben,1954;Hansch, 1999;Zawadzki et al.,2010).In this study,the V–D relationships were derived using the weighted total least squares (WTLS)fitting method(Amemoya,1997)rather than the ordinary least squares fitting method,as the WTLS method is able to minimize both uncertainties in the diameter,as well as in the fall velocity of 2DVD measurements,unlike the ordinary least squares fit.

3.3.Algorithm for hydrometeor classification

The proposed HCA classifies the hydrometeor into six particle types(rain,wet snow/sleet,and the snowflake types of dendrite,plate,needle,and graupel),based on the AT73 relationship for raindrops and the newly proposed relationships for four different types of snowflakes.To classify the hydrometeor types,the HCA utilizes the difference between the velocity[Vj(Dobs,i)]from empirical relationships and the measured velocity(Vobs,i)from the 2DVD as follows:

where Dobs,iand Vobs,iare the diameter and velocity of each particle measured by 2DVD within a given time window (e.g.,5 min);j indicates the hydrometeor type(rain,or the snowflake types of dendrite,plate,needle,and graupel);and N is the total number of particles.Thus,five fjare calculated for a time window of 5 min.

Figure 4 shows a flow chart of the HCA.The theoretical fall velocity[Vj(Dobs,i)]at a given diameter was firstly calculated from the V–D relationships for each hydrometeor type. The averaged absolute value(fj)of the difference between the theoretical fall velocity from the V–D relationship and the measured velocity from the 2DVD were then calculated using Eq.(3).When the minimum value(fj,min)among the calculated fjwas less than the threshold(fthreshold),the subscript j was finally identified as one of the hydrometeortypes (e.g.,rain,or the snowflake types of dendrite,plate,needle, or graupel);otherwise,it was classified as wet snow/sleet.

4.Results

4.1.V–D relationships of snowflake types

Figure 5 shows the two-dimensional normalized frequency distribution between the fall velocity and diameter in the 2DVDmeasurements,according to the type ofsnowflakes based on photo-interpretation by human experts.Class intervals for the diameter and fall velocity were 0.1 mm and 0.1 m s−1,respectively.The solid line shown in Fig.5 represents the V–Drelationship fitted by the WTLS method.The fall velocities of both dendrite and plate are distributed in the range from 0.6 to 1.3 m s−1.The diameter of dendrite has a rangefrom 0.0 to 4.0 mm,with a relatively high frequency at diameters＜1.5 mm(Fig.5a),whereas that of plate is confined to less than around 2.0 mm.The exponents and coefficients in the V–D relationship are 0.82 and 0.24 for dendrite,and 0.74 and 0.35 for plate,respectively.However,their fall velocities tend to remain almost constant(between 0.6 and 1.3 m s−1),with a small exponent(＜0.4)and coefficient(＜1.0), due to their low densities and flat-snowflake shapes.The exponent of dendrite is particularly small,which indicates that the growth of dendrite was by aggregation and deposition, causing an increase in size but no significant change in density.

The diametersof needleandgraupelrangefrom0.0to 4.0 mm,and are mostly concentratedat diameters under 1.5 mm; the range of their fall velocities(0.6–2.2m s−1)is wider than that of dendrite and plate(0.6–1.3 m s−1).While the diameter ranges of both needle and graupel are similar to that of dendrite,their fall velocities increase more rapidly than that of dendrite,with increasing diameters.This indicates that the needle-typeparticles developedundera rimingregime,as the rimingprocess usuallycausesthe fall velocityto increasesignificantly.Furthermore,weak aggregated or rimed needles were frequently observed during the photo-interpretation in thefield(Fig.2e).Inaddition,the graupel-typeparticleswere a result of significant riming,which caused such a change in the originalshape of the snowflake that it was no longer identifiable.Therefore,the coefficients and exponents of both the needle(1.03and0.71,respectively)andthe graupel(1.30and 0.94,respectively)in the V–D relationships were larger than those of both the dendrite and plate.

The averaged difference(fj)between fall velocities calculated from the V–D relationship and 2DVD measurements was calculatedbyEq.(3),accordingto thehydrometeortype. The value of fjfor dendrite,plate,needle and graupel were 0.10,0.05,0.21 and 0.18 m s−1,respectively.In addition,the value of fjfor raindrop(0.41)was calculated by comparing with the V–D relationship(AT73)for rainfall events occurring g on 8 February 2010(not shown).

4.2.Comparison with previous studies

For a comparison of the V–D relationships between PS and BS,the fall velocities in the V–D relationships were converted into at mean sea level(MSL)(1013 hPa)using Eq. (4),which requires consideration of the effect of air density changes due to differences in observing altitudes(Brandes et al.,2008):

whereVobsandV1013,expressedin m s−1,indicate the fall velocity of each snowflake at observational altitude and MSL, respectively;ρ1013(1.225 kg m−3)andρobs(1.112 kg m−2) refer to the density of air at 1013 hPa and at an observational altitude(842 m MSL),where the air density is linearly in-terpolated in the vertical direction based on the air density profile of the standard atmosphere.In BS,the fall velocity of snowflakes was measured at an altitude of 1604 m MSL and aρobscorresponding to 1.048 kg m−3.

Table 3 and Fig.6 illustrate the V–D relationships corresponding to snowflake types in PS(solid lines)and BS (dashed lines),both after and before applying a height reduction to obtain values corresponding to those at MSL,and in LH(dashed lines).The results of LH are mostly used as a reference in the community,although in their study the authors did not report temperatures and the pressure conditions whenmeasuringthe fall velocity.Thedifferencein the observational height between PS and BS does not cause a differenceinthevalueoftheexponentsbetweenV–Drelationships. Four types of snowflakes show similar trends in terms of the V–D relationships.In PS and BS,the V–D relationship for dendrite(graupel)is gentlest(steepest).Thecoefficientofthe adjusted V–D relationship for dendrite in PS(0.79)is smaller than that in BS(0.91 for moderately rimed dendrite and 0.98 for densely rimed dendrite)and is close to that of LH(0.80 for unrimed dendrite and 0.79 for densely rimed dendrite),as shown in Table 3.The exponent for dendrite in PS(0.24)is equal to that for denselyrimed dendritein BS,and is between that of unrimed(0.16)and densely rimed dendrite(0.27)in LH.On the contrary,the coefficient for plate in PS(0.71)is smaller than that in BS(that for unrimed,moderately rimed, anddenselyrimedplateare0.94,1.12and1.26,respectively), and its exponent in PS(0.35)is between that of moderately rimed(0.26)and densely rimed plate(0.40)in BS.The coefficient for needle in PS(0.99)is between that for unrimed (0.90)and moderately rimed needle(1.17)in BS,and the exponent for needle in PS(0.71)is greater than that for densely rimed needle(0.35)in BS.Furthermore,the coefficient for graupel in PS is smaller(greater)than that for graupel in BS(LH),and its exponent in PS is greater than that in BS (0.61)and LH(range between 0.28 and 0.65).The temperature range for graupel is−1.2◦C to−1.0◦C in PS,whereas BS reported a temperature range of−5.0 to−1.0◦C for the 15 cases.Assuming the temperature for graupel is colder in BS than in PS,the density of graupel would be higher in PS than in BS(Garrett and Yuter,2014),and thus the difference in power-law exponentsbetween PS and BS would be caused by the differences in temperature.

Fortheentirerangesofdiameters,thefall velocityofdendrite and plate in PS is smaller than that of dendrite and plate in BS,as shown in Fig.6,and,in addition,the fall velocity of needle and graupel in PS is smaller than that of needle and graupel in BS,with a range in diameter of＜approximately 1.5 mm.However,the fall velocity of needle and graupel in PS is greater than that of needle and graupel in BS,with a range in diameter of＞1.5 mm,and the fall velocity increases more rapidly with increasing diameter than in BS.The V–D relationship of needle and graupel with increasing diameter in PS intersects that of needle and graupel in BS.

4.3.Classification of hydrometeor types using the V–D relationship

4.3.1.Rain–snow transition case

The performance of the HCA was examined using a transition case(between rain and snow on 9 February 2010),as shown in Table 2.Equations(10)to(13),given in Table 3, were applied as the reference V–D relationship corresponding to the type of snowflake in the HCA,and AT73 was used as the reference V–D relationship for raindrops.

The two-dimensional distribution between the fall velocity and diameter corresponding to the precipitation types in the 2DVD measurements was investigated(Fig.7)prior to a performance test of the HCA.The class intervals in the twodimensional normalized frequency distribution were 0.1 mmand 0.1 m s−1,as shown in Fig.7.The solid line refers to AT73,and the blue,red,purple and green dashed lines represent the V–D relationship for the snowflake types of dendrite, plate,needle and graupel,respectively,in this study.

Table 3.Comparison of V–D relationships between this study and previous studies.

Results show that,although AT73 was slightly higher than the measured fall velocity overthe entire diameterrange, the fallvelocity ofraindropsin 2DVDagreed wellwith AT73. In addition,the V–D relationship for raindrops increased remarkably as its diameterincreased(Fig.7a).In thisstudy,the fall velocity of snowflakes(needle)increased less remarkably than that of raindrops with increasing diameter,according to the V–Drelationship forneedle(Fig.7b).Forwetsnow/sleet, the fall velocity was widely distributed between the V–D relationships of raindrops and graupel(Fig.7c).The V–D relationship of considerably(relatively)melted small(large)ice crystals was particularly close to AT73(apart from the V–D relationship of graupel).Hence,an optimal V–D relationship for wet snow/sleet was impossible to derive,due to the large variation in fall velocity,which depends on the ratio between the water and ice contents in the precipitation particles.Thurai et al.(2007)found similar results,i.e.,that the fall velocity and diameter data from 2DVD deviated slightly from the Gunn–Kinzer(G–K)curve during a period of rain,while the fall velocities distributed below the G–K curve in the case of wet snow,and the fall velocities of dry snow were less than about 2.8 m s−1.

In the HCA,wet snow/sleet can be classified based on the difference in the V–D relationships of raindrops and snowflakes.The value of fj,0.60,applied as a threshold, is larger than the maximum fj(0.41)among the values of fjfor the five hydrometeor types(raindrop,and the snowflake types of plate,dendrite,needle,and graupel)in the previous section.In other words,if the minimum fjis larger than 0.6, the event can be classified as a wet snow/sleet event.

Figure 8 illustratesthe time seriesoffive fjs derived from the HCA and the final classification by applying the threshold value of 0.6 for the transition case of rain and snow on 9 February 2010.The reference classification of hydrometeor types based on photo-interpretation and 2DVDmeasurements by experts is presented in the upper part of Fig.8b.

For a quantitative evaluation of the HCA’s performance, it is necessary to predetermine the reference classification by using the particle shape from 2DVD measurements and from the photo-interpretation by human experts.The hydrometeor types were classified into raindrop,wet snow/sleet,and snowflakes(dendrite,plate,needle,and graupel).The performance of the HCA was then evaluated using three skill scores(probability of detection,POD;false alarm ratio,FAR; critical success index,CSI)derived from the 3×3 contingency table for three categories(raindrop,wet snow/sleet, and snowflakes)(Wilks,2006,Fig.9).The symbol“O”implies the reference hydrometeor types determined by human experts,and“P”stands for the hydrometeor types classified with the HCA in Fig.9.Moreover,“r”–“z”represents thenumber of classifications for each type category;for example,“r”and“u”represent the number of rainfall events that are classified by the HCA correctly asraindrop events,and incorrectly as wet snow/sleet events,respectively.To derive the skill score for individual precipitation types,the 3×3 contingency table was reduced to 2×2(Fig.9),and the performance was then evaluated by using the score of the three skills(POD,FAR,and CSI),as follows:

where e is the numberofwet snow/sleet events correctly classified by the HCA;f is the numberof othereventsincorrectly classified;and g is the numberofwet snow/sleet eventsincorrectly classified as other types by the HCA.

The skill scores according to the type of precipitation are listed in Table 4.PODs for both raindrops and wet snow/sleet(0.90)are larger than that of snow(0.71).The low skill score for snow is due to the large variation in the fall velocity of snowflakes,and hence snowflakes with a large fall velocity are incorrectly identified as wet snow.The FAR of wet snow/sleet(0.35)is larger than that of rain(0.03)and snow(0.00).Precipitation types were mostly misclassified during transition periods(e.g.,snow to wet snow/sleet,wetsnow/sleet to rain,etc.),due to the large variations in velocities during transitions.The CSI of wet snow/sleet(0.61)is smaller than that of rain(0.89)and snow(0.71).

4.3.2.Snowfall case

The performance of the HCA for four snowflake types (dendrite,plate,needle,and graupel)was evaluated by comparing with photo-interpretation by human experts using the snowfall cases(cases 2–4)listed in Table 2.Representative examples are shown in Fig.10.

The skill scores for four snowflake types are listed in Table 5.POD,FAR,and CSI for dendrite were 1.00,0.00, and 1.00,respectively,and for plate were 1.00,0.00,and 1.00,respectively.All the dendrite and plate of snowflakes were,therefore,correctly classified.The POD,FAR,and CSI for needle were 0.67,0.00,and 0.67,respectively.CSI and POD of needle were relatively smaller than those of dendrite and plate because the coefficient and exponent values of the V–D relationship for needle were between those of graupel and dendrite,and because the fall velocity of needle may strongly depend on the degree of riming under different growth regimes.The POD of graupel was 1.00,and its CSI was smaller than that of the other snowflake types due to its high FAR(0.50).The misclassification of needle to graupel in the HCA results with a high value of FAR is considered to have occurred because the fall velocity of densely rimed needle may be similar to that of graupel.

5.Summary and conclusion

The V–D relationships by snowflake type were derived, and the HCA was developedusing snow particle photographs taken at intervals of 10 minutes and 2DVD measurements at CPOS from 9 January to 9 April 2010.

在大数据时代下，数据激增对数据处理的精确性和实效性等都提出了更高的标准，新型电网规划体系获取数据的主要方法是结合无人机、卫星遥感等先进的技术来获取数据。无人机、卫星遥感等技术的发展日

Mismatched and/or minor-type particles were removed during the quality control procedure.The V–D relationships for four snowflake types(dendrite,plate,needle and graupel) were derived from 2DVD measurements based on photointerpretations by human experts.Finally,a classification algorithm for six precipitation particles,including raindrops and wet snow/sleet,was developed using the 2DVD measurements.The HCA is based on the difference between the fall velocity from the predetermined V–D relationship for a given diameter and that of particles captured by 2DVD.For the classification of raindrops,AT73 was applied,and wet snow/sleet was classified using the threshold value of the averaged difference of fall velocities.

The fall velocities of dendrite and plate were narrowly ranged between 0.6 and 1.3 m s−1and slowly increased with increasing diameter due to the aerodynamic effects caused by their low density and flat shapes.Note that the diameter range of dendrite(0.0–4.0 mm)was twice as large as that of plate(0.0–2.0 mm),whereas both snowflakes had a similar fall velocity.It is considered that,in this study,dendrite grew under aggregation and deposition regimes.In addition,the fall velocities of needle and graupel were distributed within a range of 0.6–2.2 m s−1,and had a larger range than those of dendrite and plate.The coefficient and exponent of both needle and graupel were larger than those of dendrite;that is, the fall velocity of needle and graupel increased more rapidly with increasing diameter than that of dendrite,due to growth under riming regimes.

The derived V–D relationships were adjusted with respect to the reference height(1013 hPa)and,then,compared with the V–D relationships in BS.The fall velocities of both dendrite and plate in this study were consistently smaller than those of BS over the whole diameter range;for needle and graupel,the fall velocities in this study increased more rapidly with increasing diameter than those of BS.It is considered that instrumental and geographical differences may have caused the discrepancy of the V–D relationships between the two studies.

We then calculated the averaged difference between the fallvelocities,whichwerecalculatedusingempiricalV–Drelationships and observed 2DVD measurements according to hydrometeortype.The averageddifferencesof the fall velocities accordingto hydrometeortypewereusedtodiscriminate wet snow/sleet from other hydrometeortypes.The HCA was applied to alternating transition cases of snow and rain.It was found that the fall velocity of wet snow/sleet varied significantly according to the ratio of air and water in particles. Therefore,it is impossible to determine an optimal,single V–D relationship for wet snow/sleet that can be discriminated from other hydrometeor types,based on the minimum average difference(fj)between the fall velocity derived from the V–D relationship and the fall velocity measurements.In this study,a threshold value of fj,0.6,was used to identify wet snow/sleet.

We then evaluated the performance of the HCA using the skill scores from a 3×3 contingency table.The CSI for raindrops(0.89)and snow(0.71)was larger than that for wet snow/sleet(0.61).However,the FAR for wet snow/sleet (0.35)was larger than both rain(0.03)and snow(0.00).The V–D relationship of needle was located between that of den-drite and graupel,and the POD and CSI(0.67 and 0.67)of needle were smaller than those(1.00 and 1.00)of both dendrite and plate due to fluctuationsin the fall velocitybased on the degree of riming of needle.The CSI of needle(0.5)was the smallest.

Table 4.Skill scores for rain,wet snow,and snow precipitation types.

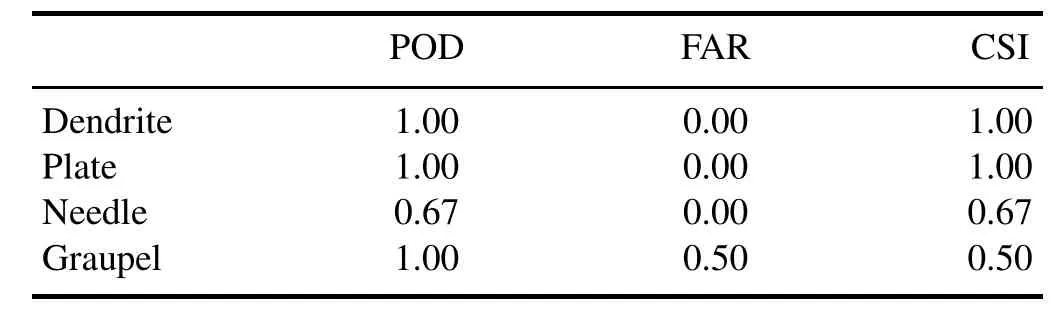
Table 5.Skill scores for dendrite,plate,needle,and graupel snowflake types.

Yuteret al.(2006)suggestedaclassification algorithmfor precipitation particles based on the fall velocity and diameter of particles.However,this algorithm can only distinguish snow from rain and mixed rain using a two-dimensional frequencydistribution,whichisnotsuitableforsnowflaketypes. In contrast,our HCA is able to classify hydrometeorsinto six different types of precipitation:rain,wet snow/sleet,and the snowflake types of dendrite,plate,needle,and graupel.

ThederivedV–Drelationshipsinthisstudycanbeusedas a reference relationship for snowfall events over the Korean peninsula and,in addition,the HCA can be utilized for future studies related to snowfall estimation and V–D relationships. However,it is considered that the classification of precipitation particles needs to be further categorized by taking into consideration the growth regime of precipitation particles.In addition,our HCA could be further improved by considering surface temperature,or by using the vertical profile of temperature from a model.

Acknowledgements.The efforts of You Yu MAO and Y.R CHEN at the NCU in Taipei in setting up and maintaining the2DVD are gratefully acknowledged.The hard work of junior scientists Kwang-Deuk AHN and Yo-Han CHO at the National Institute of Meteorological Research and Young-A OH,Su-Hyang LEE,and Jun-Youn JUNG during the collection of high-quality field data is greatly appreciated.This work was funded by the Korea Meteorological Administration Research and Development Program under Grant KMIPA2015-1010.

REFERENCES

Amemoya,Y.,1997:Generalization of the TLS approach in the errors-in-variables problem.Proc.the Second International Workshop on Recent Advances in Total Least Squares Techniques and Errors-in-Variables Modeling,S.Van Huffel,Ed., SISM,77–86.

Atlas,D.,Srivastava,R.C.and Sekhon,R.S.,1973:Doppler radar characteristicsof precipitation at vertical incidence.Rev.Geophys.Space Phys.,11,1–35.

Baker,B.,and Coauthors,2012:How well are we measuring snow?The NOAA/FAA/NCAR winter precipitation test bed. Bull.Amer.Meteor.Soc.,93,811–829.

Barthazy,E.,and R.Schefold,2006:Fall velocity of snowflakes of different riming degree and crystal types.Atmospheric Research,82,391–398.

Brandes,E.A.,K.Ikeda,G.Thompson,and M.Sch¨onhuber,2008: Aggregate terminal velocity/temperature relations.J.Appl. Meteor.Climatol.,47,2729–2736.

Fujiyoshi,Y.,T.Endoh,T.Yamada,K.Tsuboki,Y.Tachibana,and G.Wakahama,1990:Determination of a Z-R relationship for snowfall using a radar and high sensitivity snow gauges.J. Appl.Meteor.,29,147–152.

Garrett,T.J.,and S.E.Yuter,2014:Observed influence of riming, temperature,and turbulence on the fallspeed of solid precipitation.Geophys.Res.Lett.,41,6515–6522.

Grazioli,J.,D.Tuia,S.Monhart,M.Schneebeli,T.Raupach, and A.Berne,2014:Hydrometeor classification from twodimensional video disdrometer data.Atmos.Meas.Tech.,7, 2869–2882.

Hansch,M.,1999:Fall velocity and shape of snowflakes.Ph.D. thesis,Swiss Federal Institute of Technology,117 pp.

Huang,G.-J.,V.N.Bringi,R.Cifelli,D.Hudak,and W.A.Petersen,2010:A methodology to derive radar reflectivityliquid equivalent snow rate relations using C-Band radar and a 2D video disdrometer.J.Atmos.Oceanic Technol.,27,637–651.

Kruger,A.,and W.F.Krajewski,2002:Two-dimensional video disdrometer:A description.J.Atmos.Oceanic Technol.,19, 602–617.

Langleben,M.P.,1954:The terminal velocity of snowflakes. Quart.J.Roy.Meteor.Soc.,80,174–181.

Lim,S.,V.Chandrasekar,and V.N.Bringi,2005:Hydrometeor classification system using dual-polarization radar measurements:Model improvements and in situ verification.IEEE Trans.Geosci.Remote Sens.,43,792–801.

Liu,H.P.,and V.Chandrasekar,2000:Classification of hydrometeors based on polarimetric radar measurements:Development of fuzzy logic and neuro-fuzzy systems,and in situ verification.J.Atmos.Oceanic Technol.,17,140–164.

Locatelli,J.D.,and P.V.Hobbs,1974:Fall speeds and masses of solid precipitation particles.J.Geophys.Res.,79,2185–2197.

Matrosov,S.Y.,1992:Radar reflectivity in snowfall.IEEE Trans. Geosci.Remote Sens.,30,454–461.

Matrosov,S.Y.,1998:A dual-wavelength radar method to measure snowfall rate.J.Appl.Meteor.,37,1510–1521.

Moisseev,D.,E.Saltikoff,and M.Leskinen,2009:Dualpolarization weather radar observations of snow growth processes.34th Conference on Radar Meteorology,Williamsburg,VA,Amer.Meteor.Soc.,13B.2.

Nitu,R.,2013:Cold as SPICE.Meteorological Technology International,148–150.

Park,H.S.,A.V.Ryzhkov,D.S.Zrni´c and K.-E.Kim,2009: The hydrometeor classification algorithm for the polarimetric WSR-88D:Description and application to an MCS.Wea. Forecasting,24,730–748.

Rasmussen,R.,M.Dixon,S.Vasiloff,F.Hage,S.Knight,J. Vivekanandan,and M.Xu,2003:Snow nowcasting using a real-time correlation of radar reflectivity with snow gauge accumulation.J.Appl.Meteor.,42,20–36.

Roebber,P.J.,S.L.Bruening,D.M.Schultz,and J.V.Cortinas Jr.,2003:Improving snowfall forecasting by diagnosing snow density.Wea.Forecasting,18,264–287.

Schonhuber,M.,Lammer,G.,and Randeu,W.L.,2008:The 2DVideo-Distrometer.Precipitation:Advances in Measurement, Estimation,and Prediction,S.Michaelides,Ed.Springer,3–31.

Sheppard,B.E.,and P.I.Joe,2000:Automated precipitation detection and typing in winter:A two-year study.J.Atmos. Oceanic Technol.,17,1493–1507.

Thurai,M.,D.Hudak,V.N.Bringi,G.W.Lee,and B.Sheppard, 2007:Cold rain event analysis using 2-D video disdrometer,C-band polarimetric radar,X-band vertically-pointing radar and POSS.Preprints,33rd Conf.on Radar Meteorology,Cairns,Australia,Amer.Meteor.Soc.,P10.5.[Available online at http://ams.confex.com/ams/pdfpapers/123455.pdf.]

Vivekanandan,J.,S.Ellis,D.Oye,D.S.Zrnic,A.V.Ryzhkov, and J.Straka,1999:Cloud microphysics retrieval using S-band dual-polarization radar measurements.Bull.Amer.Meteor.Soc.,80,381–388.

Wilks,D.,2006:Statistical methods in the atmospheric sciences, 2nd ed.,Academic,Burlington,Mass,627 pp.

Yuter,S.E.,D.E.Kingsmill,L.B.Nance,and M.Loffler-Mang, 2006:Observations of precipitation size and fall speed characteristics within coexisting rain and wet snow.J.Appl.Meteor.Climatol.,45,1450–1464.

Zawadzki,I.,E.Jung,and G.Lee,2010:Snow Studies.Part I:A study of natural variability of snow terminal velocity.J.Atmos.Sci.,67,1591–1604.

:Lee,J.-E.,S.-H.Jung,H.-M.Park,S.Kwon,P.-L.Lin,and G.-W.Lee,2015:Classification of precipitation types using fall velocity–diameter relationships from 2D-video distrometer measurements.Adv.Atmos.Sci.,32(9),1277–1290,

10.1007/s00376-015-4234-4.

26 October 2014;revised 1 March 2015;accepted 26 March 2015)

∗Corresponding author:GyuWon LEE

Email:gyuwon@knu.ac.kr