让“节外生枝”变成“精彩生成”

蔡志伟

非预设生成是指在课堂的师生互动中，学生提供的材料、学习的思维成果、学生开展实验操作获得的结果或结论，与教师的预设不一致，或在教师预想之外的学习生成。在现实的数学课堂学习中，非预设生成给课堂带来的结果往往具有两极性—尴尬或精彩，那么教师如何才能智慧地应对课堂中的非预设生成呢？笔者想结合几个案例来谈一些粗浅的想法。

案例一：老师，你的答案错了

上学期，笔者在课上曾出了这样一个题目让学生练习：已知a=，b=，请你用含a，b的代数式表示。当学生在下面完成练习后我就把自己的答案写在黑板上。

师：这题我的答案是a5b。

没想到学生马上提出质疑。

生：老师，你的答案错了，应该是4ab。

我一愣，因为我预设的答案不是4ab，但随即镇定下来，因为我的答案肯定是正确的，于是我还是很有耐性地先来了个反问。

师：（胸有成竹地微笑着）难道真的是我的答案错了？请生1同学到黑板上和老师一起把解答过程写一下，好吗？

生1： =4×=4ab.

师： ==4×=（）4××

=（）5×=a5b.

我一看到学生的答案就马上判断也是正确的，并且比我做的要简洁明了，但我还是故作镇定，索性来个借题发挥。

师：请同学们看看我的解题过程对吗？

生众：咦，老师的答案好像也是对的......

师：怎么来说明呢？

生2：从你们两位的解题过程看，都是正确的，其实4ab=，

a5b=，自然4ab=a5b。

生3：我觉得还可以这样来说明，4ab=（）4ab=a4ab =a5b。

师：都很不错啊！ 大家的答案可比老师的简单呢！

……

案例二：我发现规律了

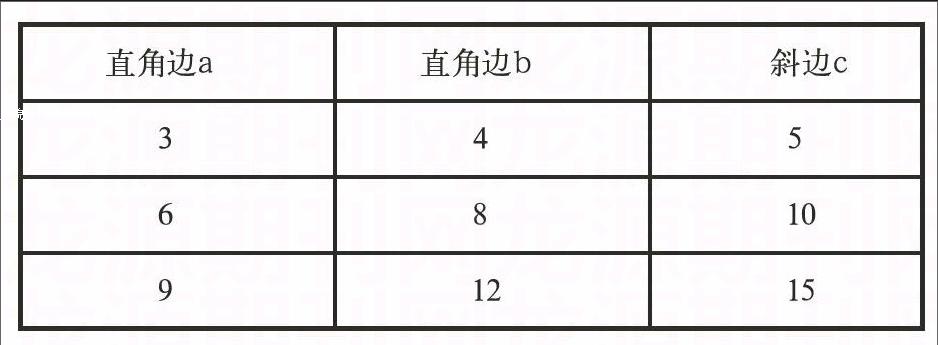
学生已经探究出了勾股定理，接下来的一个环节是要让学生来了解和研究“勾股数”，笔者给出了一组填空题。已知Rt△ABC中，∠C=90°，根据直角边求斜边c。

学生很快根据勾股定理a2+b2=c2求出c分别为5，10，15。于是我把它们填在表中，然后让学生观察思考这三组数有何联系。

生1：a、b、c三边满足勾股定理，可以直接通过a2+b2=c2求c。

生2：我觉得都满足c=2b-a，我不用勾股定理照样可以求斜边c。

我和其他学生都有点吃惊，特别是我从来没有预设过，但我马上把这个问题抛给学生。我反问学生：同学们来看看生2的做法对吗？在学生思考的间隙我快速地判断了一下，生2的回答是偏离我的问题的（当然也包括生1），但是可以认同生2的说法。事实上，学生也都认同生2的观点。

师：咱们一起来研究这个“意外”的发现，大家都认为生2的做法在这个题目中是可行的，那你能说明吗？

生2：4×2-3=5，8×2-6=10，12×2-9=15.

师：嗯，我知道你就是按这三个式子推导出c=2b-a的，我的意思是要来证明这个式子。

生3：可以设这一组数为3n，4n，5n，则4n×2-3n=5n。

师：（终于看到预设的3n，4n，5n出现了）不错啊！回过来我们再来看看3，4，5；6，8，10；9，12，15这三组数有何联系？你还能找到这样的一组数吗？

生4：第二组各数是第一组各数的2倍，第三组各数是第一组各数的3倍。可以推断，第n组数字是第一组各数的n倍。

师：像这些满足勾股定理的一组组整数数据，我们称之为“勾股数”。那是不是所有的勾股数都是有3n，4n，5n的形式或是满足生2所说的c=2b-a？

引发了学生新的认知冲突。

生5：5，12，13也是勾股数，但它不满足12×2-5=13。

生6：我算了一下，10，24，26虽然是5，12，13各数的2倍，但却不是勾股数。

……

学生的思维被完全激发了。

教学反思：

一、非预设生成的意义

1.非预设生成是学生的一种自主探究。它往往是学生不满足本课中的学习目标而对该知识作出的自主探究，这种探究冲动在课堂中得到支持与否，对学生的学习发展可谓影响深远。每位数学教师都应努力促进预设生成的同时运用自己的教学智慧，去促进更多的非预设生成，并及时捕捉住非预设生成的智慧火花，让课堂绽放生命的活力。

2.预设的主体是教师，而生成的主体是学生。生成是建构与生长，是师生与具体的教育情境发生交互作用，是师生、生生之间的交往和对话中出现的超出教师预设之外的新情况、新问题。这是一种能促进学生和教师共享教学的愉悦，不但有高质量的思维交锋和智慧启迪，而且有积极的情感体验。

二、学习中的“非预设生成”原因

1.是备课不充分吗？这些“学习生成”为什么是“非预设的”？是因为教师在教学设计的时候对学生了解不足，备课不充分吗？如果是这样，则要求教师在今后的备课过程中，提高对学生的研究，使教学设计更吻合于学生认知能力，并实现与学习材料的最佳结合。

2.以何种形式呈现？如何使“非预设生成”的学习成果成为激励师生提高学习互动质量的催化剂？“非预设生成”有时以行为的方式表达，有时以问题的方式呈现，有时以结果的方式存在。不论哪一种方式，“非预设生成”都会给师生带来意外的感觉。这种意外往往给学生带来探究的冲动，如果探究活动带来收获，学生就会有积极的情绪体现。

3.如何看待生成性资源？如果没有课堂生成，学生的主体性将无法体现，学生的数学探究活动就不是真实的，从而无法让课堂焕发出生命的活力。但是生成并非都是事先可预设的，非预设性生成信息也是一种资源，它和各种预设性的生成资源共同构成精彩的课堂。因此，在教学中面对各种非预设性生成信息时，要以积极的态度与科学的策略真诚应对。

三、教师该如何应对学生的非预设生成

1.非预设生成的主体是学生。动态生成的课堂体现出学生在学习中的主体地位，确立了教为学服务的意识。教师要根据学生在课堂上已经发生的变化情况，及时调整预设的方案，以适应学生的学习需求，促进生成。两个案例中学生的解答与教师的预设不一致，甚至产生了不同的方法，教师临时调整预设，顺应学生的想法，同时自己也在师生互动中产生了新的念头，有效地促进了师生互动生成。在生成中让学生的个性得到舒展和张扬，让师生创造性灵感得到淋漓尽致的发挥，让课堂充满创造的生机与活力。案例二中同样由于教师的包容与民主，让学生产生了不同的想法，这其中就包含了教师意料外的“非预设性生成”。对此，教师要善于倾听，用心去发现学生发言的闪光点，追溯思维的起因，并用一种开放的心态，充分利用学生的问题资源，在提炼成有效资源后，带着学生一起去分析，一起去讨论，一起去分享，使课堂再产生新的思维碰撞和思维交锋，从而再有所发现，有所拓展，有所创新，促进教学的不断生成和发展。

2.非预设生成中教师必须有自己的“价值判断”。教师面对意外要迅速反思：“这个想法是否更有价值？”“顺着这个思考将会有什么样的情况出现？”等等，及时对这些“意外”迅速过滤，从中出现可使教学进一步引向深入、拓展延伸的新契机。如案例一中，教师的预设与学生的生成完全不一致，但实际是由于解题思考的角度不同而出现了不同的答案，其实这两个答案是一致的，这就需要有教师的价值判断。这样的生成是有价值的，教师对预设的调整和生成的价值判断是正确到位的，这样的生成是有意义的。案例二中学生的回答虽是“答非所问”，但教师在顺应学生的同时，已巧妙地将其嫁接到正确的轨道上来了。

3.面对非预设生成，教师在顺应学生的同时必须有自己的“价值引领”。新课程倡导生成，并不是片面追求生成，不是漫无目地脱离数学文本的生成，更不是一种什么都对的“舍本逐末”式的生成。即时生成东西并不是都有价值，毫无价值的胡乱生成容易信马由缰，数学教学目标的达成往往会大打折扣。因此在顺应学生的生成时，教师要有所选择，要有适时、适度的“价值引领”，对那些无关的、意义不大的、没有多大价值的生成可以一笔带过，对那些有探究价值的生成，可以引导学生深入探究。案例一和案例二中的教师抓住学生的非预设生成，索性顺水推舟，把问题抛给学生，让学生有充分思考的时间（留白），从而产生新旧知识的“超链接”，获得了精彩的有价值的生成。

总之，在实施教学方案时，教师应及时捕捉课堂上的动态生成性资源，要敢于因势利导、打破计划，要经常对预定的目标、内容进行反思和调整， 促进学生的发展。