降雨量等值面生成方法的研究

陈 洁， 任 斌， 吴 可

（1.辽宁石油化工大学 辽宁 抚顺 113001；2.中兴通信股份有限公司 广东 深圳 518055）

等值面是空间中的一个曲面，在该曲面上的值等于某一个给定值。等值面不同于等值线，等值线是所有的属性值相同的点连成的线，等值面则是所有属性值相同的点合成的面、一个区域，在该区域内所有值都是相同的[1]。降雨量等值面可以清晰地反映地域内的降雨分布情况，是降雨分布的直观反映，对于及时分析流域降雨形势、洪水的预测和下游防洪有着重要的意义。

1 降雨量等值面生成方法

降雨量等值面的生成是根据已测点的数据来预测未知点的数据，利用已测点数据进行空间数据内插，以得到未知点数据。利用常规方法无法对空间中所有的点进行观测，但是可以获得一定数量的空间样本，这些样本反映了空间分布的部分特征，并可以据此预测位置地理空间的特征。空间数据内插法可以根据已知的空间数据估计预测位置空间的数据值。常用的空间数据内插方法有径向基函数法、反距离权重法和克里金方法。

1.1 反距离权重法

反距离权重（Inverse Distance Weighting，简称IDW）插值法是空间分析中的一种常用方法，被广泛的应用于各领域的插值计算中。反距离权重插值法认为各点的插值误差变化趋势各不相同，相互距离较近的事物要比相互距离较远的事物更相似，因此距离预测位置最近的测量值比距离预测位置远的测量值的影响更大。即距离预测位置较近的点分配的权重较大，权重随距离的增大而减小，因此称之为反距离权重。

1.2 径向基函数法

径向基函数（Radial Basis Function，简称 RBF），是某种沿径向对称的标量函数。假设，以为中心，到的径向距离为半径所形成的构成的函数系满足，称为径向基函数[2]。

径向基函数法是一系列精确插值法的组合，有薄板样条函数、张力样条函数、规则样条函数、高次曲面函数和反高次曲面函数等5种基函数。在不同的插值函数中，每种基函数都有不同的形状和结果。

1.3 克里金插值法

克里金（Kriging）插值法又称为空间自协方差最佳插值法，是一种求最优、线形、无偏的空间内插方法。在充分考虑观测对象之间的相互关系后，对每一个观测对象赋予一定的权重系数，加权平均得到估计值。克里金插值法类型分常规克里金插值和块克里金插值，最常用的克里金插值法为普通克里金插值算法[3-4]。

2 插值方法对比

2.1 等值面及均方根值

反距离加权插值法的公式较简单，特别适用于结点散乱，不是网格点的问题。由于这种插值是各节点上值的加权平均，它只能在节点上取到函数的最大值和最小值。作为精确插值器，径向基函数法不同于全局和局部多项式插值器，它们都是非精确插值器，即不要求表面穿过测量点。比较RBF和IDW插值器来看，IDW从不预测大于最大测量值或小于最小测量值的值，RBF用于根据大量数据点生成平滑表面。这些函数可为平缓变化的表面（如高程）生成很好的结果。对于反高次曲面外的所有方法，参数值越高，地图越平滑，对于反高次曲面则正相反。

以四川省崇州市山洪预警非工程措施项目中的23个雨量站的雨量数据为基础，时间从2011年8月19日早上8时至2011年8月20日早上8时，通过ArcGIS软件中的3种插值工具进行比较，对比数据如表1所示。

根据对比数据可得到3种插值方法降雨量等值面图，利用反距离权重加权法所生成的降雨量等值面图，当相邻监测点数据差别较大时，易出现“牛眼”现象，不能很好的反映降雨量真实曲面。利用径向基函数插值法所生成出的降雨量等值面图也具有“牛眼”现象，且“牛眼”范围更小，更不能反映真实曲面。利用普通克里金插值法插值出的等值面图能较好的反映降雨趋势，并考虑了数据的空间相关性，生成较为真实的曲面[5]。

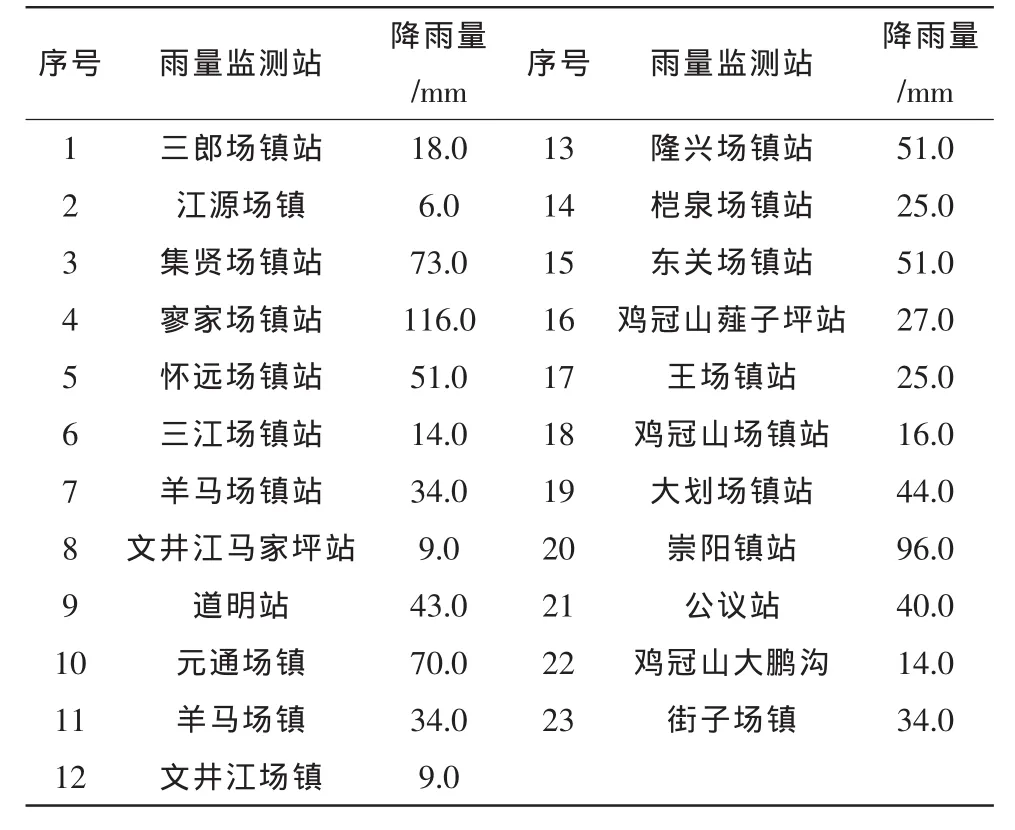
表1 观测站降雨量数据Tab.1 Rainfall data of observation

交叉验证比较图如图1所示，从图中可以看出，用克里金插值法方法所得出的均方根比IDW和RBF方法得出的均方根都小，对于空间插值，均方根越小，插值效果越好[6]。

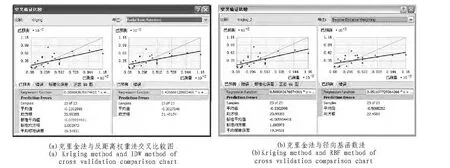
图1 交叉验证比较图Fig.1 Comparison chart of cross validation

根据等值面曲面和预测误差对比，我们将选择普通克里金法作为本次降雨量等值面绘制的空间插值方法。

2.2 参数的优化

克里金插值方法最优的条件为：1）均方根最小；2）标准平均值最接近0；3）标准均方根最接近1；4）平均标准误差最接近均方根。通过对参数进行设置，得出最优克里金插值参数[7-8]。

对于参数优化，将利用ArcMap中的地理统计向导来完成，以获得最优克里金参数。在表2和表3中将列出对比参数组中的一部分对比参数。

从数据对比中可以看到，第7组数据最符合克里金插值最优条件，参数为步长：0.021113；范围：0.1690599；偏基台：815.2132；块金：0。

3 结束语

在研究降雨量等值面生成方法基础上，对三种方法进行比较，用克里金插值方法得到的均方根值较小，生成的等值面较为真实。对于各种空间数据插值方法而言，没有绝对最优的空间插值方法，只有在特定的条件下的最有效方法。因此，必须依据空间数据的内在特征，经过反复实验，选择最优的空间数据插值方法。

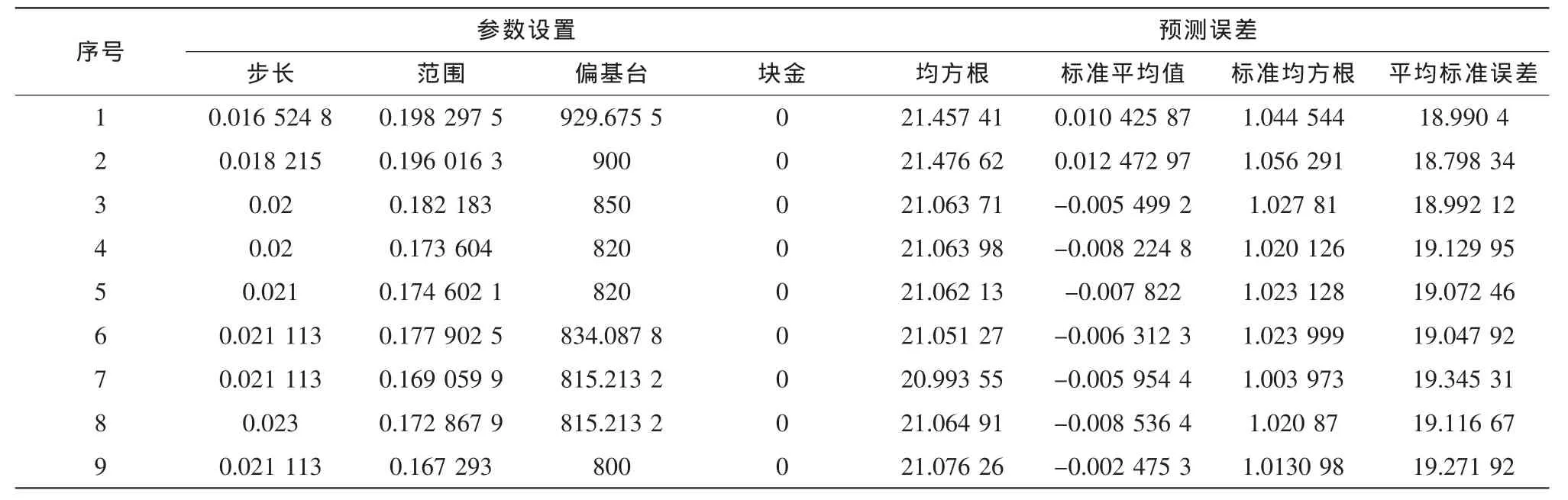
表2 参数设置与预测误差Tab.2 Parameter Settings and the prediction error

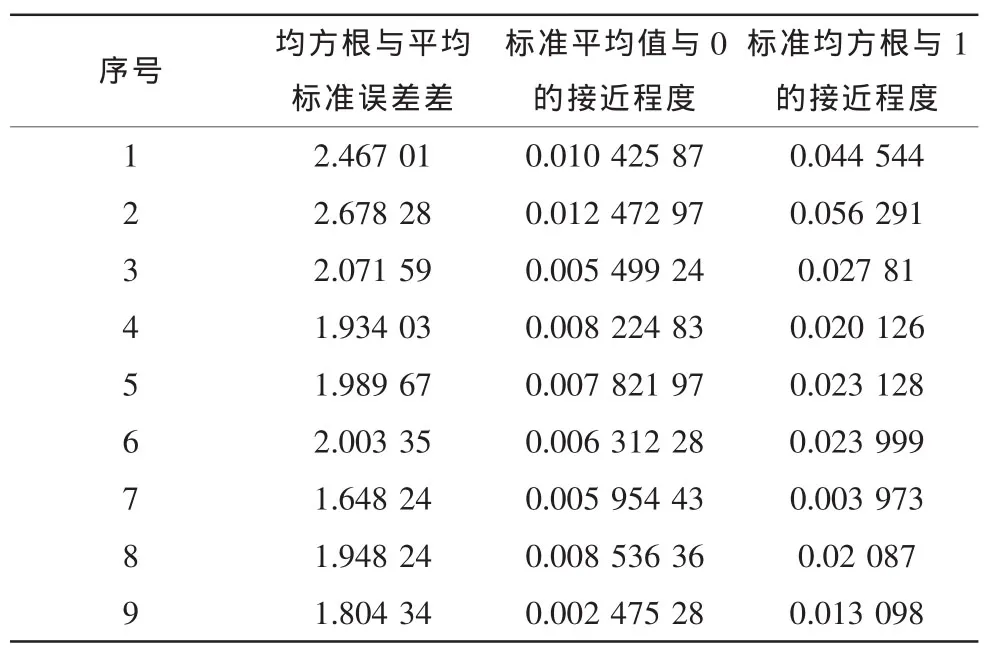
表3 参数对比表Tab.3 Parameter comparison table

[1]百度知道.等值面与等值线的区别[EB/OL]（2011-07-25）.http://zhidao.baidu.com/question/297314471.html.

[2]张宏，温永宁，刘爱利，等.地理信息系统算法基础[M].北京:科学出版社，2006.

[3]Philip G M，Watson D F.A precise method for determining contoured surfaces [J].Australian Petroleum Exploration Association Journal，1982（22）:205-212.

[4]Watson D F，Philip G M.A refinement of inverse distance weighted interpolation[J].Geoprocessing，1985（2）:315-327.

[5]宋丽琼，田原，邬伦，等.日降水量的空间插值方法与应用对比分析[J].地球信息与科学，2008，10（5）:566-572.SONG Li-qiong，TIAN Yuan，WU Lun，et al.Daily precipitation spatial interpolation method and application of comparative analysis[J].Information and Earth Cience，2008，10（5）:566-572.

[6]白江涛.基于GIS的关中-陕南地区降雨量空间插值分析[J].安徽农业科学，2012，39（33）:20872-20876.BAI Jiang-tao.In southern shaanxi rainfall in the guanzhongbased on GIS spatial interpolation analysis[J].Journal of Anhui Agricultural Sciences，2012，39（33）:20872-20876.

[7]郜邦勋，武江林.基于GIS环境的降雨量等值线（面）分析方法[J].贵州气象，2004，28（5）:30-33.GAO Bang-xun，WU Jiang-lin.Rainfall isoline based on GIS environment（surface）analysis method[J].Journal of Guizhou，2004，28（5）:30-33.

[8]汤国安，杨昕.ArcGIS地理信息系统空间分析实验教程[M].北京:科学出版社，2006.