基于高调制频率的快速数字锁相算法
2015-06-08蒋国亮
蒋国亮,杨 晖,李 然
( 上海理工大学光学与电子信息工程学院,上海 200093)
基于高调制频率的快速数字锁相算法
蒋国亮,杨 晖,李 然
( 上海理工大学光学与电子信息工程学院,上海 200093)
为了提高数字锁相的检测速度以及其最高调制频率,改善数字锁相放大的实时检测性能,文中提出了一种新型快速数字锁相算法。文中根据方波参考信号傅里叶展开存在奇次谐波,使得调制频率等于参考信号频率的2m-1倍。同时,通过将采样频率设为调制频率的4的整数倍,保证两路参考信号的正交性。在相敏检波算法实现中,仅仅存在加减法运算,消除了乘法运算,提高了数字锁相算法的运算速度。而且,基于普通微处理器的数字锁相放大能达到的最高调制频率也得到了有效的提升,改善了锁相放大的实时性能。实验表明,该算法既具备较高的速度,又能提高锁相放大的实时性,使得数字锁相对微弱信号的实时检测在普通微处理器上的实现成为可能。
数字锁相算法;调制频率;微弱信号;相关运算;奇次谐波;方波参考
0 引言
微弱信号检测技术广泛地应用在光谱学、光通讯、天文、声纳、雷达以及生物医学工程,用以检测这些领域中被噪声背景所淹没的微弱信号。而基于相关检测原理的锁相放大器(lock-in amplifier,LIA)这一微弱信号检测仪器是目前准确度较高,应用最广泛的装置[1-4]。早期的锁相放大器都是由模拟电路来实现的,但传统的模拟LIA存在温度漂移和其他非线性的低频特性的影响。随着数字技术的不断发展,数字锁定放大器(DLIA)逐步取代了模拟LIA。DLIA采用了数字乘法器和数字滤波器在动态范围、噪声方面远优于模拟器件,大大提高了锁相放大测量的准确度。
国内外众多科研人员将数字锁相检测应用到各自领域,并对提高数字锁相检测的性能做了大量的研究[5-10]。天津大学的李刚教授,提出了使用过采样技术简化外围电路和减少量化噪声[8]。同时,为了提高DLIA的算法速度,把采样频率设为调制频率的4的整数倍,基本去除了锁相放大算法中的乘法运算并减少了大量的减法运算,降低了运算量和存储量,极大地提高了数字锁相算法的速度[10]。Masciotti等人通过使用矩阵乘法,极大地减少了多调制频率数字锁相算法的运算量[10]。上述研究极大地提高了数字锁相算法的速度,然而,在一些对调制频率有很高要求的在线实时系统上,传统的数字锁相算法无法同时满足系统的高调制频率和实时性。
本文针对上述问题,提出了一种基于方波参考信号的快速数字锁相算法。首先,把调制频率设为方波参考频率的2m-1倍,然后再将输入信号与参考信号相乘。由于方波的傅里叶级数包含有奇次谐波,上述信号相乘的结果一定会产生一个含有输入信号幅值和相位信息的直流分量。在相同的时钟消耗下,该算法大大提高了数字锁相放大的最高调制频率,也提高了数字锁相系统检测的实时性。此外,该数字锁相算法只有加减法运算,几乎消除了所有的乘法运算,进一步提高了运算速度并克服了算法实现对处理器的依赖性。
1 数字锁相原理
相关检测是应用信号周期性和噪声随机性的特点,通过自相关或互相关运算,达到去除噪声、检测信号的一种技术。锁相放大器就是采用互相关技术,通过对待测信号与参考信号的互相关运算,实现对待测信号中有效信号的提取,达到提高信噪比的目的。传统的正交数字锁相放大器采用了双相关器的原理,参考信号由两路相互正交的方波信号构成,其原理框图如图1所示。
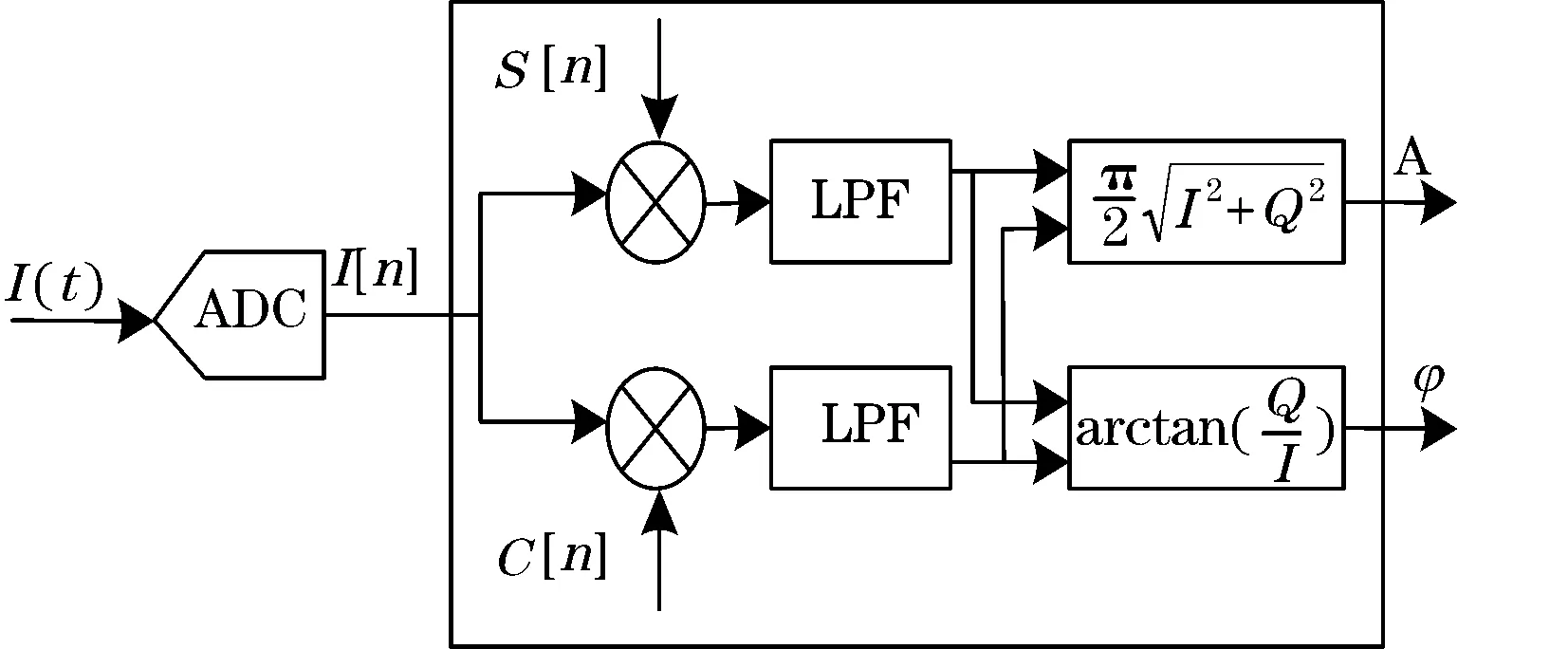
图1 正交锁相放大器原理框图
假设输入信号为
I(t)=Asin(2πf0t+φ)
式中:A为幅值;φ为相位。
以采样频率fs=Nfm对输入信号进行采样,N≥2,得信号序列为
I[n]=Asin(2πn/N+φ),n=0,1,2,……,M-1
(1)
式中M为总采样点。
参考信号为与输入信号频率相同的方波,且参考信号不用进行采样,可由微处理器根据N来产生正交参考序列S[n]和C[n]。
(2)
(3)
输入信号分别与正交参考序列相乘实现相敏检波的功能,得到的相关信号中的直流分量仅与原始信号的幅值和初相位有关,因此通过数字低通滤波器取出直流分量即可得到输入信号的幅值和相位信息。通常采用的低通滤波器为平均滤波器[11],信号的正交相关运算和滤波过程如下:
(4)
(5)
式中M为整周期采样点数,同时也对应着低通滤波器的时间常数。
输出的2个分量一个是与cos(φ)成正比的同相分量,一个是与sin(φ)成正比的正交分量,将2个信号经如下运算即可得到有用信号的幅度和相位:
(6)
(7)
2 高调制频率快速锁相算法
2.1 算法原理
传统的锁相放大器要求调制频率与参考频率一致才能正常工作,而本文提出的锁相放大器的调制频率fm为方波参考频率fr的2m-1倍。由于方波的傅里叶展开式中包含有奇次谐波的高频成分,因此当调制信号频率为参考信号的奇次倍时,其相关运算结果仍然能产生一个直流分量仅与原始信号的幅值和初相位有关。此时,输入信号的正交相关运算和滤波过程如下:
(8)
(9)
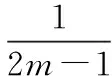
(10)
(11)
2.2 算法实现
高调制频率快速锁相放大器中,调制频率是参考信号的2m-1倍,即采样1个完整的计算周期M个采样点,应有2m-1个周期输入信号序列而参考信号仅为1个周期序列。因此,在一个完整的计算周期内,由处理器产生的正交参考序列S[n]和C[n]分别为
(12)
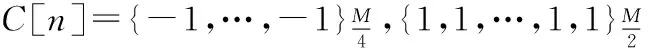
(13)
此时,相关运算的结果为:
(14)
(15)
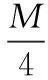
图2(a) 是该算法的相敏检波原理图,图中调制频率为参考信号频率的5倍,图2(b)为传统锁相放大相敏检波原理图。图2(a)和图2(b)的采样频率都设为参考频率的20倍,且参考信号与输入信号相位差为0。
从式(14)和式(15)可以看出,在正交互相关计算中的乘法运算全部消除,仅仅通过加减法运算就能够实现互相关运算,大大降低了计算量。对于相同采样频率的传统数字锁相算法,若采样M个点,正交互相关运算中乘法运算次数为 2M,加法运算次数为2(M-1);而高调制频率快速锁相算法中乘法运算次数为0,加减法次数为2(M-1)。显然,随着采样周期的增加,高调制频率快速锁相算法的优越性能越能体现。同时,由于参考信号的频率低于调制频率,减少了序列产生占用的时钟周期,进一步减少了对处理器的时钟消耗。
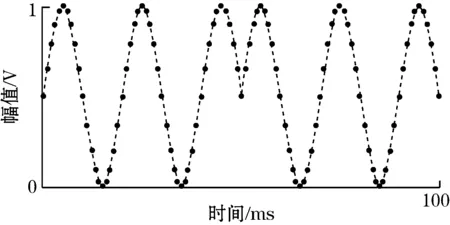
(a)高调制频率数字锁相m=3
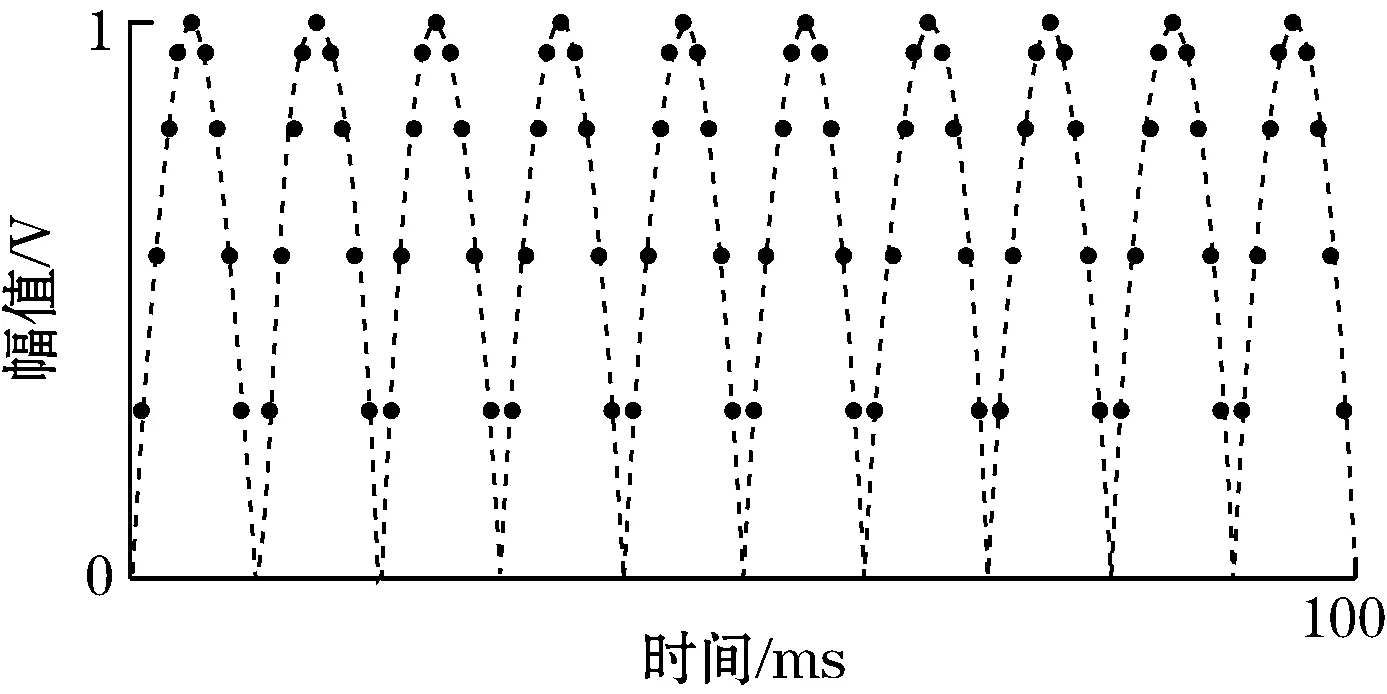
(b)传统数字锁相图2 相敏检波原理图
3 实验和仿真
为了验证这种高调制频率快速数字锁相算法的有效性,利用LABVIEW进行仿真,通过改变幅值和调制频率与参考信号频率的倍数,比较真实值和计算出的幅值和相位。
验证计算幅值的有效性:通过仿真,产生一系列的频率为方波参考信号奇次倍的正弦调制信号,初相位和直流分量为0,采样频率设置为调制频率的20倍。改变调制信号的幅值,并加入白噪声作为输入信号,采用该方法计算的幅值如表1所示(保留小数点后5位)。
表1 不同调制频率下幅值测试结果V
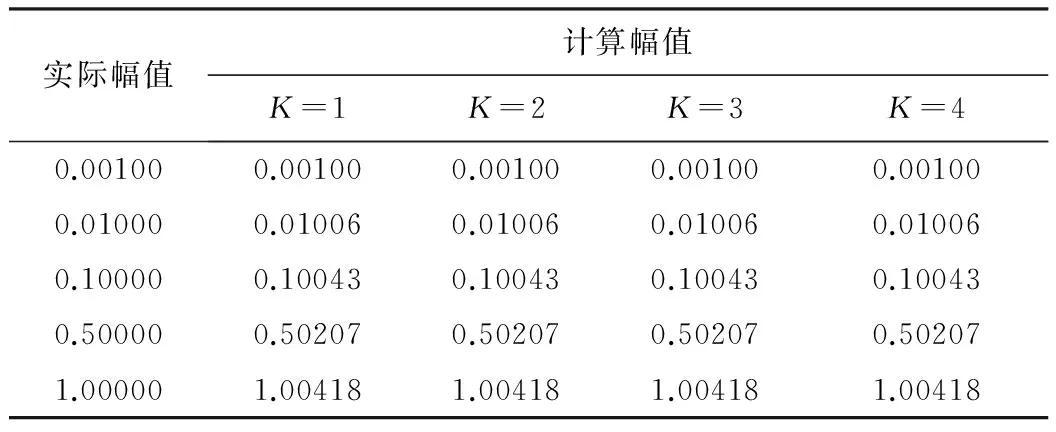
实际幅值计算幅值K=1K=2K=3K=40.001000.001000.001000.001000.001000.010000.010060.010060.010060.010060.100000.100430.100430.100430.100430.500000.502070.502070.502070.502071.000001.004181.004181.004181.00418
验证计算相位的有效性: 通过仿真,产生一系列的频率为方波参考信号奇次倍的正弦调制信号,其中幅值为1 V,直流分量为0,采样频率设置为调制频率的20倍。改变调制信号的初相位,并加入白噪声作为输入信号,采用该方法计算的相位如表2所示(保留小数点后5位)。
表2 不同调制频率下相位测试结果rad
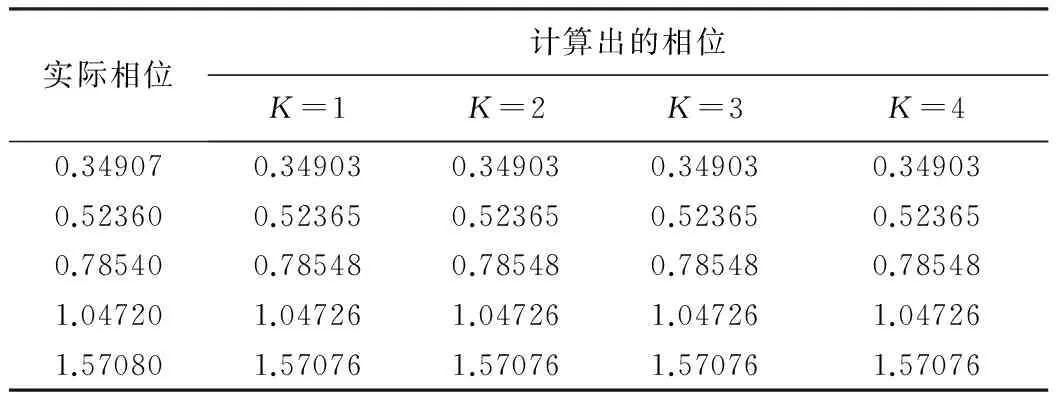
实际相位计算出的相位K=1K=2K=3K=40.349070.349030.349030.349030.349030.523600.523650.523650.523650.523650.785400.785480.785480.785480.785481.047201.047261.047261.047261.047261.570801.570761.570761.570761.57076
在表1和表2中,K=1的情况下可认为是传统锁相放大的测量值。由表1可以看出,采用这种高调制频率的快速锁相放大算法测得的幅值与传统锁相放大算法相一致不会引入误差,且测得的准确率大于99.5%。而,由表2可看出,这种高调制频率的锁相放大算法测得的相位与传统的锁相放大算法完全一致。
4 结束语
本文研究了数字锁相放大器对微弱信号检测的相关理论,推导了参考信号为方波时的相关运算结果,利用了方波傅里叶级数展开包含的奇次谐波高频成分,提出了使用调制频率为参考信号频率的奇次倍来实现相敏检波运算,而非传统的调制频率必须等于参考频率。本文提出的高调制频率快速数字锁相放大算法,与传统的数字锁相放大相比,去除了几乎所有有的乘法运算,同时通过使用相对较低的参考频率减小了处理器的负荷。实验仿真结果表明,这种新型的数字锁相放大算法并没有任何的理论误差。同时,该算法还极大地提高了运算速度,提高了实时锁相放大检测的最高调制频率,使得基于数字锁相放大的微弱信号处理可以在普通的微处理器上实现。
[1] ANDERSSON M,PERSSON L,SVENSSON T,et al.Flexible lock-in detection system based on synchronized computer plug-in boards applied in sensitive gas spectroscopy.Rev.Sci.Instrum,2007,78(11): 113107-113113.
[2] RIPKA P,DRAXLER K,STYBLIKOVA R.Measurement of DC Currents in the Power Grid by Current Transformer.IEEE Trans.Magn,2013,49(1): 73-76.
[3] BENGTSSON L E.A microcontroller-based lock-in amplifier for sub-milliohm resistance measurements.Rev.Sci.Instrum,2012,83(7): 075103-075110.
[4] HSDPSR J,CHEN S F,GORDILLO A,et al.Digital lock in amplifier: study,design and development with a digital signal processor.Microprocessors and microsystems,2004,28(4): 157-162.
[5] BARRAGAN L A,ARTIGAS J I,ALONSO.A modular,low-cost,digital signal processor-based lock-in card for measuring optical attenuation.Rev.Sci.Instrum,2001,72(1): 247-251.
[6] SONNAILLON M,BONETTO F J.Lock-in amplifier error prediction and correction in frequency sweep measurements.Rev.Sci.Instrum,2007,78(1): 014701.
[7] 李刚,张丽君,林凌. 一种新型数字锁相放大器的设计及其优化算法.天津大学学报,2008,41( 4): 429-432.
[8] SONNAILLON M O,BONETTO F J.A low-cost,high-performance,digital signal processor-based lock-in amplifier capable of measuring multiple frequency sweeps simultaneously.Rev.Sci.Instrum,2005,76(2):024703.
[9] 李刚,周梅,何峰,等.基于数字锁相相关计算结构的优化算法.电子与信息学报,2012,34(3): 744-748.
[10] MASCIOTTI J M,LASKER J M,HIELSCHER A H.Digital Lock-In Detection for Discriminating Multiple Modulation Frequencies With High Accuracy and Computational Efficiency.IEEE Trans.Instrum.Meas,2008,57(1): 182-189.
High Speed Digital Lock-in Algorithm Based on High-modulate Frequency
JIANG Guo-liang,YANG Hui,LI Ran
(School of Optical-Electronical and Computer Engineering,University of Shanghai for Science & Technology,Shanghai 200093,China)
In order to improve the speed and the maximum modulation frequency of the digital lock-in,a high speed digital phase-locked algorithm was presented in this paper.In this paper,a new algorithm that make the modulate frequency equal to 2m-1 of square reference frequency was proposed to implement a lock-in,which was based on odd harmonic components in the square wave reference.The sampling frequency was four times as large as the modulate frequency to insure the reference sequences orthogonal.In the implementation of phase sensitive detection,only additions and subtractions were used,which speed up the computation in lock-in.Furthermore,the maximum modulate frequency of a lock-in was enhanced considerably with a general microprocessor.The results of the experiments show that the new algorithm not only has high speed,but also improves the performance of real-time detection,which makes it possible for a general microprocessor to implement weak signal detection by the new algorithm in real time.
digital lock-in algorithm;modulation frequency;weak signal;correlation operation;the odd harmonic;square wave reference
国家自然科学基金(61007002);上海市教育委员会科研创新项目(15ZZ072)
2015-03-16 收修改稿日期:2015-07-02
TP206
A
1002-1841(2015)12-0126-03
蒋国亮(1992—),硕士研究生,研究方向为信号与信息处理。E-mail:jdangg192@163.com
