声波时差法计算地层剥蚀量问题的斧正

刘玉瑞

(中国石化江苏油田分公司科技处，江苏 扬州 225009)

自Magara声波时差法计算地层剥蚀厚度(Hb)和真柄钦次用该法恢复Hb发表后［1－2］，因其原理简单、参数易取，成常用方法，并不断对其提出改进［3－5］。上世纪，探索在苏北盆地应用未成功，原因是不满足使用条件。新世纪，又有人用该法计算多个层位 Hb［6－11］①，②。分析表明，这些成果无一例正确;搜索中文期刊网，发现此类论文问题多多［12－23］。这些错误数据和认识，不断被反复引用，以至泛滥成灾。因此，有必要加以斧正。

1 声波时差法计算剥蚀量回顾

下面简介Magara法基本原理及国内较有影响的牟中海、周瑶琪对原模型的扩展观点。

1.1 Magara声波时差法

为便于问题讨论，将Magara法原理简介如下。该法建立在Athy(1930)孔隙度( )与深度(H)关系( =0e－CH)及 Wyllie(1958)的 与声波时差(△t)关系{ =(△t－△tma)/(△tw－△tma)}的理论基础上，推导出△t－H关系式:

其中，△t—深度H处页岩的声波时差，μs/m;△t0—外推至地表的声波时差，μs/m;H—页岩埋深，m;C—正常压实趋势斜率的常数，m－1。

正常压实情况下，页岩△t－H关系呈指数变化。在连续地层段，相关曲线是连续变化的;当地层抬升剥蚀和再埋藏后，曲线可能会偏离原变化趋势，由此可计算 Hb和地层最大埋深(图 1)［1－2］。

图1 经典的声波时差法恢复剥蚀量示意图

使用条件判别:⑴满足Hb＞Hx(新沉积地层厚度)前提。真柄指出［2］，当 Hb＜Hx时，剥蚀前页岩压实作用的标记会被新沉积物作用消除，则该法不适用。⑵页岩必须是正常压实，欠压实不适用。⑶Hb太小、断层和裂缝发育等情况，该法慎用。

应用关键:获取△t0和制作正常压实趋势线。如图1所示，得到△t0值有两种途径。

(1)借用理论的△t0值。Magara 和真柄［1－2］均推荐△t0=200μs/ft(656μs/m)，对应的终止点 =62%;依据是当粘土含量达到总容积体积的38%之前，声波传播时间几乎保持不变;其后，传播时间随粘土含量增加而缩短。据此，国内常用650～620 μs/m理论值。把正常压实趋势上延与△t0垂线相交即为古地表，交点到剥蚀面垂距为Hb值。

(2)实际资料求△t0值。研究区尽可能多选井，制作剥蚀面上覆新地层的正常压实趋势，然后将这些趋势外推到现在地表，取得多个△t0值，选最大值的最接近无剥蚀△t0值;再把老地层正常压实趋势上延与△t0垂线相交，定古地面和求Hb值。

1.2 牟—周的扩展观点

牟中海、周瑶琪等认为［4－5］，判断声波时差法是否适合计算Hb的标准，不应依据Hb与Hx的大小比较，只要上覆Hx产生的压力(Px)小于Hb在相同深度点的压力(Pb)，未改造老地层的压实效应，该法就适用。

1.2.1 牟的扩展［4］

按新地层、老地层的压实趋势斜率关系(C新、C老)，分7种情况:①C新位于C老右边(图2a－c)，表示对老地层施压Pb＞Px，适用Magara法;②C新=C老并在同一线上(图2d)，说明Hb与Hx在相同深度点压力相同，老地层被改造，不适用Magara法;③C新≥C老并位其左边(图2e－f)，反映老地层欠压实及Pb≤Px，不适用Magara法;④C新＜C老并位其左边(图2g)，认为对老地层施压 Pb＞Px，即便 Hb＜Hx，只要新沉积物粒度细、地压梯度就小，剥蚀地层粒度粗、地压梯度就大，即不破坏老地层的压实规律，适用Magara法。

图2 扩展的声波时差法恢复剥蚀量示意图［据牟中海(2000)、周瑶琪(2000)合并略修改］

1.2.2 周的扩展［5］

将页岩△t－H压实趋势按图2中Ⅰ～Ⅵ型分6种模式，Ⅰ、Ⅳ、Ⅵ型含义与牟的相近;Ⅱ、Ⅲ和Ⅴ型内涵不同，认为都适用Magara法。理论是:孔隙度不只是埋深的函数，沉积速率、沉积环境和构造背景都对压实效应也有重要影响，这是C新、C老斜率经常不一致的原因;而不整合面上、下附近的致密层或高渗透层异常压实，正好阻挡了新地层对下伏老地层压实效应的影响。

牟、周分别在柴北缘和东营凹陷应用，论著发表后，广被引用，认为是对经典法的扩展。

2 问题辨析与斧正

剥蚀量恢复是盆地分析重要内容，人们一直在探索求取剥蚀量的各种途径。Magara法以简易受欢迎，改进建模和试图拓宽使用范围一直不停。本文认为，就牟—周法的扩展而言，论据不足，缺乏可操作性，并易诱导生错。

2.1 牟—周扩展的理论缺陷与斧正

牟—周的理论是改遵循Hb＞Hx使用条件，为遵循Pb＞Px原则，即未改造老地层的压实效应。无疑，这是对经典理论的完善。但牟—周并未遵循该原则;相反，都突破了这一原则，导致方法和实例都错。

2.1.1 牟—周的论文数据都突破了Pb＞Px原则

众所周知，地下某处的上覆静岩压力可表示为:

其中，P—上覆岩层压力，MPa; —岩石平均孔隙度，%;ρf—岩石孔隙流体的平均密度，kg/cm3;ρa—上覆岩石基质的平均密度，kg/cm3;H—地层垂直深度，m;g—重力加速度，m/s2。

那么，要达到Hb＜Hx和Pb＞Px情况，需满足:

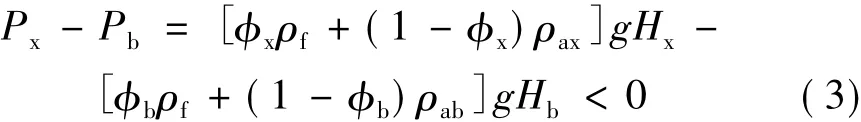
即，(ΦxHx－ ΦbHb)ρfg+ ［(1 － Φx)ρaxgHx－(1 － Φb)ρabgHb］ ＜ 0

因，(ΦxHx－ ΦbHb)ρfg ＞ 0

若Hb与Hx的岩性密度、厚度、孔隙度相近，则无法满足上述条件。为此，牟文提出假想［4］:若新沉积地层为细粒泥岩，被剥蚀地层为砂岩或砂砾岩，那么泥＞砂、ρa泥＜ρa砂，则有 Pb－Px＞0。

实际上，牟文并未用上述公式推演，而是揣测;由此铸就其理论推导的错误，斧正如下。

首先，考察砂岩、页岩 －H变化。沉积学原理表明，岩性和埋藏压实是影响岩石物性和密度的两大主因;原始沉积物泥＞砂、ρa泥＜ ρa砂，埋深压实都是 递减、ρa渐增，在表浅层，泥降低和ρa泥增大明显高于砂和ρa砂的变化速率。据页岩、砂岩 －H 关系(图 3)［2、24］，结合苏北盆地数据(图 4)，可知:约在100～340 m埋深区间(最大670 m左右)，出现页岩与砂岩的 交汇点，继续埋深变为泥＜砂、ρa泥＞ ρa砂情况，这种关系一直维持到 →0，ρa→岩石骨架最大密度。由此可见，牟文的假想，仅仅存在于表浅层狭小的地质窗口。

图3 砂岩、页岩的 －H 关系(引自［2、24］)

图4 XuQ1井砂岩、泥岩的ρ－H关系

其次，定量考察窗口大小与可操作性。假设:Hb=340 m砂岩，参考图3取小值砂=35%，参考图4取大值ρa砂=2.1 g/cm3;Hx泥岩取较大值泥=50%，取较小值 ρa泥=2.0 g/cm3，用公式⑸计算，当Hx/Hb＜1.365时，即 Hx＜460 m，有出现 Pb＞Px可能。

这是假定公式⑷为零时的极端测算。实际上，随着Hx与Hb差值增大，厚度差引起的流体压力差值增大，远远抵消了新地层与剥蚀地层之间很小的密度差、物性差可能引起的压力差值，即Hx/Hb比值远比上述测算的小。这个差值还抵不上△t0选理论值区间600～656 μs/m的剥蚀量150～200 m误差区间。

可见，出现Hb＜Hx、Pb＞Px的地质窗口极小或不存在，准确判别更不可能，无实际应用意义。

整理牟、周论文数据可知 (表 1)［4－5］，除G14井Hb＞Hx、Pb＞Px剥蚀量可信外，其它井都是Hb＜Hx、Pb＜＜Px情况，显然不适用 Magara法。用周文的方程，本文算出其新地层△t0新，发现4个△t0新≥678 μs/m，超 656 μs/m 理论上限;5个△t0老在938～2 163 μs/m间，都说明不适合用Magara模型。由此证明，牟、周二文中，但凡Hb＜Hx情况，必有Pb＞Px，其剥蚀量数据和方法都是错误的。

表1 牟—周文的扩展声波时差法剥蚀量数据表

2.1.2 牟文的假设完全脱离地质常识

牟文假定［4］，厚4 000 m的粗粒沉积平均密度2.7 g/cm3产生的压力，相当于厚5 143 m(注:原文笔误为15143 m)细粒沉积平均密度2.1 g/cm3产生的压力，由此推断后者厚度大于前者1 000 m以上，也适用Magara法。

可以肯定，这种假设犯了地质常识和逻辑错误。一是2.7 g/cm3近乎碎屑岩的最大骨架密度，如此高密度岩石，埋深至少3 500 m以上;若剥蚀的是此类岩石，得先剥掉上覆密度小于该值的巨厚地层，那么剥蚀总幅度至少7 500 m。因为，剥蚀发生在沉积停止后，从低密度表层沉积物开始，而不是从深处高密度岩石起始。所以，牟的假设不符合地质常识和逻辑;二是5 000 m厚的泥岩平均密度该在2.6 g/cm3左右，绝不止2.1 g/cm3，这也是地质常识。由前面已知，泥岩密度随埋深快速递增，在埋深670 m左右全面超过砂岩密度，砾岩情况要复杂些(如图3、图4所示)。可见，牟文的假设多么荒谬，完全错误。

2.1.3 牟、周二文选用判别Magara法可用性的准则不科学

牟文提出判别Magara法可用性的新准则是，依据新、老页岩压实趋势斜率C新与C老的大小、左右位置及一致性关系的7种情况，来判别新地层、剥蚀地层对老地层的压实效应是否一致，以及是否适用Magara法。周文则用页岩△t－H压实模式定性识别，无定量方法，并且认为不整合附近的致密层可阻挡新地层对下伏老地层压实效应的影响。两文都显著扩大了Magara法使用范围，但无直接的可定量反映Pb、Px大小的方法。

显然，新的判别准则缺乏科学依据。首先，页岩压实趋势C值不是岩层压力大小的函数，不反映施加压力大小。C值大小反映页岩正常压实趋势变化的快慢，其大小与沉积速率、压实速度等因素有关，C值随埋藏或沉积速率降低而加大［2］。好比压力梯度不直接反映压力大小，压力还与施加厚度有关。其次，按牟文新准则，如图2C情况，C新＜C老且位其右边时，按理一直是Pb＞Px;但当△t0老＞△t0新时，就会有Hb＜Hx情景，出现Pb＜Px情况，且C老/C新比值越大，矛盾越严重，证明选C值作为判别准则是不合理的。其三，周文的定性判别法更不科学，无标准可循，也无法排除欠压实。

可见，Magara法原有的判别准则是正确的。

2.2 众论文的问题分析与斧正

阅览有关计算剥蚀量的论文，发现问题很多;苏北盆地此类报告无一例正确，分析如下。

2.2.1 不遵从Magara法原则，产生大量错误数据

一是论文和报告声称用Magara法，但不阐述任何理由，就突破Hb＞Hx准则，得到很多Hb＜Hx的剥蚀量数据(表 2)［7－10、14、18、19］②;二是阐明引用牟—周的扩展法，计算不同盆地剥蚀量，得到很多Hb＜Hx情况的成果［11、12、15、16、20］①。由前面论述很容易判断，这些数据都是在Pb＜Px下得到的，无一正确。

表2 部分论文的声波时差法剥蚀量数据表(单位/m)

2.2.2 模型、坐标系和方程式三者不匹配

Magara法方程是指数形式，在算术坐标系上压实趋势线呈一条曲线;若要得到直线压实趋势线，两种办法:一是选△t半对数坐标系，回归公式选对数方程式;二是对指数方程取对数，变换为线性方程，此时△t刻度为ln△t，回归公式应选线性方程式，即模型、坐标系和方程式三者必须一致。

但是，有不少论文和报告三者不一致，竟也能奇迹般地得出“正确”结论?一是用算术坐标系，居然能回归出直线来［7－10、17］①;二是用算术坐标系配对数方程式［9］;三是把△t－H指数式变换为线性式了，但线性方程回归错了［21－23］。因此，这些奇葩论文的剥蚀量数据都是不可信的。

2.2.3 随意用△t0理论值

获取可靠的老地层原始地表△t0值是恢复剥蚀量的关键环节，很多时候用实际资料不易得到;为此Magara和真柄推荐了理论值，但前提是遵守Hb＞Hx原则。如今，被演泽成任意不整合面深度和地质条件都可用的参数。但凡新地层无法得到△t0值，或者实际值有矛盾，不加分析都借用;如文献［19］选656 μs/m理论值，标杆图Zhang2井计算实际△t0=691 μs/m，超过理论界限速度;文献［20］用实际资料定△t0=600 μs/m，但与多数井不吻合，如G49井为645 μs/m，L4 井高达 689 μs/m。

目前，这种借用和两层皮现象很普遍。文献［4－23］，凡列出回归方程的，经计算验证，无一篇数据是完全合格的，仅个别井可信;造成了个个盆地、处处不整合面都可计算剥蚀量的“假象”。

2.2.4 伪原始资料问题

苏北盆地恢复剥蚀量的众论文和报告问题成灾。除上述共性问题外，文献［9］等有伪资料现象。一是肆意挪动井位。W8井位于高邮凹陷北斜坡西部韦庄地区，被作者挪到66 km之遥的东部吴堡断裂带，用于标定一条北北西—南南东向G78测线区域地震大剖面的剥蚀量，作为全盆恢复剥蚀量的标杆井。二是W8井竟然能提取出两套数据的△t－H关系来(图5a、b)。图 5a、b 引自文献［9］，测井曲线为本文添加。可以看出，除上部新地层数据与曲线稍吻合外，下部老地层两套数据都与测井不符，资料严重失实。三是用算术坐标系回归出直线来，方程却是对数形式，新地层△t0=671 μs/m，超理论上限。四是图5a深度刻度下半段正确，上半段全错。五是建湖隆起为三垛组物源区，被恢复出了大套地层;而且，平面图上W8剥蚀量比井上少约170～400 m。可见，该文是极不严肃的伪论文。

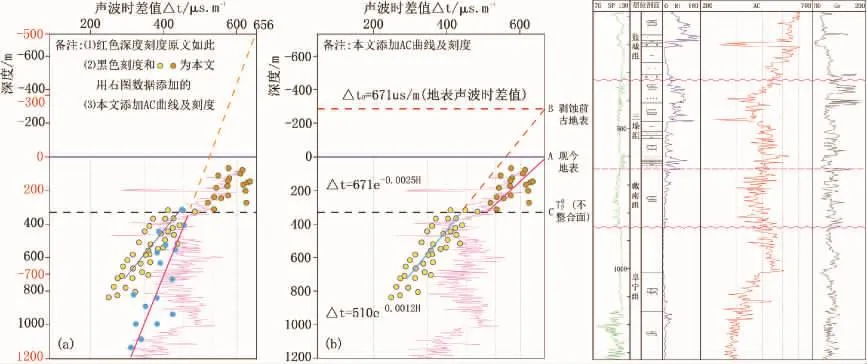
图5 W8井声波时差法剥蚀量恢复(据徐田武［9］，修改)

2.2.5 基础工作做得差

一是缺乏分析和交代地质情况。牟文明确提出Hb为粗粒物、Hx为细粒沉积时，才可能出现Hb＜Hx、Pb＞Px情况。这点纷纷被引用，但无人交代其研究对象是否属这种情况;像苏北盆地、渤海湾盆地的新近系/古近系不整合面，上覆均为粗的砂砾岩、下伏为细的砂泥岩，这种剖面不该用牟法，也做出了诸多自称“合理”的成果。另外，不分析剥蚀面之上新地层结构特征，也鲜有说明下覆老地层异常压实情况;不阐明地层剖面完整性、有无多个不整合面叠置，也不说明断层、裂缝和火成岩对声波时差的影响及取值情况等。

二是曲解原理，随意作图。对有多个不整合面的井恢复剥蚀量时，曲解原理，将多个不整合面拆开，分别作图恢复，以掩盖矛盾(图6)。图6a是用报告②M36井两张剥蚀量图拼的，图6b是报告①Xu15井两张图拼的，两图错误太多。文献［18］直接用声波曲线表示页岩压实情况，压实趋势C线竟然与声波曲线趋势成30°夹角。由此可见，这些文章结论绝不可信，还沦为科技笑话。

图6 上、下剥蚀量图拼合图(据报告①②编)

三是不做误差分析。缺少对声波曲线资料、页岩取值层、提取数据的可靠性与误差分析。对数据集是否满足计算精度欠分析;如图6中，数据集分散、相关性极差，完全不符合做剥蚀量计算。此外，计算结果是否符合地质情况分析的也少。

2.3 苏北盆地剥蚀量问题的讨论

十年 来 用 声 波 时 差 法［6－11］①②和 古 温 标法［6、10、11、25］，计算苏北盆地三垛组剥蚀量的论文和报告较多;这些文章互引、互证，都称计算数据合理。研究发现，这些结论无一可信，分析如下。

2.3.1 声波时差法不适合计算苏北盆地剥蚀量，恢复数据不可信

一是地质条件不满足Magara法。阜四—阜二段页岩全盆性欠压实，内坡—深凹戴南组页岩也见欠压实，断层多、剥蚀面多、火成岩多，新地层厚度超前期的剥蚀量;无实际的页岩△t0值，选不出符合Magara法的井，这是上世纪探索无果的主因。二是以上各文都不遵守Magara法原则。不交代剖面和取资料信息，许多剥蚀量是在Hb＜Hx下求得的(如表2);多数论文采用算术坐标系回归直线，以及存在前面阐述的问题等。

2.3.2 众文章纷纷引用古温标法的剥蚀量作佐证，但该法本身结论就不可信

文献［25］用镜质体反射率(R0)、甾烷成熟参数(SM)等古温标法，计算三垛组剥蚀量在700～2 200 m;此观点被众作者引为佐证。该文立论有两点:①斜坡、深凹不同构造单元的R0－H、SM－H关系存在斜率相近、值不等的几个线状台阶变化，据此建立了三种成熟度模式;②三垛组沉积末、剥蚀前古温标参数基本定型，新近系和第四系影响微弱，由此建立计算剥蚀量模型。

分析认为，该文方法有误、立论无据:①R0－H和SM－H均为对数关系，在半对数坐标系中为线性相关。该文用算术坐标直线关系显然是错误的。本文按不同构造单元和层系，在半对数坐标系上重作R0－H关系图版，发现所谓“台阶”全部消失;②烃源岩沉积后，经历统盆解体的吴堡事件，整盆抬升长期暴露的三垛事件及真武、樊川、东台等抬升事件，形成隆坳、凸凹相间的箕状断陷，铸就了烃源岩差异演化和复杂的R0、SM古温标展布特点;在三垛组不整合面之上无任何古温标参数情况下，拿多个不整合面下伏的古温标参数，推定古温标定型于三垛组沉积末及后期埋藏无影响，缺乏足够证据。相反，从R0－H各分区图或总图的相关性看，除海安凹陷相关性稍差外，其它图的相关系数都良好，且相关直线上延至地表，R0值在0.2%左右，符合公认的原始地表附近R0理论值。这充分表明，历次剥蚀间断面之后的再埋藏已经愈合前期R0为一条直线，也说明间断面剥蚀幅度都小于后期再沉积厚度，证明此类情况不能运用R0、SM古温标计算剥蚀量。

2.3.3 现有各种剥蚀量与苏北盆地实际都不吻合

上述各文剥蚀量恢复后，盆地出现不平衡:一是盆地结构不平衡。苏北盆地三垛组为箕状断陷，自深凹向斜坡到凸起逐渐减薄，这是地震和钻井资料证实的，也是公认的。前述的各种剥蚀量恢复后，三垛组原型盆地变为近等厚平板状结构，有些斜坡和凸起厚度还大于深凹的，出现控凹边界断裂变为逆断层、深凹与凸起构造反转的情况。二是盆地物源与沉积体系不平衡。沉积相反映，建湖隆起为南、北箕状断陷三垛组的物源区;而上述诸文认为该区剥蚀量最大，恢复地层最厚。

由此可见，现有的声波时差法、古温标法，计算的苏北盆地各种剥蚀量结论都是错误的。事实上，按照R0－H明显受晚期埋藏影响判断，三垛组最大剥蚀量不会超过后期的新近系和第四系总厚度。

3 结论

(1)经典Magara法及使用前提是正确的。牟—周的扩展缺乏理论依据和可操作性，不能使用;所有Hx＞Hb情况的剥蚀量恢复数据都是不可信的。

(2)声波时差法、古温标法都不适合计算苏北盆地各个不整合面剥蚀量，现有剥蚀量数据不能用;三垛组剥蚀量小于新近系和第四系总厚度。

［1］ Magara K.Thickness of removed sedimentary rocks，paleopore pressure，and paleotemperature，southwestern part of Western Canada Basin.AAPG(Bull)，1976，60(4):554 －565.

［2］ 真柄钦次．压实与流体运移［M］．陈荷立，译.北京:石油工业出版社，1981.

［3］ 刘景彦，林畅松，喻岳钮，等.用声波测井资料计算剥蚀量的方法改进［J］．石油实验地质，2000，22(4):302 －306.

［4］ 牟中海，陈志勇，陆廷清，等.柴达木盆地北缘中生界剥蚀厚度恢复［J］．石油勘探与开发，2000，27(1):35 －37.

［5］ 周瑶琪，吴智平．地层间断面的时间结构研究［M］．北京:地质出版社，2000.

［6］ 鲁雪松，马淑芳，杨贵丽.苏北盆地金湖凹陷三垛组剥蚀厚度恢复及意义［J］．西南石油大学学报(自然科学版)，2009，31(4):13－17.

［7］ 杨玉平，钟建华，段宏亮.高邮凹陷吴堡断裂带南段古近系剥蚀量计算及地质意义［J］．新疆石油地质，2012，33(4):453－455.

［8］ 能源，杨桥，张克鑫，等.苏北盆地高邮凹陷晚白垩世—新生代构造沉降史分析与构造演化［J］．沉积与特提斯地质，2009，29(2):25－32.

［9］ 徐田武，王英民，魏水建，等.苏北盆地始新统三垛运动剥蚀厚度恢复［J］．石油天然气学报，2008，30(6):56 －60.

［10］ 杨立干，陆英，陈平原.高邮凹陷上下第三系之间地层剥蚀量的研究［J］．江汉石油学院学报，2003，25(增刊下):33－34.

［11］ 刘小平，杨立干，徐健.苏北盆地高邮凹陷始新统剥蚀厚度恢复［J］．新疆石油地质，2004，25(2):128 －130.

［12］ 鲁雪松，蒋有录，常振恒，等.东濮凹陷东营组地层剥蚀厚度估算及其意义［J］．地质科技情报，2001，7(1):8 －12.

［13］ 付晓飞，李兆影，卢双舫，等.利用声波时差资料恢复剥蚀量方法研究与应用［J］．大庆石油地质与开发，2004，23(1):9－11.

［14］ 尚可耕，贾健谊，周祖翼，等.利用声波测井数据估算西湖凹陷地层剥蚀量［J］．海洋石油，2001，109(3):12 －12.

［15］ 吴智平，刘继国，张卫海.辽河盆地东部凹陷北部地区新老第三纪界面地层剥蚀量研究［J］．高校地质学报，2001，7(1):99－105.

［16］ 韩用兵，王良书，刘劭文.渤海湾盆地济阳坳陷沙四段和孔店组地层剥蚀厚度恢复［J］．高校地质学报，2004，10(3):440－448.

［17］ 卢明国，童小兰.江陵凹陷新老第三纪间断面地层剥蚀厚度研究［J］．矿物岩石，2004，24(1):93 －96.

［18］ 王子煜，张明利.东海西湖凹陷新生界主要不整合面地层剥蚀厚度恢复［J］．地质论评，2005，51(3):309 －317.

［19］ 杨雪，杨桥，于福生.辽河盆地西部凹陷北部地区古近系地层剥蚀量恢复［J］．西安石油大学学报，2006，21(5):34 －37.

［20］ 彭清华，周江羽，揭异新.声波时差法对南堡凹陷东营组剥蚀量的恢复［J］．断块油气田，2009，16(6):50－53.

［21］ 翁望飞，刘池洋，赵红格，等.鄂尔多斯盆地早白垩世剥蚀地层厚度恢复研究［J］．地层学杂志，2009，33(4):373 －379.

［22］ 翁望飞，王建强，张蓉蓉.利用声波测井技术计算地层剥蚀厚度——以鄂尔多斯盆地为例［J］．新疆石油地质，2011，32(2):143－146.

［23］ 沈忠民，刘阳，刘四兵.川西坳陷中段喜山期剥蚀厚度恢复

［J］．物探化探计算技术，2011，33(2):189 －194.［24］ 乐昌硕.岩石学［M］．北京:地质出版社，1984.

［25］ 陈安定.苏北第三系成熟演化指标与深度关系的3种模式［J］．石油实验地质，2003，25(1):58 －63.

①戴俊生，马晓鸣，季宗镇，等.高邮凹陷南部断阶带构造演化及成因机制研究［R］．2005，江苏油田.

②傅强，夏岩，丁林林，等.韦一马复杂断裂带沉积特征及成藏控制因素研究［R］．2013，江办油田.