梁端转角对轨道结构受力的影响规律分析
2015-06-07秦艳
秦 艳
(中铁上海设计院集团有限公司,上海 200070)
梁端转角对轨道结构受力的影响规律分析
秦 艳
(中铁上海设计院集团有限公司,上海 200070)
建立了梁端转角引起的扣件系统附加力和钢轨附加力的有限元分析模型,探讨了梁端转角下扣件的受力特征及影响因素,并对满足扣件正常工作的梁端转角大小与梁端转角引起的钢轨附加力进行了计算研究,得出了一些有价值的结论。
梁端转角,轨道,受力,扣件
0 引言
支承块承轨台式无砟轨道是轨道交通高架线上主要的轨道结构形式,这种轨道结构道床刚度大,桥梁的微小变形都将影响轨道结构受力。城市轨道交通桥上线路普遍采用小阻力扣件,扣件弹条的初始扣压力相对较小,有必要对梁端转角限值进行限定以避免弹条破坏而导致扣件失效。此外,梁端转角还将导致梁端钢轨承受较大附加弯矩。本文将探讨梁端转角对轨道结构受力影响的基本规律。
1 梁端转角对扣件受力的影响分析模型
采用通用有限元程序ANSYS建立桥梁—支承块承轨台无砟轨道结构扣件系统受力分析模型,模型如图1所示。梁中心线距离轨面高度为Ht,距离支座高度为Hb,梁端悬臂长为Lc;自梁缝开始,左侧扣件编号依次为-1,-2,-3,…,右侧扣件编号依次为1,2,3,…。如无说明,有限元模型中梁端悬臂长和梁缝宽度分别取0.6 m和0.06 m,以下提及的转角均指梁体在支座点处的转角。
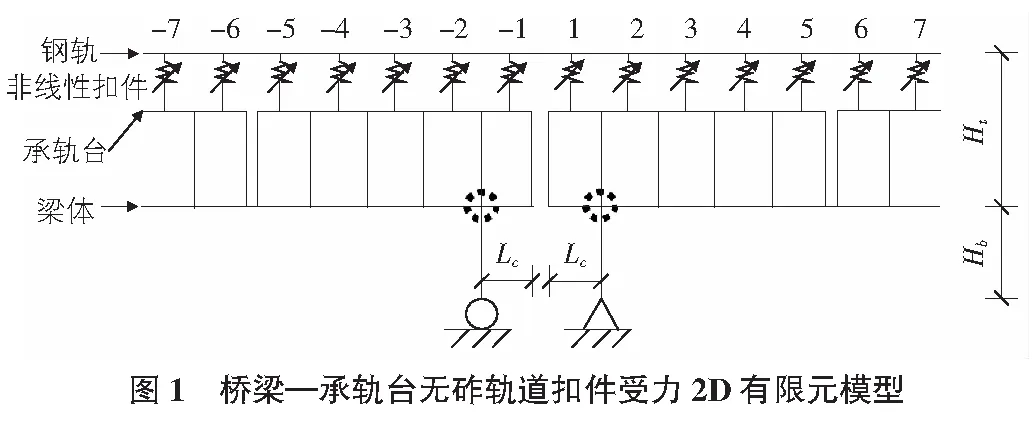
为减小无缝线路钢轨纵向附加力,城市轨道交通桥上线路普遍采用小阻力扣件,WJ-2A型扣件就是一种专门为轨道交通桥上线路设计出来的小阻力扣件,在轨道交通建设中得到了广泛的运用。WJ-2A型小阻力扣件主要参数见表1。

表1 WJ-2A型小阻力扣件主要参数
2 梁端转角下扣件受力特征及影响因素
2.1 扣件受力基本特征
如图2所示为两侧桥梁单侧(左侧梁体转动)和对称转动不同角度时,梁缝两侧扣件受力的变化情况。
由图2可见,各扣件受力均随转角增大而增大,但转角大小的变化几乎不改变梁缝两侧扣件受力的分布规律。梁体单侧转动时,转动侧梁体上离梁端最近的扣件(-1号扣件)承受最大下压力,另一侧梁体上离梁端最近的扣件(1号扣件)承受最大上拔力。两侧梁体对称转动时,扣件受力呈对称分布,离梁缝最近的扣件(-1和1号扣件)承受最大下压力,-3和3号扣件承受最大上拔力。梁端转角1‰rad时,扣件最大上拔力小于初始扣压力8 kN,当梁端转角达到3‰rad时,最大上拔力超出初始扣压力。
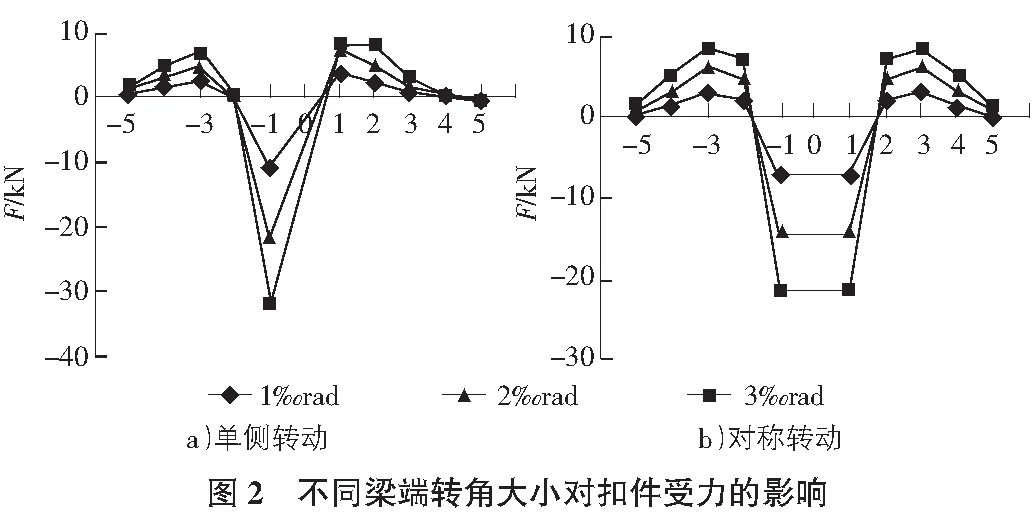
图2计算结果还表明,梁端转角对扣件受力的影响范围限于梁缝两侧各5个扣件,其余扣件力很小。也就是说,相同转角情况下,梁端扣件受力主要受梁端部约3 m长度范围内梁体变形的影响。
2.2 扣件受力影响因素
梁端对称转动1‰rad时,不同扣件间距和胶垫刚度情况下,扣件所受上拔力和下压力最大值如表2,表3所示。减小扣件间距和增大胶垫刚度均增大了梁轨连接刚度,随扣件间距的减小和胶垫刚度的增大,扣件最大上拔和下压力均增大。由于扣件间距的可调范围很小,其对扣件受力的影响有限。胶垫刚度可调范围较大,其对扣件受力的影响也相对较大,当由于老化等原因使胶垫刚度增大时,将对扣件受力产生不利影响。

表2 不同扣件间距下扣件最大上拔和下压力

表3 不同胶垫刚度下扣件最大上拔和下压力
桥梁单侧转动时,梁端悬臂长度将对扣件受力产生较大影响。图3a)为不同悬臂长度情况下左侧梁体转动1‰rad时,梁缝两侧扣件受力分布情况。当悬臂上布置有扣件时(即悬臂长度大于0.3 m),梁体转动使悬臂端上梁体上抬,给其上扣件锚固点施加了向上支座位移,悬臂段越长,该支座位移值越大,因此-1号扣件上最大下压力随悬臂长度增大而增大。而转动侧悬臂段上扣件系统带动钢轨向上位移,钢轨发生局部隆起,钢轨的隆起使非转动侧梁上扣件受拉,悬臂长度越大,这种现象越明显。从图3a)中可以看到,随着悬臂长度的增大,-1号扣件由承受下压力逐渐变为承受最大上拔力,当悬臂长增至0.9 m时,1号扣件上拔力(8.433 kN)超出初始扣压力。
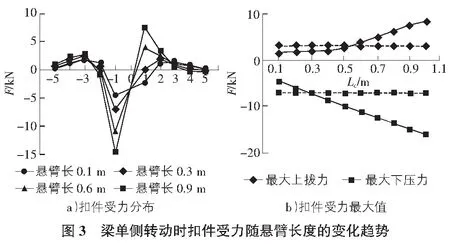
扣件最大上拔和下压力随悬臂长度的变化情况如图3b)所示。图中同时给出了两侧桥梁对称转动相同角度下扣件最大上拔和下压力结果(以虚线表示)。可见两侧梁体对称转动的情况下,扣件受力随悬臂长度的变化很小。
对于单侧转动情况,当悬臂长度较小时,单侧转动下扣件的最大上拔和下压力均小于对称转动情况;随着悬臂长度的增大,扣件的最大上拔和下压力均增大,当悬臂长度大于0.3 m(扣件间距之半,即悬臂上开始有扣件布置)时,单侧转动扣件最大下压力超出对称转动情况,当悬臂长度大于0.5 m时,单侧转动扣件最大上拔力超出对称转动情况。
梁缝两侧梁体单侧和对称转动是梁体变形的特殊情况,一般情况下两侧梁体发生非对称转动,显然,该情况下扣件受力介于单侧转动和对称转动之间。因此,在梁端可能发生的所有转角工况中,当悬臂长度较小时,两侧对称转动对扣件受力最不利;当悬臂长度达到一定值后,单侧转动对扣件受力最不利。
3 满足扣件正常工作的梁端转角大小
梁端扣件除受到梁端变位引起的附加力外,还承受列车荷载的直接作用力。轴重140 kN地铁小型列车设计荷载作用下,按照弹性点支承模型计算得到的扣件最大上拔力和下压力随胶垫刚度的变化如图4所示,最大上拔力和最大下压力均随胶垫刚度的增大基本成线性增长关系。
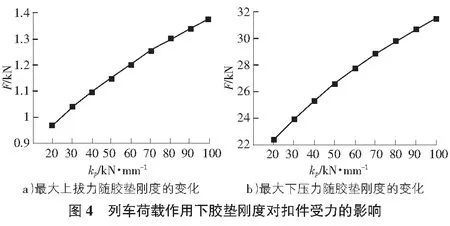
对于无砟轨道而言,扣件几乎是轨道弹性和调整能力的唯一提供者,其结构的强度、耐久性和弹性直接关系到列车走行性。因此应限制端变位幅值,确保梁端扣件的正常工作。由于胶垫刚度kp远大于弹条刚度kc,下压力限值比上拔力限值大得多,一般不会出现扣件下压力过大的情况,通常满足上拔力限值即可保证扣件系统正常工作。设列车荷载引起的扣件最大上拔力为Fv,扣件初始扣压力为2Fc。则梁端变位产生的扣件最大上拔力限值[F]=2Fc-Fv,由此确定的不同胶垫刚度下,梁端对称转角限值见表4。
由表4可见,对称转角限值均不小于1‰rad,胶垫刚度越小限值越大,通常情况下,胶垫刚度取通常值kp=40 kN/mm~60 kN/mm时,对称转角限值可取为2.0‰rad(单侧),严于相关规范3.0‰rad的规定。需要说明的是,实际桥梁轨道结构及桥梁支座均有一定变形能力,有限元计算得到的梁端变位限值将偏于保守。

表4 满足扣件正常工作的梁端对称转角限值
不同悬臂长度下单侧转角限值随胶垫刚度的变化趋势如图5所示,图中虚线表示对称转角限值。可见当悬臂长度小于0.5 m时,对称转角限值比单侧转角限值要求高;当悬臂长度大于0.5 m时,单侧转角限值比对称转角限值要求要高。对于中小跨度简支梁,从保证扣件受力的角度出发,建议梁端悬臂长度不超过0.5 m。
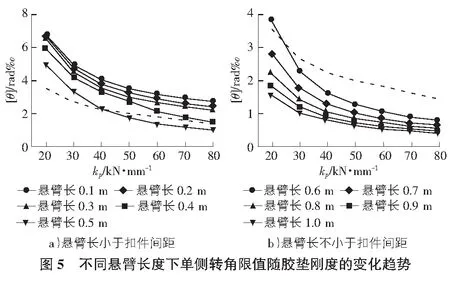
4 梁端转角引起的钢轨附加力
钢轨是在扣件节点处散点支承的,令模型单侧梁体转动1‰rad,不同悬臂长度下,梁端钢轨最大曲率Kmax随胶垫刚度kp的变化趋势如图6所示。
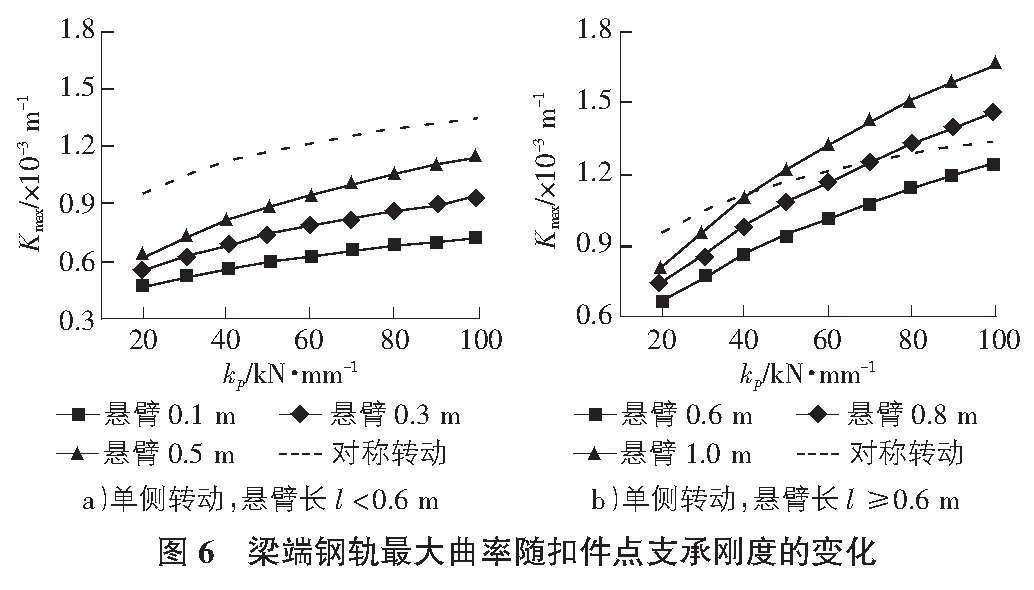
由图6可见,梁端钢轨最大曲率随胶垫刚度增大而增大;梁体单侧转动时,梁端悬臂段长度对钢轨曲率的影响很大,梁端悬臂越长曲率越大,且最大曲率随胶垫刚度的增长速率也越大;当悬臂长度l
分析结果表明,桥梁梁端发生单侧转动时,悬臂段越长,胶垫刚度越大,梁缝处钢轨“局部隆起”现象越明显,该处钢轨曲率越大,钢轨承受的附加弯矩也越大。
5 结语
本文首先建立了梁端转角引起的扣件系统附加力和钢轨附加力有限元分析模型,在此基础上对两者分布规律和影响因素进行了具体分析,最后提出了在轴重140 kN的地铁小型车设计荷载作用下,满足扣件正常受力要求的梁端转角限值,得到结论如下:
1)梁端转角对扣件受力的影响范围限于梁缝两侧各5个扣件,其余扣件力可忽略。梁体单侧转动时,转动侧梁体上离梁端最近的扣件下压力最大,另一侧梁体上离梁端最近的扣件上拔力最大。两侧梁体对称转动时,扣件受力呈对称分布,离梁缝最近的扣件下压力最大,自梁缝开始第3个扣件上拔力最大。
2)随扣件间距的减小和胶垫刚度的增大,扣件最大上拔和下压力均增大。扣件间距的可调范围很小,其对扣件受力的影响有限。胶垫刚度可调范围较大,其对扣件受力的影响相对较大。
3)桥梁单侧转动时,梁端悬臂长度越大,扣件受力越不利,当悬臂长度超过扣件间距时,单侧梁体转动引起的上拔力最大值将超过两侧对称转动情况。
4)梁端发生单侧转动时,悬臂段越长,胶垫刚度越大,梁缝处钢轨承受附加弯矩越大。
5)为满足梁体结构和梁端伸缩缝设计的需要,大跨度桥梁端一般悬臂较长、梁缝较大。在同样的梁端转角下,这类桥梁对轨道结构受力较不利。
[1] 赵坪锐,肖杰灵,刘学毅.梁端位移对无碴轨道扣件系统的影响分析[J].铁道学报,2008,30(5):68-72.
[2] 李志红.广珠城际轨道交通梁端轨道结构受力变形分析[J].铁道建筑,2009(10):95-97.
[3] 丁敏旭.客运专线无碴轨道梁端扣件上拔力研究[J].科学技术与工程,2011(16):3709-3713.
On law analysis of influence of rotation angles of bridge beams on rail structural stress
Qin Yan
(ChinaRailwayShanghaiDesignInstituteGroupCo.,Ltd,Shanghai200070,China)
The paper establishes the finite element analysis models for fastener system and steel rail additional forces caused by the rotation angles of bridge beams, explores the stressed features and influential factors of the fasteners under the rotation angles of bridge beams, undertakes the calculation and research on the sizes of the rotation angles to meet the normal working of fasteners and the steel rail additional force caused by the rotation angles of bridge ends, and achieves some beneficial conclusion.
rotation angle of bridge end, rail, stress, fastener
2014-12-17
秦 艳(1983- ),女,工程师
1009-6825(2015)06-0176-03
U441
A
