等级Voronoi图及加权Voronoi图的ArcGIS矢量生成算法

田 松，崔 希 民，孙 云 华，宫 宇

(1.中国矿业大学(北京)地球科学与测绘工程学院，北京 100083；2.国家海洋局南海分局，广东 广州 510310)



等级Voronoi图及加权Voronoi图的ArcGIS矢量生成算法

田 松1，崔 希 民1，孙 云 华1，宫 宇2

(1.中国矿业大学(北京)地球科学与测绘工程学院，北京 100083；2.国家海洋局南海分局，广东 广州 510310)

等级Voronoi图及加权Voronoi图是以树状形式表达事物层次关系的方法，可作为一种空间数据模型应用于城镇等级体系、组织结构关系表达等地学领域。该文首次提出一种等级Voronoi图及加权Voronoi图的ArcGIS矢量生成算法，以ArcGIS Engine为开发工具，利用增量法思想，通过区域分割和合并方法实现了对空间的多级划分，为研究和发展GIS空间数据模型提供了重要的方法手段。

等级Voronoi图；等级加权Voronoi图；ArcGIS；区域分割；区域合并

0 引言

等级Voronoi图(Hierarchical Voronoi Diagram)亦称作分层Voronoi图，简称等级V图或分层V图,是对空间区域多级划分，以树状形式表示区域层次关系的方法，是Voronoi图理论和应用的扩展。等级V图是一种数据结构，用于提高数据组织、检索及可视化效率，亦是一种空间数据模型，用于表达空间事物间的等级层次关系。Farin等[1]利用等级V图进行地形建模;Gold等[2]将等级V图用于地形数据的组织与LOD显示;Wallgrün[3]利用等级V图解决了机器人路径搜索问题；赵威、陈笑筑、薛莹等[4-6]分别利用等级V图表达了开封市、毕节市、苏浙沪城市群的城市等级体系。

等级加权Voronoi图(等级加权V图)是等级Voronoi图的扩展，是在考虑母点权重的情况下，划分多级空间的方法。Balzer等[7]研究了等级V图及加法加权等级V图的生成算法，并用于软件度量可视化；Sud等[8]利用CPU加速技术实现了加法加权的等级V图；Kang等[9]利用等级加权V图进行空间数据的组织和管理。目前，尚无结合GIS软件或工具实现等级V图及加权图的方法。本文在文献[10]方法的基础上，利用ArcGIS Engine(简称AE)实现了等级V图及加权V图的矢量生成方法，旨在建立一种适用于地学领域的空间数据模型，为表达空间事物的多级层次关系提供一种良好的可视化手段。

1 定义

1.1 等级V图定义[9]

定义1：Vh(P)={Vh(p1),Vh(p2),…,Vh(pn)}是以pi(i=1,2,…,n)为母点的Voronoi图，h表示等级，h=1时等级最高，Vh(pi)表示母点pi的Voronoi区域(简称V区域)，令点集Qi={qj|qj∈Vh(pi),j≥1,1≤i≤n}，若Voronoi图Vh+1(Qi)和Vh(pi)存有如下关系：

Vh+1(Qi)={Vh+1(qj)|Vh+1(qj)⊂Vh(pi),

qj∈Vh(pi),j≥1,1≤i≤n}

(1)

且有∑Vh+1(qj)≡Vh(pi)，则称Vh(P)为等级Voronoi图。公式为：

Vh(P)={Vh+1(Q1),Vh+1(Q2),…,Vh+1(Qn)}

(2)

1.2 等级加权V图定义

定义2：Vh(P,λ)={Vh(p1,λ1),Vh(p2,λ2),…,Vh(pn,λn)}是以pi(i=1,2,…,n)为母点、λi为权重的加权Voronoi图，Vh(pi,λi)表示母点pi的加权Voronoi区域(简称加权V区域)，令点集Qi={qj|qj∈Vh(pi,λi),j≥1,1≤i≤n}，若加权Voronoi图Vh+1(Qi,λ)和Vh(pi,λi)存在如下关系：

Vh+1(Qi,λ)={Vh+1(qj,λj)|Vh+1(qj,λj)⊂Vh(pi,λi),

qj∈Vh(pi,λi),j≥1,1≤i≤n}

(3)

且有∑Vh+1(qj,λj)≡Vh(pi,λi)，则称Vh(P,λ)为等级加权Voronoi图。公式为：Vh(P,λ)={Vh+1(Q1,λ),Vh+1(Q2,λ),…,Vh+1(Qn,λ)}

(4)

为方便后续描述，均用Vh表示第h级V图或加权V图，Vh(i)表示母点pi的V区域或加权V区域。

2 等级V图、加权V图ArcGIS矢量生成算法

2.1 算法基本思想

以等级加权V图为例，设P={p1,p2,…,pn}是二维欧氏空间上的n个母点，λ为母点权重，h为母点等级，相同h值的母点处于同一等级。算法基本思想：生成点集最小外包矩形，用h=1的母点集合划分最小外包矩形，生成加权V图V1；判断h=2的点集归属，并利用该点集划分V1，生成第二层的加权V图V2，以此类推，直至算法结束。

加权V图生成方法为：利用增量法思想，每插入一个点，对原有加权区域进行重新划分，分割出属于新插入点的加权V区域，当所有点插入完成后，即得到最终的加权V图。等级V图是等级加权V图权重相同时的特例，二者算法实现思想相同。

2.2 算法实现步骤

Input:P={p1,p2,…,pn}，pi∈P，包含属性：ID，pi的唯一标识(对应图1中的Belong字段)；Weight，pi权重(对应图1中的Weight字段)，与变量λ意义相同；Level，pi等级(对应图1中的Level字段)，与变量h意义相同。

Output:等级V图、等级加权V图。

图1 ArcGIS点集示例

Fig.1 A set of points saved in ArcGIS attribute table

算法具体步骤如下：

(1)数据获取及预处理。获取母点集合P，并按其Level值划分为不同等级的母点集合pL={pL1,pL2,…,pLm}，pLh∈pL，∑pLh≡P，pL1表示最高层次点集，pLm为最低层次点集。

(2)获取P的最小外包矩形MBR。初始化加权V图结构体V0，并令V0=MBR。

(3)递归循环pLh集合，生成等级加权V图，伪代码如下：

for(inth=1;h≤m;h++){

//获取当前等级点集

pLh=GetLevelPoints(P,h)

//将pLh归属不同加权V区域

Vh-1=SetPnts2BelongRegion(pLh,Vh-1)

//初始化加权V图结构体Vh,_Vh

for(intj=1;j≤VorCount;j++){

//VorCount：当前加权V区域个数

Vh←Vh-1(j)

for(intt=2;t≤VorPntsCount;t++){

//VorPntsCount：加权V区域内包含的点个数

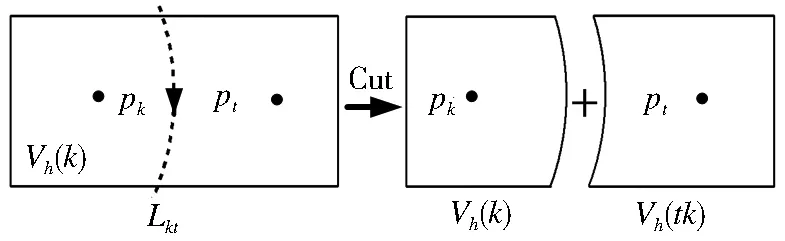
for(intk=1;k

if(pt.Weight=pk.Weight)

//垂直平分线划分区域

Vh(tk)=DivideRegionWithPB(pt,pk,Vh(k))

else//圆弧划分区域

Vh(tk)=DivideRegionWithArc(pt,pk,Vh(k)) }

//区域合并

Vh(tK)={Vh(t1),Vh(t2),…,Vh(tk),…,Vh(tt-1)}

Vh(t)=UnionRegion(Vh(tK))}

Vh←Vh

_Vh=null}

Vh=_Vh

//输出h级加权V图

ExportLevelVorRegion(Vh)}

等级V图伪代码和加权V图类似，由于不需要判断权重，所以只需保留垂直平分线划分区域的方法，即代码改变如下：

for(intk=1;k

Vh(tk)=DivideRegionWithPB(pt,pk,Vh(k))}

其他代码不变。

2.3 算法说明

2.3.1 点集的区域归属判定 第一次循环，SetPnts2BelongRegion()方法认定MBR为点集pL1的V区域或加权V区域V0，利用pL1划分V0生成V1，自第二次循环起，将pLh中的点归属于Vh-1(j)(j=1,2,…,VorCount)。点集归属判别方法：如果pLh中的一个点p∩Vh-1(j)≠Ф，则认为点p属于Vh-1(j)。

2.3.2 区域分割和合并 假定pi(xi,yi)、pj(xj,yj)为空间中两个不重叠的点，λi、λj是两点权重。根据文献[10,11]给出的V图及加权V图定义可知，两点间Voronoi边为一直线，其公式如下：

(5)

两点间加权Voronoi边为一圆弧，其公式如下：

(6)

圆心为：

(7)

半径为：

(8)

式中:d(pi,pj)表示pi和pj间的欧氏距离。

以此数学理论为基础，便可利用AE接口实现点集的加权V区域划分，具体包括4个要点：直线生成、圆弧生成、V区域及加权V区域分割、V区域及加权V区域合并。

(1)直线生成。AE提供ILine接口，包含FromPoint和ToPoint属性用于生成直线，表示通过设定起始点和终止点坐标(通过式(5)和MBR边界求交获得)，生成一条两点间的线段。该方法的具体实现包含在DivideRegionWithPB()方法中。

(2)弧段生成。IConstructCircularArc.ConstructCircle(IPointCenterPoint,doubleRadius)方法可用于生成弧段，其中圆心参数CenterPoint由式(7)获得，半径参数Radius由式(8)获得。该方法的具体实现包含在DivideRegionWithArc()方法中。

(3)区域分割。如图2所示，假设Vh(k)是点pk的加权V区域，pt是插入点，Lkt是pk和pt间的加权Voronoi边，利用AE接口ITopologicalOperator.Cut(IPolylinecutter,refIGeometryleftGeom,refIGeometryrightGeom)方法，可将区域Vh(k)分割为leftGeom和rightGeom两部分，其中，cutter即为Lkt，rightGeom和leftGeom对应Vh(k) (分割后属于pk的加权V区域)和Vh(tk) (从Vh(k)分割出来属于pt的区域)。在AE提供的拓扑分割接口中，参数Cutter即为由ILine和IConstructCircularArc接口生成的直线及弧段。该方法的具体实现包含在DivideRegionWithPB()和DivideRegionWithArc()中。

图2 区域分割

Fig.2Regiondivisionbyanarc

加权V区域分割时，由于考虑权重因素，需判断权重相等及不相等两种情况，从而确定直线分割区域和弧段分割区域两种方法。由于V区域划分不涉及权重因素，所以只需考虑直线分割区域的情况。

(4)区域合并。UnionRegion()方法指定V区域和加权V区域合并方式。如图3，设pk是h级加权V区域Vh(k) 所包含的点，k=1,2,…,c,c=VorPntsCount，若新插入一点pt(t=c+1)，其合并操作步骤如下：计算获得pt与pk的加权Voronoi边{L1t,L2t,…,Lkt,…,Lct}，利用Lkt对应分割{Vh(1),Vh(2),…,Vh(c)}，将分割后属于pt的区域{Vh(t1),Vh(t2),…,Vh(tc)}合并，生成pt的加权V区域Vh(t)。

图3 区域合并

Fig.3 Regions union

2.3.3 等级加权V图输出 ExportLevelVorRegion()方法指定等级加权V图的输出方式：对于每一层级点集pLh，输出对应的加权V图Vh，并以矢量图形式存储。将输出图层叠加，即可显示最终的等级加权V图效果。

3 应用实例

图4、图5为等级V图及加权V图示例，其中母点集合为{pL1,pL2,pL3,pL4}，分别对应于图例中大圆、正方形、三角形、小圆所代表的点集，其中pL1包含4个母点，pL2包含10个母点，pL3包含11个母点，pL4包含125个母点。结果为四级等级V图及加权图{V1,V2,V3,V4}，边界粗细程度代表等级程度差异，边界越粗，等级越高。生成图4所示的等级V图平均用时5.21 s，生成图5所示的等级加权V图平均用时33.08 s。造成时间差异的主要原因是生成加权V图时拓扑分割和合并操作要比生成V图复杂，所以用时较长。

4 结论

图4 等级V图 图5 加权等级V图

Fig.4 HVD Fig.5 HMWVD

本文在文献[10]的基础上首次实现了等级V图及加权V图的ArcGIS矢量生成算法，该算法有如下特点：1)提供了一种适用于地学领域的空间数据模型，应用该算法可以方便地建立等级V图及加权V图，用以表达城镇等级体系、机构布局设置、区域层次差异等内容，丰富了Voronoi图在地学领域的应用。2)利用ArcGIS提供接口，以拓扑分割合并方式实现算法，精度高，实用性强。生成的等级V图及加权V图和原始生成元文件可以组合存储于GIS空间数据库中，便于管理，同时可以灵活地更改点、面样式，丰富输出结果的表达方式。等级V图及加权V图以矢量方式生成，以方便与其他矢量或栅格数据进行叠加分析，挖掘更深层次的隐含信息。

[1] FARIN G,HAGEN H,HAMANN B.Hierarchical and Geometrical Methods in Scientific Visualization[M].Springer,2001.

[2] GOLD C,ANGEL P.Voronoi hierarchies[A].Proceedings of Geographic Information Science-4th International Conference,Geoscience[C].2006.99-111.

[3] WALLGRÜN J O.Hierarchical Voronoi Graphs-Spatial Representation and Reasoning for Mobile Robots[D].Germany:University of Bremen,2008.

[4] 赵威，张仲元，秦耀辰,等.基于Voronoi图的开封市域城镇影像范围和等级体系研究[J].河南大学学报(自然科学版)，2008，38(8)：271-275.

[5] 陈笑筑，王博，胡伟.基于Voronoi图的乡镇等级体系划分及影响范围研究——以毕节市为例[J].安徽农业科学，2011，39(35)：21947-21949.

[6] 薛莹，俞路，韩贵峰.基于Voronoi图剖分的区域旅游中心城市体系——以苏浙沪地区为例[J].地域研究与开发，2008，27(4)：81-84.

[7] BALZER M,DEUSSEN O.Voronoi treemaps[A].Proceedings of the 2005 IEEE Symposium on Information Visualization[C].IEEE Press,2005.

[8] SUD A,FISHER D,LEE H P.Fast dynamic voronoi treemaps[A].Proceedings of the 2010 International Symposium on Voronoi Diagrams in Science and Engineering (ISVD′10)[C].2010.85-94.

[9] KANG S,LI J T,ZHANG F Q,et al.Hierarchical weighted Voronoi tessellations on visual application of spatial data[J].Journal of Computational Information Systems,2013,9(18):7341-7348.

[10] 范熙伟.加权Voronoi图矢量生成算法研究及其实现[D].西安：西北大学，2011.21-35.

[11] 张有会.加权Voronoi图的画法研究[J].计算机科学，2001，28(6)：126-130.

Vector-Based Realization of Hierarchical Voronoi Diagram and Multiplicatively Weighted Voronoi Diagram with ArcGIS

TIAN Song1,CUI Xi-min1,SUN Yun-hua1,GONG Yu2

(1.CollegeofGeoscienceandSurveyingEngineering,ChinaUniversityofMiningandTechnology,Beijing100083; 2.SouthChinaSeaBranch,StateOceanicAdministration,Guangzhou510310,China)

Hierarchical Voronoi diagram (HVD) and hierarchical multiplicatively weighted Voronoi diagram (HMWVD) are methods of expressing hierarchical relationships in the form of trees,which are widely applied in the field of geography,such as urban hierarchies exhibition,organization structures expression,etc.A vector-based approach is first proposed to generate HVD and HMWVD through the methods of regions division and regions union with ArcGIS Engine based on the thought of incremental method.It provides an important way to research and develop GIS spatial data model.

hierarchical Voronoi diagram;hierarchical multiplicatively weighted Voronoi diagram;ArcGIS;region division;regions union

2014-05-13；

2014-07-08

国家自然科学基金项目(71150001)

田松(1985-)，男，博士研究生，研究方向为GIS算法研究。E-mail：tsisatc@163.com

10.3969/j.issn.1672-0504.2015.02.008

P208

A

1672-0504(2015)02-0034-04