电涡流缓速器涡流折算系数的计算方法

胡东海，何 仁，汤 宝

(江苏大学 汽车与交通工程学院，江苏 镇江 212013)



电涡流缓速器涡流折算系数的计算方法

胡东海，何 仁，汤 宝

(江苏大学 汽车与交通工程学院，江苏 镇江 212013)

分析了涡流折算系数对电涡流缓速器制动力矩理论计算的影响。通过对两种型号电涡流缓速器制动力矩实验数据的分析，建立了关于涡流折算系数的微分方程。利用MATLAB直接搜索工具箱得到微分方程的初值条件，再通过龙格-库塔法求解该微分方程获得涡流折算系数的数值解。根据这一计算方法对电涡流缓速器制动力矩进行验证计算，计算结果与实验数据基本一致，说明此计算方法是可行的且解决了电涡流缓速器在改型优化和新产品设计中存在的难题。

车辆工程；涡流折算系数；制动力矩计算；龙格-库塔法；电涡流缓速器

0 引 言

电涡流缓速器作为汽车的主要辅助制动装置，已经有了几十年的历史，国内外学者对电涡流缓速器的基础理论进行了深入的研究。其中电涡流缓速器制动力矩的计算作为电涡流缓速器研究的难点一直为国内外学者所关注[1]。国外学者大多利用解析法求解电涡流缓速器的制动力矩：K.Venkataratnam，等[2-3]提出将转子盘或转子鼓的材料参数B/H曲线用公式拟合，综合考虑该曲线以及定子铁芯磁饱和的影响，分别推导出转筒式缓速器和电涡流缓速器的制动力矩模型；S.Sharifaddin，等[4-5]讨论集肤效应对制动力矩的影响，建立了考虑集肤效应的电涡流缓速器制动力矩模型。国内学者主要利用简化计算法推导电涡流缓速器的制动力矩计算公式：何仁，等[6]基于铁棒假设推到了电涡流缓速器的制动力矩计算公式；何建清[7]提出了闭合圆环假设，并结合磁路分析得出了电涡流缓速器的计算公式；杨效军，等[8-9]将闭合圆环假设法运用在转筒式和自励式缓速器的制动力矩的计算上，取得了很好的效果。

笔者为了解决电涡流缓速器制动力矩计算模型中涡流折算系数求解的问题，通过对两种型号的电涡流缓速器制动力矩实验数据的分析，建立了关于涡流折算系数的微分方程。利用MATLAB直接搜索工具箱得到微分方程的初值条件，再通过龙格-库塔法求解该微分方程获得涡流折算系数的数值解。

1 涡流折算系数

笔者所关注的工程现象是由集肤效应以及去磁效应共同引起的电涡流缓速器气隙磁场变化的问题。当给一个圆形断面的直导体中通入交流电时，导体内部的电流分布并不均匀，导体表面的各点的电流密度最大，导体内的电流密度呈指数递减，导体中心轴线处电流密度几乎为0，这种现象称为集肤效应[10]。励磁磁场产生的电涡流会产生与励磁磁场方向相反的电磁场，对励磁磁场有不同程度的削弱作用，这就是通常所说的去磁效应[11]。在电机学中，这种电枢磁势对气隙磁场的影响称为电枢反应[12]。

这是一种广泛存在的工程现象在各个学科都进行了深入的研究：首先是前苏联的C.B.瓦修京斯基[11]对变压器的涡流损耗的研究，讨论了集肤效应对涡流损耗的影响，同时也提出了详细计算涡流去磁效应的方法；汤蕴璆[12-13]利用解析法电机内的涡流分布，综合考虑了集肤效应对电机涡流分布的影响；左俊业，等[14-15]讨论了涡流制动器有效参数的计算方法以及涡流测功机的设计方法，提出了将电枢反应磁通折算到励磁绕组的概念；叶乐志[16]为了寻求建立永磁涡流缓速器的数学模型，根据电机的电枢反应原理和磁路分析方法，运用迭代法计算了永磁涡流缓速器的气隙磁场强度。

电涡流缓速器工作时，转子盘在定子磁场中旋转，转子盘上与定子磁极相对的圆形区域磁通量按照正弦变化，在转子盘表面内产生感应涡流。根据法拉利电磁感应定律，感应涡流与定子磁场相互作用会产生的制动力矩,如图1。

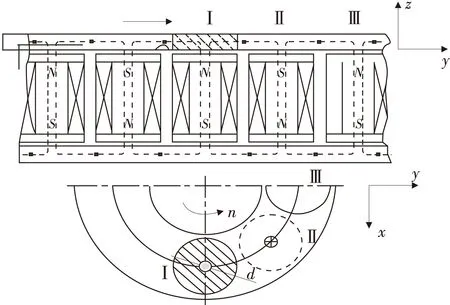
图1 电涡流缓速器磁场示意

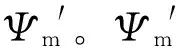
(1)

式中：Ψe为涡流产生的等效磁动势，Ψe=Ke·Ie(Ie为计算区域的涡流有效值)。

根据以上分析求得电涡流缓速器气隙磁感应强度[17]为：

(2)

电涡流缓速器的制动力矩[17]为：

(3)

由式(1)～式(3)可以看出，涡流折算系数的电涡流缓速器制动力矩计算过程中的唯一一个未知系数，该系数的取值正确与否直接影响电涡流缓速器制动力矩计算的有效性。

2 涡流折算系数对电涡流缓速器制动力矩的影响分析

在进行电涡流缓速器改型优化过程中，采用文献[17]所述的制动力矩计算方法进行电涡流缓速器的制动力矩理论计算，该理论计算值与实验值有较大出入。表1列出两组电涡流缓速器的基本参数；两种型号的电涡流缓速器均为同一家扬州洪泉公司生产，电涡流缓速器的材料参数相同，计算得电涡流缓速器的理论计算力矩如表2。

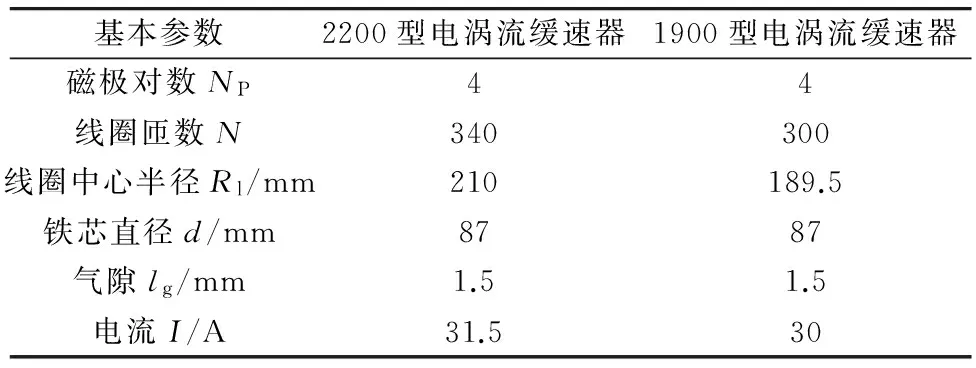
表1 两组电涡流缓速器的基本参数

表2 电涡流缓速器理论力矩与实验力矩

在表2中可以发现，两种型号电涡流缓速器制动力矩预测精度相差很大，1900型电涡流缓速器理论制动力矩与实验值出入较大。在编程求解两种型号电涡流缓速器制动力矩理论计算时取了相同的涡流折算系数Ke=1.6；改变“1900型电涡流缓速器”制动力矩计算程序中的涡流折算系数为Ke=1.2，重新计算其理论制动力矩值得到表3。

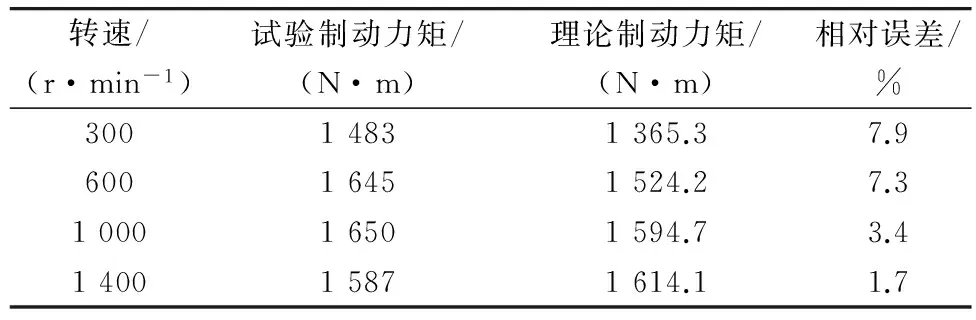
表3 扬州洪泉1900型电涡流缓速器理论力矩与实验力矩

从表3中可以看出，涡流折算系数Ke=1.2时，该计算方法对制动力矩的预测精度有了很大的改善。文献[18]中提出涡流折算系数Ke=0.8～1.8，为此在图2中给出了不同的涡流折算系数Ke预测出的1900型电涡流缓速器的制动力矩计算曲线。Ke=1.2时预测得到的制动力矩值比较符合实际的实验值，Ke的取值越小所预测得到的制动力矩值越大，这与式(1)～式(3)中理论计算式相符；尽管Ke=1.2时，在转速<500 r/min时，预测得到的制动力矩值小于实验值，而在转速>1 100 r/min时，预测得到的制动力矩值有大于实验值的趋势，这表明在整个转速范围内的涡流折算系数取1.2并不合理。同时，可以看出涡流折算系数的选取对电涡流缓速器的制动力矩理论计算值影响很大，目前鲜有关于这个方面的研究工作，这就给电涡流缓速器改进和新产品设计带来问题。

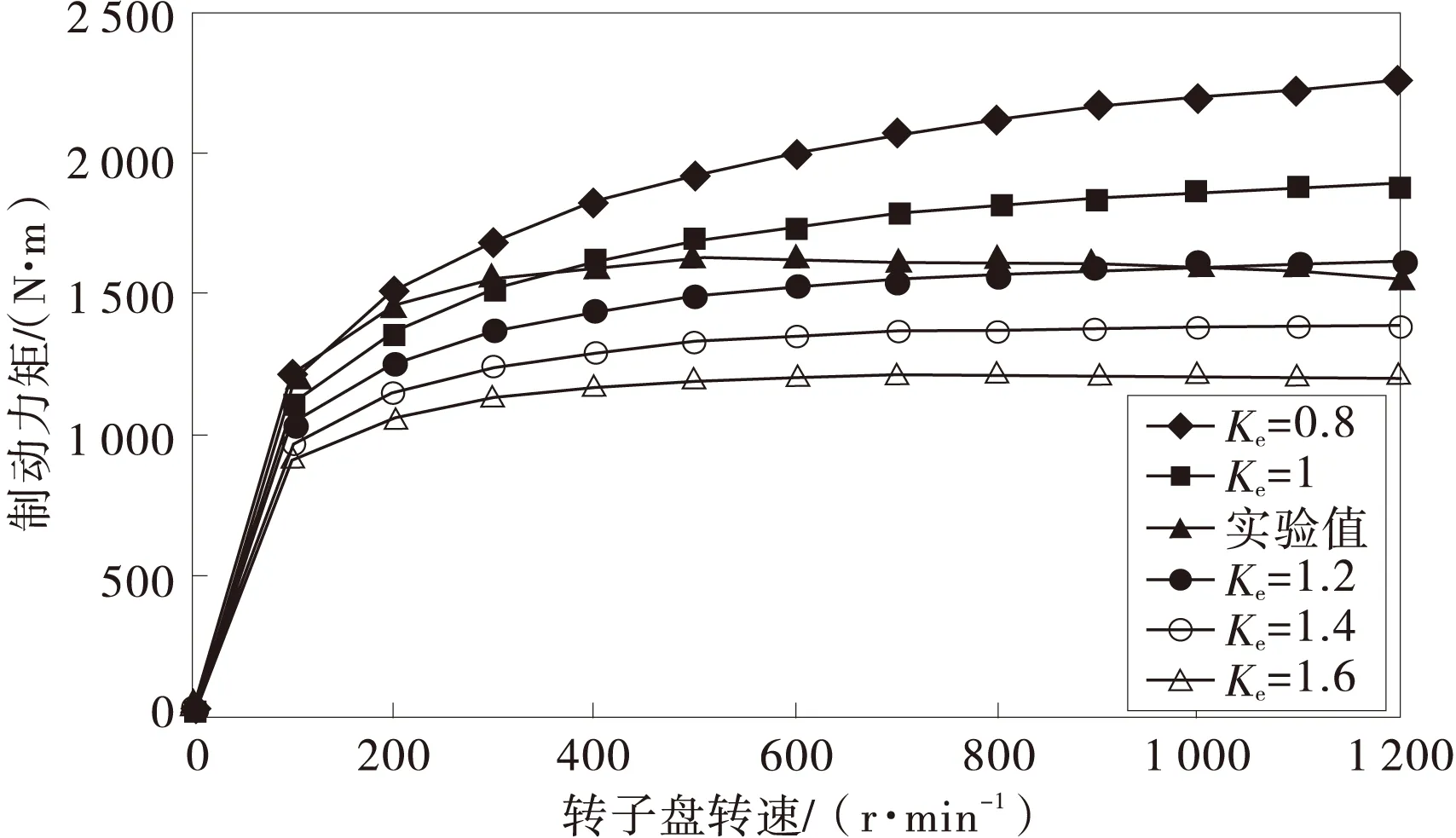
图2 不同涡流折算系数的制动力矩曲线

3 涡流折算系数Ke的计算方法

3.1 两个重要假设

为了研究涡流折算系数Ke的取值规律，观察了两种不同型号的电涡流缓速器的实验数据。这里以江苏省汽车工程重点实验室与扬州市洪泉实业有限公司合作开发的1900型电涡流缓速器和2200型电涡流缓速器为研究对象，研究涡流折算系数Ke的计算方法。

由图3和图4可以看出，同一种型号的电涡流缓速器的制动力矩曲线与涡流折算系数的曲线形状相似；不同型号的电涡流缓速器的在转速100～200 r/min范围内，涡流折算系数曲线的形状相似。因此笔者提出两个假设：

1)同一型号的电涡流缓速器的制动力矩对转速的导数与涡流折算系数导数存在线性关系；

2)不同型号的电涡流缓速器的涡流折算系数随转速变化情况相似。

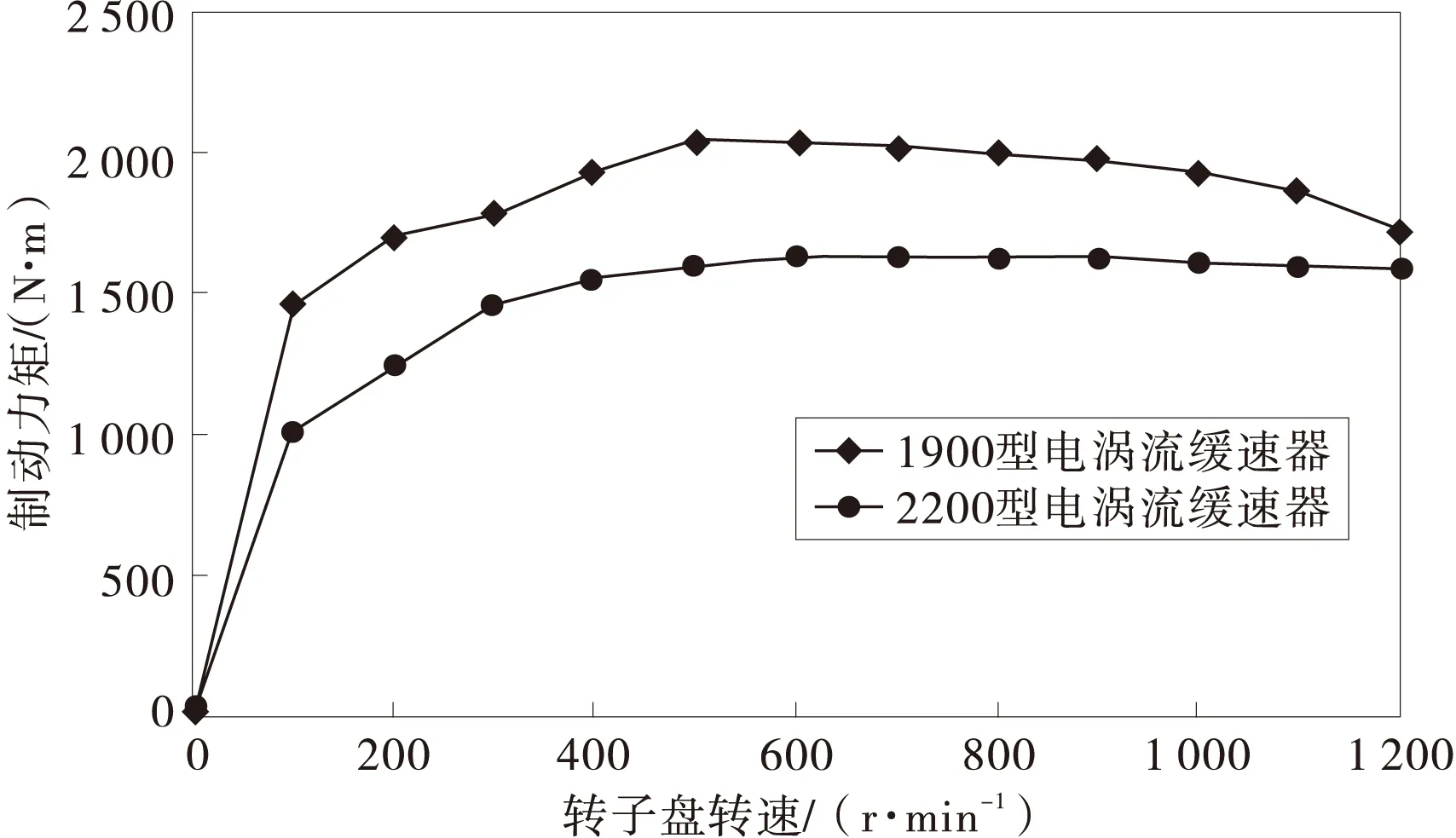
图3 电涡流缓速器制动力矩实验曲线

图4 电涡流缓速器涡流折算系数曲线

T′(n) =Ke′(n)×(-1 000)

(4)

图5 1900型电涡流缓速器制动力矩及涡流折算系数的导数曲线

在图6中看到两种型号电涡流缓速器涡流折算系数对转速的导数大小很接近，因此证明了假设2的成立。这两个假设的证明为下文计算涡流折算系数的大小提供了依据。

图6 两种电涡流缓速器涡流折算系数对转速的导数曲线

3.2 涡流折算系数的计算方法

根据假设1，推导关于涡流折算系数的微分方程。简化式(3)得到电涡流缓速器的制动力矩计算公式[17]：

(5)

气隙磁场的磁场感应强度是由励磁线圈和涡流共同激励而成，其中由励磁线圈产生的磁感应强度为B1、圆环内涡流产生的磁感应强度为B2[7]。气隙磁场的磁场感应强度：

B=B1-B2

(6)

励磁线圈产生的磁动势Ψm由线圈匝数和通入线圈的励磁电流确定，即:

ψm=NI

(7)

式中：N为电磁线圈的线圈匝数； I为通入励磁线圈的励磁电流，A。

得出励磁线圈在气隙中产生的磁感应强度:

(8)

同理得出转子盘表面内涡流在气隙中产生的磁感应强度:

(9)

(10)

综合式(6)、式(8)、式(10)得到气隙磁场的磁感应强度为：

(11)

由上面分析可知，涡流折算系数Ke与制动力矩T对转速n的导数存在线性关系。将涡流折算系数Ke与制动力矩T对转子盘转速n求导：

(12)

(13)

运用龙格-库塔法(Runge-Kutta)求该微分方程的数值解，在MATLAB中编写程序求得涡流折算系数Ke理论计算值与实验值的曲线如图7。

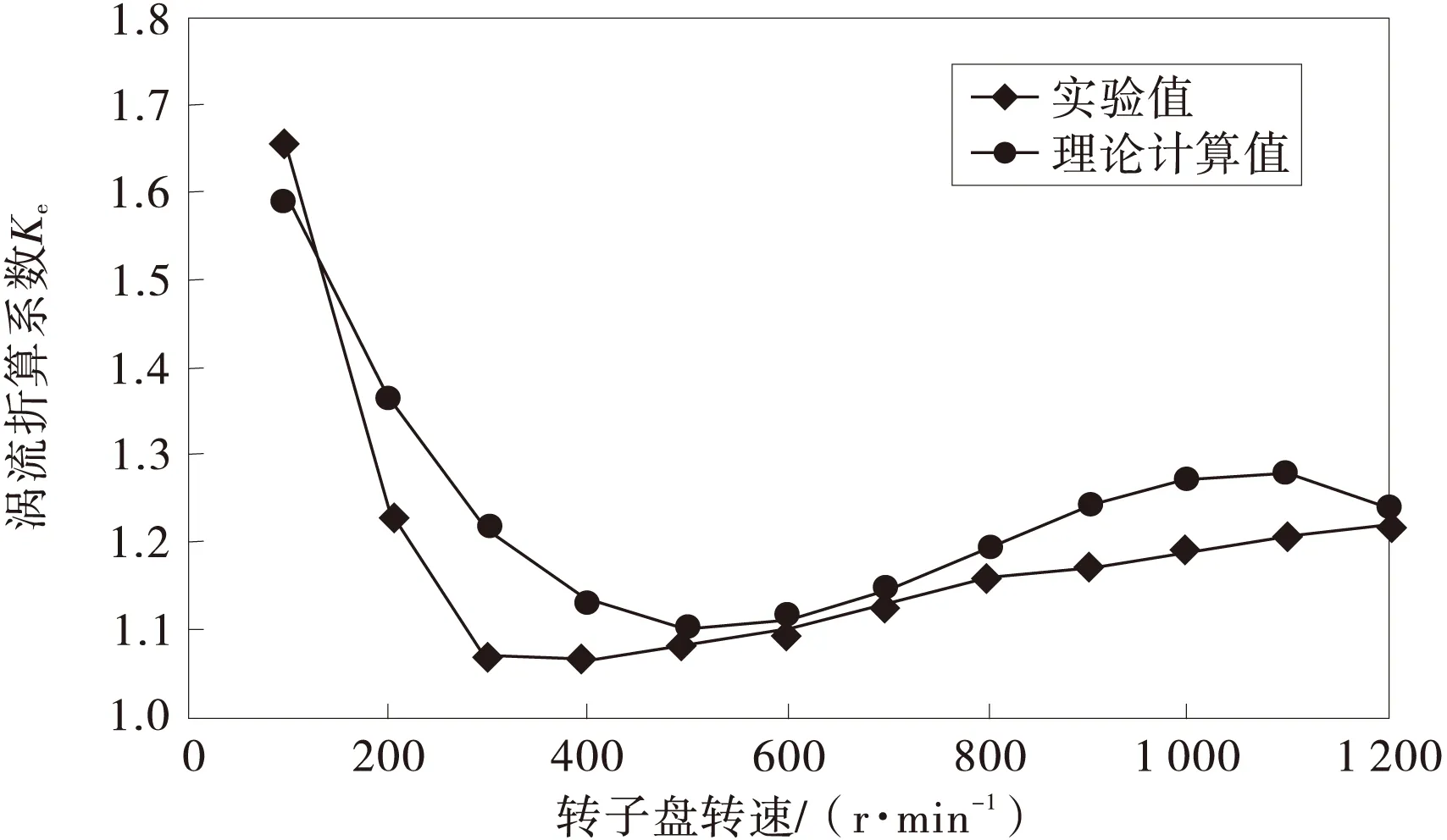
图7 涡流折算系数理论计算值与实验值的曲线

运用龙格-库塔法求解微分方程的数值解，在MATLAB中是利用ode45这个函数，该函数的使用方式是[t,y]=ode45(odefun,tspan,y0,options),其中odefun用于存放待求解微分方程的m文件名，tspan指定自变量的取值范围，y0为函数的边界条件，options设置求解器的相关选项[19]。可以看出要想通过求解微分方程得出涡流折算系数的值，必须知道函数的边界条件y0，即涡流折算系数在转速n=100 r/min的大小。

根据假设2，不同型号电涡流缓速器涡流折算系数对转速的导数大小相同。笔者利用MATLAB遗传算法与直接搜索工具箱[20]得到涡流折算系数在转速n=100 r/min的大小，即y0。

4 计算实例与分析

上文分析涡流折算系数的计算方法时使用了1900型和2200型电涡流缓速器的实验数据，为了证明该方法的正确性，笔者以扬州市洪泉实业有限公司生产的500型电涡流缓速器为例进行计算分析与试验验证。用于计算的500型电涡流缓速器的基本参数如下：转子盘的中心半径为130 mm，磁芯直径70 mm，气隙2.6 mm；8个电磁线圈，构成4组励磁，每个线圈匝数370；外接蓄电池电压为24 V。

笔者首先利用MATLAB遗传算法与直接搜索工具箱中求出y0=1.2，然后利用龙格-库塔法求解得到500型电涡流缓速器的涡流折算系数的曲线如图8。

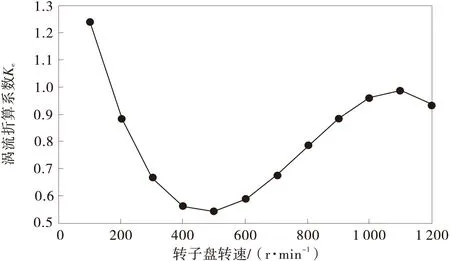
图8 500型电涡流缓速器涡流折算系数的理论计算曲线

利用求得的涡流折算系数数值解，编程计算得到500型电涡流缓速器制动力矩理论值。制动力矩的理论计算曲线与实验所得曲线如图9,可看出基于改进算法的制动力矩的理论计算曲线与实验曲线拟合的很好，而当涡流折算系数Ke=1.2的理论计算结果则与实验值偏差较大，证明笔者提出的涡流折算系数计算方法的实用性。

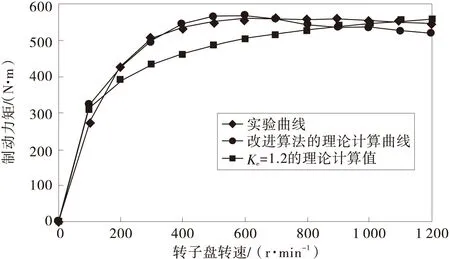
图9 缓速器制动力矩理论计算曲线与实验曲线

5 结 语

笔者在分析涡流折算系数对电涡流缓速器制动力矩理论计算的影响基础上，构造了关于涡流折算系数的微分方程。分析实验结果表明提出的关于涡流折算系数的微分方程可以提高电涡流缓速器制动力矩理论计算值的精度。利用直接搜索工具箱到微分方程的初值条件，再通过龙格-库塔法求解微分方程得到涡流折算系数的数值解，利用这一方法计算涡流折算系数可行有效。关于涡流折算系数计算方法的研究，解决了电涡流缓速器在改型优化和新产品设计中存在的难题。

[1] 何仁.汽车辅助制动装置[M].北京:化学工业出版社,2005. He Ren.Automotive Auxiliary Braking Device [M].Beijing:Chemical Industry Press,2005.

[2] Venkataratnam K,Abdul K.Analysis and performance of eddy- current brakes with ferromagnetic loss drums Part 1:Non-salient-pole- brakes [J].IEE PROC,1982,129(3):125-131.

[3] Venkataratnam K,Abdul K.Analysis and performance of eddy- current brakes with ferromagnetic loss drums Part 2:salient-pole- brakes [J].IEE PROC,1982,129(3):132-142.

[4] Sharifaddin S,Kourosh S.Influence of skin effect on torque of cylindrical eddy current brake [C]//Power Engineering,Energy and Electrical Drives,2009.Lisbon,Portugal:International Conference on IEEE,2009:535-539.

[5] Sharifaddin S,Kourosh S.Performance analysis of a cylindrical eddy current brake [J].Electric Power Applications,IET,2012,6(9):661-668.

[6] 何仁,衣丰艳,何建清.电涡流缓速器制动力矩的计算方法[J].汽车工程,2004,26(2):197-200. He Ren,Yi Fengyan,He Jianqing.A computation method for braking torque of eddy current retarder [J].Automotive Engineering,2004,26 (2):197-200.

[7] 何建清.车用电涡流缓速器的设计方法及其性能分析[D].镇江:江苏大学,2003. He Jianqing.The Design Method of Eddy Current Retarder in Automobile and Its Performance Analysis [D].Zhenjiang:Jiangsu University,2003.

[8] 杨效军,何仁,沈海军.转筒式电涡流缓速器制动力矩计算方法[J].机械科学与技术,2010,29(10):1389-1392. Yang Xiaojun,He Ren,Shen Haijun.A calculation method for the braking torque of a rotary drum eddy current brake [J].Mechanical Science and Technology for Aerospace Engineering,2010,29 (10):1389-1392.

[9] 杨效军,何仁,沈海军.自励式缓速器制动力矩计算方法[J].汽车技术,2009(8):11-14. Yang Xiaojun,He Ren,Shen Haijun.Analytical calculation of braking torque for the self-excited retarder [J].Automobile Technology,2009(8):11-14.

[10] 赵长汉,姜士林.感应加热原理及应用[M].天津:天津科技翻译出版公司,1993. Zhao Changhan,Jiang Shilin.Principle & Application of Elements of Induction Heating [M].Tianjin:Tianjin Science and Technology Translation and Publishing Corporation,1993.

[11] C.B.瓦修京斯基.变压器的理论与计算[M].崔立君,译.北京:机械工业出版社,1983. Baciothhckhiti C B.Theory and Calculation of Transformer [M].Cui Lijun,translation.Beijing:China Machine Press,1983.

[12] 汤蕴璆.电机学[M].北京:机械工业出版社,2011. Tang Yunmiou.Electrical Machines [M].Beijing:China Machine Press,2011.

[13] 汤蕴璆.电机内的电磁场[M].北京:科学出版社,1998.

Tang Yunmiou.Electromagnetic Field within the Motor [M].Beijing:Science Press,1998.

[14] 左俊业,田学义.感应子式涡流测功机的有效参数计算[J].电机技术,1979(2):31-42.0 Zuo Junye,Tian Xueyi.Parameters calculation of induction eddy current dynamometer [J].Electric Machine and Hydraulic Turbine,1979(2):31-42.

[15] 哈尔滨大学电机研究所.涡流测功机[M].哈尔滨:黑龙江科学技术出版社,1983. Institute of Electronics,Harbin University.Eddy Current Dynamometer[M].Harbin:Heilongjiang Science and Technology Press,1983.

[16] 叶乐志.汽车永磁缓速器设计理论与实验研究[D].北京:北京工业大学,2012. Ye Lezhi.Design Theoretical and Experimental Study on Permanent Magnet Retarder for Vehicle [D].Beijing:Beijing University of Technology,2012.

[17] 孙为民,张跃明.电涡流缓速器制动力矩计算的新方法[J].现代机械,2005(4):21-29. Sun Weimin,Zhang Yueming.A new calculation method of brake torque for eddy current retarder [J].Modern Machinery,2005(4):21-29.

[18] 邓长青.城轨车辆涡流制动技术研究[D].成都:西南交通大学,2011. Deng Changqing.Reseach on Eddy Current Braking Technology of Urban Rail Vehicles [D].Chengdu:Southwest Jiaotong University,2011.

[19] 薛定宇,陈阳泉.高等应用数学问题的MATLAB求解[M].北京:清华大学出版社,2004. Xu Dingyu,Chen Yangquan.Higher Applied Mathematics Problem MATLAB Solving [M].Beijing:Tsinghua University Press,2004.

[20] 雷英杰,张善文,李续武,等.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2005. Lei Yingjie,Zhang Shanwen,Li Xuwu,et al.MATLAB Genetic Algorithm Toolbox and its Application [M].Xi’an:Xi’an University of Electronic Science and Technology Press,2005.

Calculation Method of Eddy Current Conversion Coefficients of Eddy Current Retarder

Hu Donghai, He Ren, Tang Bao

(School of Automobile & Traffic Engineering, Jiangsu University, Zhenjiang 212013, Jiangsu, China)

The impact of eddy current conversion coefficient on theoretical calculation of eddy current retarder braking torque was analyzed. Through the analysis of experimental data of braking torque of two different eddy current retarders, differential equation of eddy current conversion coefficient was established. The initial conditions of differential equation were obtained by direct search toolbox of MATLAB, and then the numerical solution of eddy current conversion coefficient was gained by Runge-Kutta method. The braking torque of an eddy current brake was calculated by the derived calculation method. The calculation data accords with the experimental data, and it is indicated that the proposed calculation method is available and can solve the difficult problems of eddy current retarder in modified optimization and new product design.

vehicle engineering; eddy current conversion coefficient; braking torque calculation; Runge-Kutta method; eddy current retarder

10.3969/j.issn.1674-0696.2015.01.31

2013-03-18；

2013-08-04

国家自然科学基金项目(51275212);江苏省2014年度普通高校研究生科研创新计划项目(KYLX-1025)；2013年江苏大学工业中心大学生创新实践基金项目(201302)

胡东海(1989—)，男，江苏镇江人，博士研究生，主要从事汽车机电一体化技术方面的研究。E-mail：jsherohu@163.com。

何 仁(1962—)，男，江苏南京人，教授，博士生导师，主要从事汽车机电一体化技术方面的研究。E-mail：heren@ujs.edu.cn。

U463.212

A

1674-0696(2015)01-144-05