基于多目标优化的水利水电工程评标模型研究

李国兴

(河南省水利第二工程局，河南 郑州 450016)

基于多目标优化的水利水电工程评标模型研究

李国兴

(河南省水利第二工程局，河南 郑州 450016)

通过工程招投标形式选择合适的承包人是水利水电工程项目建设的关键。评标是招标投标工作的重要环节，科学有效的评标方法是正确选择中标单位的关键，关系工程实施的成败。本文基于多目标优化数学模型，选取合适的评价因子，构建工程项目评标模型，能够合理处理各评价因子间相互关联及制约。案例分析表明该方法简单有效，能够为水利水电工程评标工作提供理论参考。

多目标优化；水利水电工程；招标投标；评标模型

1 概 述

招标投标是国内外通用的、科学合理的工程承发包方式，通过招标投标形式选择合适的承包人是工程建设的关键环节，对圆满完成工程建设计划起着决定性的作用[1]。评标是招标投标工作的重要环节，科学合理的评标方法对择优确定中标单位、保护招标投标双方的正当权益及防止招标工作中的违法违规行为均有十分重要的意义[2]。目前我国水利水电工程建设领域普遍采用的评标办法是综合评分法，该方法兼顾了投标报价、施工技术等方面的信息，能够比较客观地反映招标文件的要求[3]。但综合评分法在定性指标定量化的过程中，缺少一种科学合理的转换方法，忽略了各评价因子间的相互关联性[4]。水利水电工程建设是一个复杂的系统，评标的实质是一个集技术、经济、安全、管理等多方面于一体的多目标决策问题，各因素主体间既相互独立又相互关联，确定优选中标单位的过程实际上是一个多目标优化过程。本文以多目标优化理论为基础，选取合适的评价因子，建立基于多目标优化的评标模型，以期为水利水电工程项目建设评标工作提供科学合理的理论指导。

2 评价指标体系建立

2.1 评价指标体系建立的原则

评价指标的选取对评价结果的可靠性有直接影响，水利水电工程项目建设是一个复杂的系统，涉及方面众多，且各因素间相互干扰、相互制约，因而涉及评标的评价因素众多。在选择建立评价指标体系时，应遵循以下原则：ⓐ评价指标应具有代表性，选取的评价指标应能够真实反映工程建设的需要和特点；ⓑ评价指标的相对独立性，每个评价指标应含义明确，相对独立，避免指标间存在相关性造成评价信息重复；ⓒ评价体系的完整性，各评价指标间应相互衔接，共同构成完整的评价指标体系。

2.2 评价指标体系的构建

综合考虑影响水利水电工程建设的主要因素，参考相关文献[5-6]，构建表1所列的评标指标体系。

表1 评价指标体系

上述评价指标体系中，定量指标可直接采用投标文件中的具体数值，定性指标可通过专家打分的方法量化。

3 多目标优化理论

在一个复杂的系统工程中，事件往往存在众多目标，复杂事件往往是多目标问题。多目标问题理想情况下能使所有目标达到最佳的方案，但现实中由于目标间的相互关联和制约性，很难找到能够使所有目标同时达到最优的方案，不得不在非最优方案中优选合适的方案，因而多目标优选问题就转化为了整体择优问题。多目标优化问题的解决需借助理想点法，其思路是将距离理想点最近的解作为多目标的优化解。对于多目标问题的不同量纲，可通过模糊数学中的隶属函数进行度量，并可利用距离特征值进行量化计算，以与理想点距离最接近的解为多目标优化解[7-8]。

3.1 模型构建

设求解的问题有p个目标：

f1(x),f2(x),…,fp(x)

将目标优化(越大越优或越小越优)，可表示为

max或min{f1(x),f2(x),…,fp(x)},X∈D。

若存在X*,使f1(x),f2(x),…,fp(x)达到最优，则称X*为理想点，即

F(X*)=[f1(x),f2(x),…,fp(x)]T

定义非劣解中与理想点最接近的解为多目标问题的优化解。

若有多目标的非劣解为：

F1(x)=[f11(x1),f12(x1),…,f1p(x1)]T

F2(x)=[f21(x2),f22(x2),…,f2p(x2)]T

⋮

Fk(x)=[fk1(xk),fk2(xk),…,fkp(xk)]T

理想点为：

其中fj*可统一表达为：

X=(x1,x2,…，xn)T

使max或minfj(x)约束于qj(x)≤0(j=1,2,…,m)。

从而将非劣解的理想点用最优的隶属函数表征，均以μ(fij)表达，它们在目标论域上的模糊子集为：

理想点的目标值亦可表达为目标论域上的模糊子集：

因此，多目标优化问题可利用模糊数学的方法寻优计算，即最接近F*的解为优化解。

3.2 目标隶属函数

以理想点的目标值为优来表征的隶属函数，通常有定量指标、定性指标两种，此两种指标可分别描述如下[9]：

a.定量指标的目标隶属函数。若目标属性以小为优，即越小越优，则从优隶属函数可表示为：

(1)

式中μij——i方案第j个目标的最优隶属函数；

fij——i方案第j个目标的函数值(也即目标值)；

max(fij)——j目标的最大值；

若目标属性以大为优，即越大越优，则从优隶属函数可表示为：

(2)

式中 min(fij)——j目标的最小值。

b.定性指标的目标隶属函数。定性指标可用模糊评语来表达，可通过赋值将模糊评语量化，从而按定量指标计算隶属函数。

c.目标的权重系数。目标的权重系数表征目标的重要性，权重系数越大，相对重要程度越高；权重系数越小，相对重要程度越低。确定权重系数的方法有很多，常用的有层次分析法、专家打分法、头脑风暴法、熵权等。

3.3 寻求最优解

多目标优化问题可利用模糊数学的模糊性及其度量中的距离概念寻求优化解，通常可以认为与理想点距离最近的非劣解为多目标的优化解。本文采用相对海明(Hammin)距离公式求解优化解。

(3)

4 实例分析

假设以一水利工程项目面向社会公开招标为例，在所有报名的投标单位中有甲、乙、丙、丁四家通过了资格预审。根据四家单位的投标文件内容及建立的评价指标体系，通过专家组审核，确定的各投标单位评价指标值见表2。

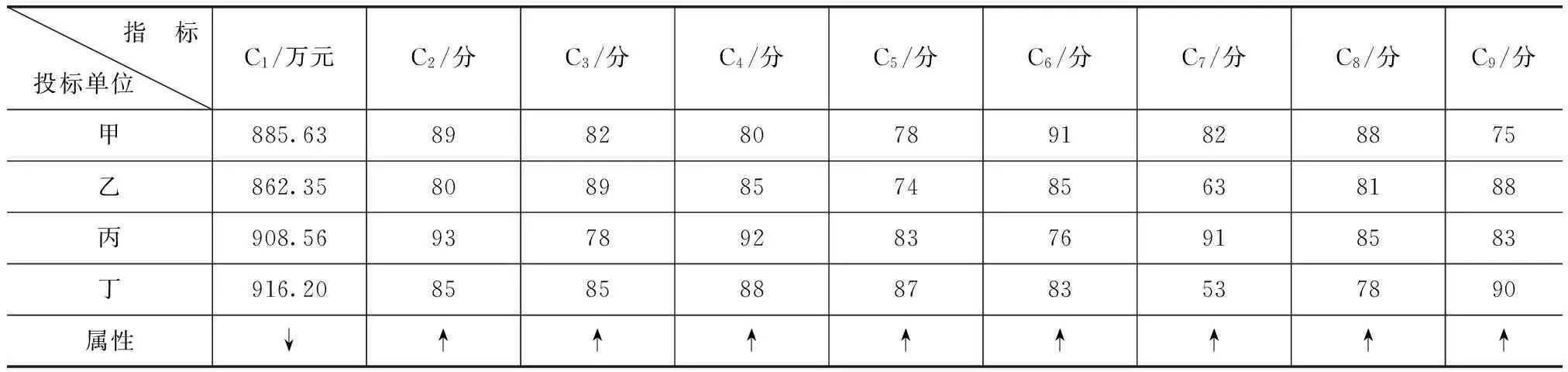
表2 各投标单位的评价指标值

注 表中“↓”表示越小越优，“↑”表示越大越优。定性指标通过专家组赋分量化，分值区间为[0,100]。

4.1 评价指标权重系数的确定

利用层次分析法及专家打分法确定的各评价指标综合权重为：

q=(0.273,0.182,0.091,0.045,0.045,0.227,0.045,0.045,0.045)。

4.2 计算目标隶属函数值

根据式(1)、式(2)分别计算表2中定量及定性指标的隶属函数值。

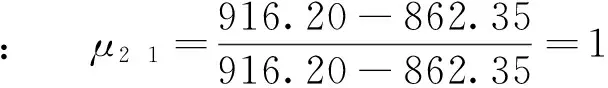
其他目标隶属函数值的求解过程同上。求得的目标隶属函数值见表3。

表3 各投标单位目标隶属函数值

4.3 求解多目标优化解

由式(3)可计算各投标方案的相对海明距离。其中μ(fj*)=1，即为该目标的最优值。

投标单位甲：

同理可求得：

因此可看出丙单位投标内容与理想点距离最近，为最优投标单位。

5 结 语

评标是招标投标工作的重要环节，在水利水电工程项目招标投标过程中，评标方法的优劣直接影响招标投标工作的效果。本文以多目标优化理论为基础，选取合适的评价因子，充分考虑各评价因子间的相互关联和制约性，建立了基于多目标优化的评标模型，能够保证评标的科学合理性，且通过实例分析证明该方法能够快速有效地分析出最优投标人，可为水利水电工程项目评标决策提供理论指导。

[1] 罗文东.水利水电施工组织设计对投标报价的影响[J].水利建设与管理，2013，33(1)：61-63.

[2] 李冲.浅谈工程招投标过程中的评标方法及现状分析[J].科技创新导报，2011(11)：119-119.

[3] 何亚伯，帅青燕.基于复合物元与信息熵的水电工程项目评标模型[J].水电能源科学，2013，31(1)：144-146.

[4] 耿新春.大型水利工程项目投资常见风险和管理要点分析[J].水利建设与管理，2014，34(4)：32-34.

[5] 张国安，王孟钧，李屹.基于多目标优化的无碴轨道铺设施工方案优选[J].科技进步与对策，2009，26(11)：19-21.

[6] 金华征.考虑市场环境的多目标输电网优化规划研究[D].上海：上海交通大学，2007.

[7] 林镇周.论多目标优化在电力工程施工中的应用[J].电力建设，2000(9)：8-10.

Research on water conservancy and hydropower engineering bid evaluation model based on multi-objective optimization

LI Guoxing

(HenanWaterConservancyNo.2EngineeringBureau,Zhengzhou450016,China)

Selection of suitable contractor through project bidding form is critical for construction of water conservancy and hydropower project. Bid evaluation is an important part of the bidding work. Scientific and effective bid evaluation method is critical for correctly selecting bid winning unit, which is related to success of project implementation. In the paper, appropriate evaluation factors are selected based on multi-objective optimization mathematical model for constructing engineering project bid evaluation model. Mutual relations and restriction among various bid evaluation factors can be rationally handled. Case analysis shows that the method is simple and effective, which can provide theory reference for water conservancy and hydropower project bid evaluation works.

multi-objective optimization; water conservancy and hydropower project; bidding and tendering; bid evaluation model

10.16617/j.cnki.11-5543/TK.2015.10.016

TV51

A

1673-8241(2015)10-0053-04