Q235钢板对半球形头弹抗侵彻特性*

邓云飞,孟凡柱,李剑锋,魏 刚

(中国民航大学航空工程学院,天津300300)

Q235钢板对半球形头弹抗侵彻特性*

邓云飞,孟凡柱,李剑锋,魏 刚

(中国民航大学航空工程学院,天津300300)

利用轻气炮进行了半球形头杆弹正撞击单层板和等厚接触式三层板的实验,得到了这两种结构靶体的初始-剩余速度曲线以及弹道极限。采用 ABAQUS/EXPLICIT数值模拟软件对杆弹撞击金属板的过程进行了数值模拟研究,通过对比数值模拟和实验结果,验证了数值模拟材料模型和参数的有效性。研究了靶体结构对抗侵彻特性的影响,并分析了弹体对靶体的撞击过程。研究结果表明:多层板的弹道极限高于等厚单层板。单层板主要失效模式为剪切,而多层板的主要失效模式为整体的蝶形变形和局部的盘式隆起。对于多层板,靶板具体的失效模式与其在靶中位置相关。

爆炸力学;弹道性能;ABAQUS/EXPLICIT;弹体;靶体;弹道极限

近年来,结构撞击问题越发引起关注,除了军事领域中为了应对冲突之外,随着对侵彻和高速撞击问题研究的深入,其应用和关注范围也拓展到了民用的诸多方面。结构撞击的动力学问题依赖于它的应用领域、材料、结构和速度范围等等。防护设计中的一个基本和重要问题就是材料和结构的选取以及优化。由于金属材料在结构防护中是应用最为广泛的材料,所以对其穿甲/侵彻问题的研究特别多。穿甲/侵彻问题的求解往往可以归为3类:(1)实验研究;(2)工程分析模型;(3)数值模拟研究。

I.Marom 等[1]进行了半球形头杆弹 对接触和间隙 式 多 层铝梁撞击实 验,研 究 靶 体 的 抗 侵彻 性 能。通过比较弹体贯穿靶体前后的速度差衡量靶体抗侵彻性能,研究结果表明,分层提高梁的抗侵彻性能,即单层梁的弹道性能低于多层梁,此外间隙式多层梁的弹道性能低于接 触 式 多层梁。 邓云飞等[2]利 用轻气炮进行卵形头、平头以及半球形头杆弹正撞击等厚接触式叠层靶实验,靶体总厚度为2 mm,结果表明:分层结构降低靶体的弹道极限,单层板的抗 侵 彻 性 能高 于 叠 层 板 的 抗侵 彻 性 能。S.Dey 等[3]和T. Børvik等[4]研究了相同厚度不同结构的靶体对直径20 mm平 头 和 卵 形头弹的抗 侵 彻 性 能,靶体包 括 单层靶,接触式和间隙式双层钢靶,靶体总厚度为12 mm。对于平头弹,双层靶的弹道极限高于单层靶,包括接触式和间隙式,而间隙式双层靶的弹道极限低于接触式双层靶的弹道极限。对于卵形头弹,双层靶的弹道极限低于单层靶,包括接触式和间隙式,而间隙对双层靶的弹道极限影响特别小。N.K.Gupta等[5]进行薄铝靶对平头,半球形头和 卵形 头 弹 的 抗 侵 彻特 性 研 究,靶 体包 括 相 同 厚 度 的单 层 靶 和多 层靶。实验证明:双层靶的弹道性能和单层靶接近,但是进一步增加分层数目时,多层靶的弹道极限低于相同总厚度的单层靶。靶体对卵形头弹的弹道极限最低,其次依次为平头弹和半球形头弹。A.Alavi Nia等[6]研究了单层、三层间隙和接触 式 铝靶对半球形 头 弹 的抗侵彻特性,分 析了靶板 厚 度、叠 层顺 序和板间间隙对靶体抗侵彻性能的影响。弹体半径为8.7 mm,质量为12.15 g。单层靶厚度为3 mm,3层靶厚度分别为1.5、1.0和0.5 mm,总间隙为6 mm。研究表明,单层靶的弹道极限高于接触式 和间 隙 式双层靶,并且接触式靶的弹道极限高于间隙式靶。三层靶的弹道极限随第1层和第2层板间间隙的增大而减小。最大弹道极限发生在第1层板最厚,然后依次 是第2层板和 第 3 层板的靶体。郭子涛[7]对Q235钢进行了静态,动态、常温和高温力学性能测试,获取了力学模型,并且验证了模型的有效性。

从研究现状可以发现,相对于数量众多的单层金属防护结构研究,对多层防护结构的研究无论从数量上还是从深度上都比较有限。此外,由于靶体抗侵彻特性涉及到靶板材料、弹体材料、弹体几何形状、靶体几何形状和靶体叠层结构等,影响因素较多,不同的研究者考虑的因素不一样,得到的结论往往不一致,因此目前缺乏比较系统深入地研究。

本文中利用撞击实验和数值仿真研究单层以及等厚多层金属板对半球形弹体的抗侵彻特性,分析靶体结构对失效模式和抗侵彻性能的影响。利用撞击实验结果验证数值模拟计算的有效性,最终采用合适的弹靶数值模型和材料参数对弹靶作用过程进行描述。

1 实验系统方法

撞击实验在一级气炮上进行,该测试设备主要包括:气室;口径12.7 mm,长2 m 的发射管;靶舱;激光测速系统;高速摄像机系统等[8]。

靶体为Q235钢,正方形靶板尺寸为250 mm×250 mm,靶板四周加工有螺栓孔,通过8个 M8螺栓与靶架固定起来,靶板的自由跨度为210 mm×210 mm。单层靶的厚度为6 mm,记为T12。3层2 mm厚钢板叠加为三层靶,靶板间隙为零,记为 T4T4T4。

弹体由经特殊热处理的38CrSi合金钢加工而成,热处理硬度 HRC约为53,直径为12.62 mm,名义质量为34.5 g,弹体头部曲率半径与弹体直径比为0.5,弹体形状及尺寸如图1所示。实验中弹体仅发生非常有限的变形,因此可以认为弹体在侵彻过程中保持刚性,即不发生变形和失效。

图1 弹体形状及尺寸Fig.1 Geometry of the projectiles

2 实验结果及讨论

2.1 侵彻过程

在实验过程中利用高速摄像机追踪侵彻过程,获取撞击侵彻过程的直观图像资料,同时可以获得弹体的速度和加速度等信息。图2给出了弹体贯穿靶体的典型过程。金属弹体在侵彻过程中保持刚性,并且产生圆形帽状冲塞。对比弹体穿甲靶板前后照片,可见弹体的撞击姿态很好。

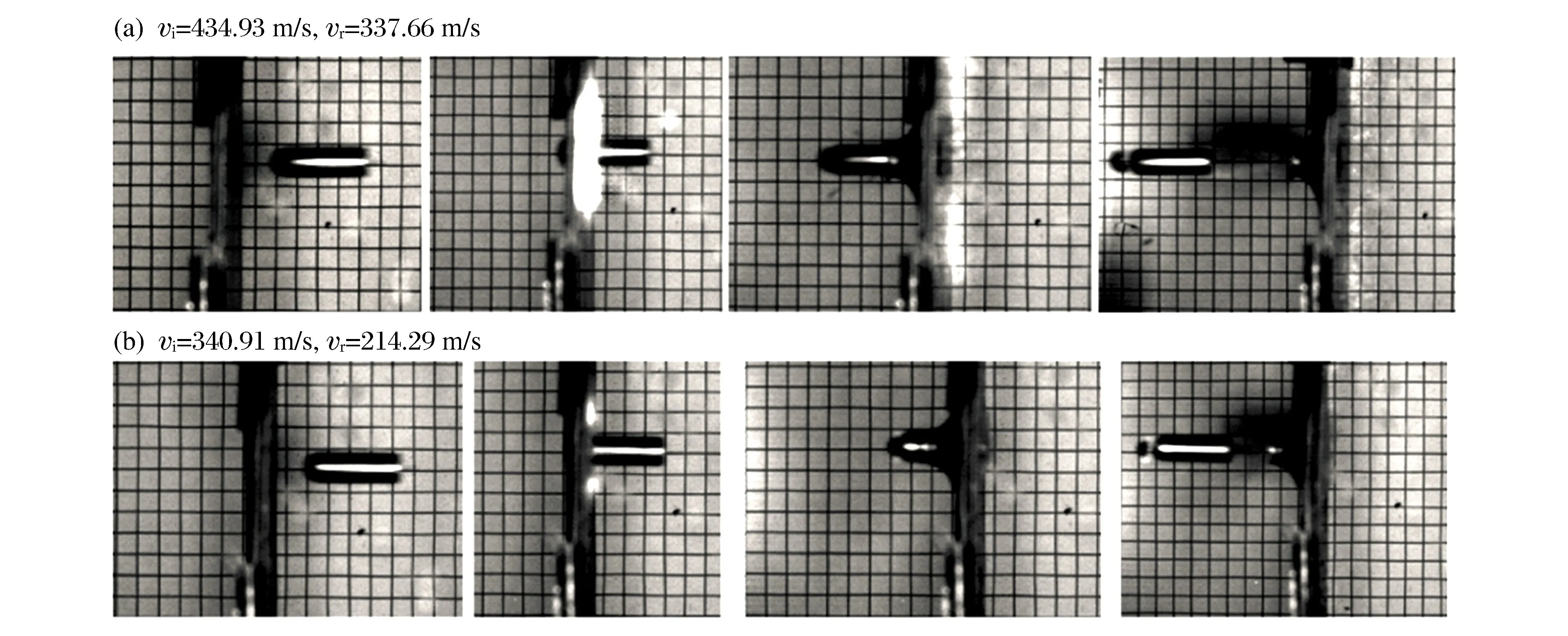
图2 弹体对T4T4T4靶体典型撞击工况Fig.2 Selection of high-speed camera images showing perforation of the T4T4T4 plates

2.2 弹道极限

表1和2给 出 了 撞 击 实 验 得 到 的 初 始 和 剩 余 速 度 数 据,其 中vi和vr分 别 表 示 弹 体 的 初 始 撞 击 速 度和贯穿靶后的剩余速度。

表1 Q235钢靶T12侵彻实验结果Table 1 Penetration test result of the Q235 steel target T12

表2 Q235钢靶T4T4T4侵彻实验结果Table 2 Penetration test result of the Q235 steel target T4T4T4

使用 R.F.Recht等[9]提出的 R-I公式处理弹体的初始-剩余速度关系,并得到靶体的弹道极限

式中 :vbl为 弹 道 极 限 速 度 ;a和p 为 待 定 常 数和分 别 为 子 弹 质 量 和 冲 塞 质量,a和p可以通过对实验获得的弹体初始-剩余速度数据进行最小二乘拟合得到。

图3给出了半球形头弹撞击靶板的实验数据和拟合初始-剩余速度数据曲线,可以发现分层对靶体抗侵彻性能的影响随速度增加而减小,并且多层靶的弹道极限高于单层靶,与文献[2]中薄靶板分层降低靶体的抗侵彻性能的结论相反。这主要涉及到从单层板过渡到多层板,靶板的主要失效模式和耗能方式是否会发生变化。

2.3 失效模型

半球形头弹侵彻 T12靶时,主要失效模式是剪切冲塞,剪切在损伤区域起主要作用,如图4(a)所示。T4T4T4靶的主要失效模式为盘式隆起和蝶形变形,靶板具体失效模式与其在靶中位置相关,如图4(b)和4(c)所示。图 中 No.1,No.2和 No.3 是 把板叠层顺序,分别表示在撞击方向的第1、2和3层板。第1层板产生一个冲塞和形成盘式隆起,类似于延性孔洞扩张;弹孔周围的材料向外扩张,形成延性孔洞扩张;弹孔表面光滑,失效区域内拉伸和弯曲起主要作用,最终发生颈缩失效,产生一个冲塞;这个冲塞和弹体一起继续往前运动并撞击第2层靶,塞块在弹体和第2层板两者的挤压之下在厚度方向变薄而在直径方向变大。第2层板的主要失效模式为蝶形变形,弹孔周围的材料沿撞击方向前扩张,形成严重的盘式隆起,顶部产生裂纹,失效区域内拉伸应力起主要作用,顶部发生开裂;弹孔顶部局部呈现蓝色,这说明发生了大的塑性变形,塑性功使得弹体与靶体接触区域的材料中产生了很高的温升,此处靶体材料发生了氧化;此外,弹孔顶部几乎要形成一个裂纹圆环,事实上这个裂纹圆环本质上为第2层板的冲塞块,由于弹体和第2个冲塞块之间存在相互挤压,弹体在撞击过程中穿过第2个冲塞块和第3层靶体,这在一定程度上增加了靶体的总厚度,将提高靶体的抗侵彻性能,文献[3]中进行了相似的讨论;第3层板仍然主要发生蝶形变形失效,弹孔周围的材料也沿撞击方向扩张,形成特别显著的盘式隆起,顶部发生花瓣开裂。

图5给出了图4(a)和4(b)中靶板的塑 性 变 形曲线,其中:x为 靶 板平面位置,D为位移;对于 T12靶 ,vi=335.66 m/s,vr=224.60 m/s;对 于 T4T4T4 靶 ,vi=340.91 m/s,vr=214.29 m/s。 由 图 5 可 以发现,单层靶的最大变形小于靶板厚度,这说明了靶板整体结构变形小。三层靶中,第3层板的结构变形大于第2层板的结构变形,依次类推。三层靶中靶板的结构变形均大于靶板厚度,并且远远大于单层靶的结构变形,这也说明了在失效区域内是拉伸应力起主要作用。从单层靶过渡到多层靶时,靶体的主要失效模式也从剪切转变到盘式隆起,主要耗能方式从剪切转变到耗能更多的弯曲和拉伸。因此,分层将提高靶体的抗侵彻性能。

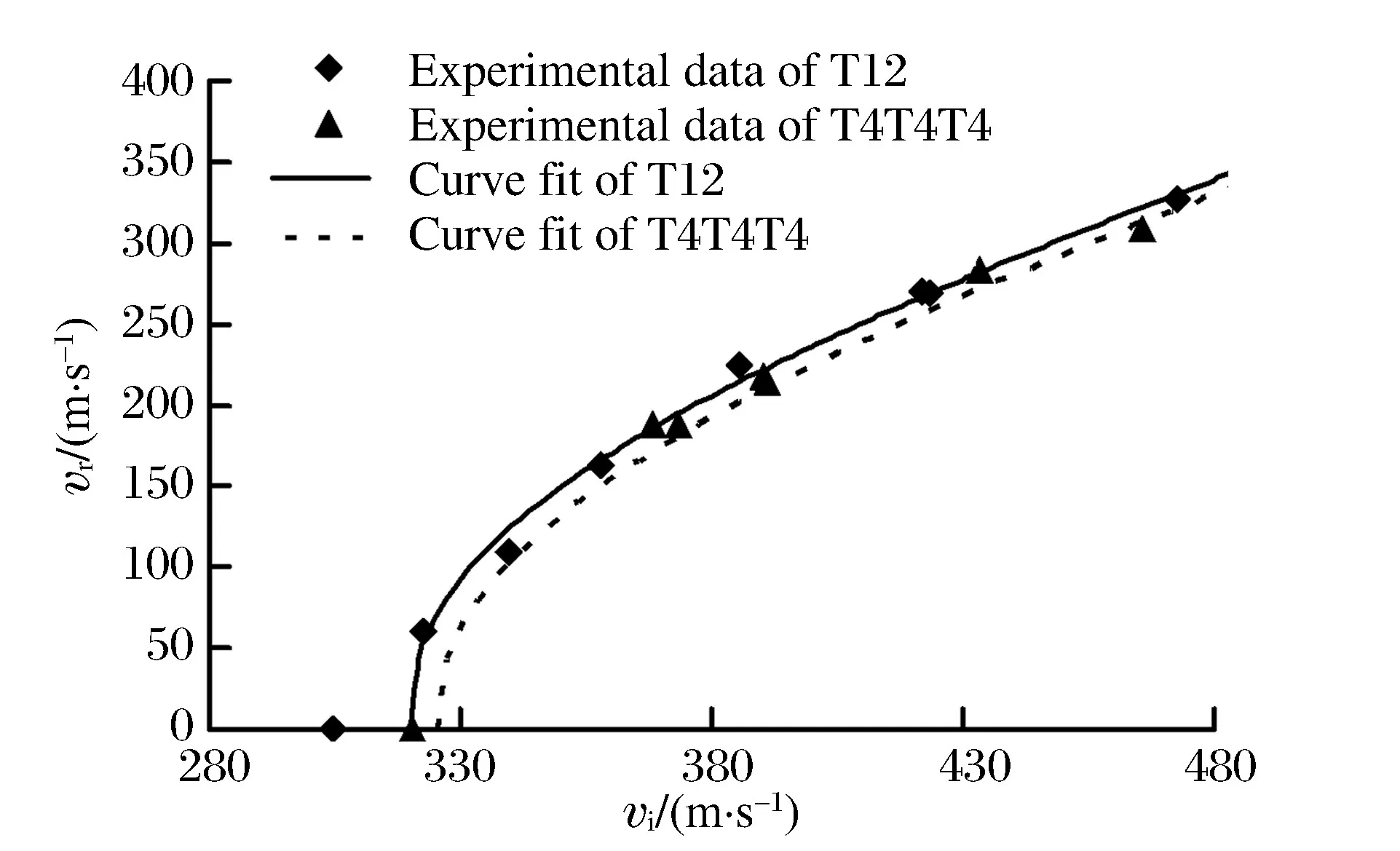
图3 半球形头弹贯穿靶体的初始-剩余速度曲线Fig.3 Residual vs.initial velocity for targets impacted by hemispherical-nosed projectiles

研究发现,Q235钢薄板对半球形头弹撞击,分层将降低靶体的抗侵彻性能。此时,从单层板过渡到多层板,靶板的主要失效模式不发生转变,但是靶板的刚 度 降 低[2]。当 靶 体 的 总 厚 度 超 过 一 定 值 之后,分层将提高靶体的抗侵彻性能,此时,从单层板过渡到多层板,靶板的主要失效模式发生转变,靶板主要失效模式从剪切过渡到盘式隆起和蝶形变形。X.W.Chen 等[10]认 为 靶 板 的 整 体 结 构 变 形 效 应 随靶体厚度和速度增加而减小,但是剪切效应增加,即局部失效效应增加和整体结构变形效应减小。局部失效的耗能效率低于整体结构变形。因此,当多层靶的总厚度大于一定值后其抗侵彻能力高于相同厚度的单层靶,或者说当多层靶的主要失效方式是以拉伸或弯曲而非剪切为主时,抗侵彻能力才增强,说明存在一个临界靶体总厚度。这也与参考文献的结论相一致,文献[5]和[6]中靶体总厚度为3 mm,此时分层降低靶体的抗侵彻性能。但是,文献[1]中靶体总厚度为 5.1~10.0 mm,文献[3]和[4]中 靶 体总厚度为12 mm,此时分层提高靶体的抗侵彻性能。当靶体的总厚度超过临界值后,分层将提高靶体的抗侵彻性能,这个临界值与靶体材料特性及弹体和靶体几何形状等密切相关。

图5 半球形头弹撞击靶板变形线对比Fig.5 Comparison of the deformation profiles of layered plates impacted by hemispherical-nosed projectiles

3 数值模拟

3.1 数值计算模型

数值模拟计算采用有限元软件 ABAQUS/EXPLICIT 6.9的拉格朗日求解器。对 T12建立整体三维模型,为了探讨二维和三维模型的区别,对 T4T4T4建立1/2的整体二维模型,即 Y 轴对称,如图6所示。在数值模拟模型中:靶板简化成直径200 mm 的圆板,四周采用约束固定,即位移为零。靶板自中心采用过渡网格,中心区域网格尺寸为0.25 mm×0.25 mm,离撞击中心区域越远,网格间隔越大。由于弹体在实验中保持刚性,弹体的网格尺寸为1.0 mm×1.0 mm。考虑 到摩擦力对靶体抗侵彻 性 能的影响,弹体和靶体间滑动摩擦因数设为0.1。

图6 靶体的有限元模型Fig.6 Finite element models of the targets and projectiles

在实验中38CrSi弹体仅发生非常有限的变形,由于缺少弹体的材料性质参数,本文中近似认为38CrSi弹体材料与文献[11]中的弹体材料 性 能 相同。文献[11]中弹体使 用 的 为 弹 性 线性 强 化 材料 模型,相关材料参数可从文献[11]中获取。对于 Q235 钢,使 用Johnson-Cook(J-C)强 度 和失 效 模 型,并且对原始J-C 强度模型和失效模型做了修改,模型和参数参考文献[7]。

3.2 数值模拟结果分析

表3给出了实验和采用数值模拟数据依据式(1)拟合得到的模型参数。由实验数据可以发现,多层板的弹道极限高于等厚单层板。

表3 钢靶的弹道极限及模型参数Table 3 Ballistic limit velocityies and model constants of targets

图7给出了实验和模拟得到的初始-剩余速度数据以及由 R-I公式得到的拟合曲线,R-I公式参数见表3。T12数值模拟预测的弹道极限与实验值的误差为5.21%,而 T4T4T4数值模拟预测的弹道极限与实验值的误差为4.95%。由此可以发现实验数据和数值模拟数据之间存在很好的一致性,验证了数值模拟模型和材料参数的有效性,说明数值模拟模型能够很好地描述弹体撞击靶体过程。需要说明的是,实验发现多层靶的弹道极限高于单层靶,并且两者之间相差2.6%,但是数值模拟表明多层靶的弹道极限低于单层靶。此时,单层靶对多层靶的优势被数值模拟的误差所掩盖,主要是因为实验中由于安装方式等因素,靶体不可能到达绝对的固支,只能尽量保证。靶体在弹体撞击过程中存在振动,并且靶板厚度越小,分层数目越多,振动越明显,耗能越多,这将提高靶体的弹道极限。但是,在数值模拟计算过程中,靶体边界被理想的固支,靶体振动可以忽略不计,这将降低靶体的弹道极限,靶体的边界效应对多层靶体弹道的影响高于单层靶体。靶体的弹道极限随其边界的紧固力的增加而减小,R.S.J.Corran等[12]通过实 验研究 对此进 行 了 分 析。 此 外,G.Tiwari等[13]通 过 撞 击 实 验 和 数 值 仿 真 研 究 发 现 单层板的弹道极限随边界的紧固度增加而减小。

图8给出了半球形头弹正撞击 T12靶典型的数值模拟撞击过程图像。由图8可以观察到半球形弹贯穿靶体时发生冲塞破坏。弹体在侵彻靶体过程中,首先挤压剪切靶体,随着侵彻的进行,在弹体前方开始产生微裂纹,裂纹不断扩展,最后冲塞形成并且脱离靶板,弹体穿过靶体,这与实验后观察到的靶体主要失效模式一致。

图9给出了数值模拟半球形头弹正撞击T4T4T4靶典型的撞击过程图像。由图9可以观察到半球形头弹贯穿靶体时发生冲塞破坏,随着叠层顺序在侵彻方向越靠后,靶板结构变形越大。

通过上面的分析,发现数值模拟可以较好地描述半球形头弹对单层靶和多层靶的贯穿物理过程,数值模拟可以给出与实验非常接近的结果,包括弹道极限和初始-剩余速度曲线。

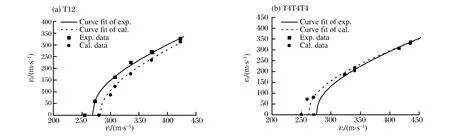
图7 实验结果与数值模拟结果对比Fig.7 Comparisons of the initial vs.residual velocity between experiments and numerical simulations

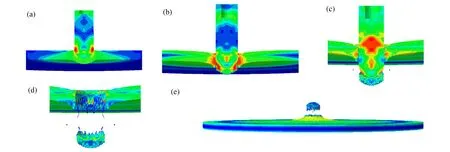
图8 数值模拟得到的半球形头弹贯穿 T12靶图像Fig.8 Perforation pictures of T12 perforated by hemispherical-nosed projectiles for numerical simulations

图9 数值模拟得到的半球形头弹贯穿T4T4T4靶图像Fig.9 Perforation pictures of T4T4T4 perforated by hemispherical-nosed projectiles for numerical simulations

4 结 论

研究了单层金属板和接触式三层金属板对半球形头弹体的抗侵彻性能,分析了靶体结构对靶体抗侵彻性能和失效模式影响。结果表明,采用合适的弹体和靶板材料本构与失效模型能够有效地预测靶板在弹体撞击下的各种失效现象,通过数值模拟获得的结果和实验结果基本一致,包括弹道极限和剩余速度曲线。研究结果表明:多层板的弹道极限高于单层板。单层板的主要失效模式为剪切,而多层板的主要失效模式为整体的蝶形变形和局部的盘式隆起。

[1]Marom I,Bodner S R.Projectile perforation of multi-layered beams[J].International Journal of Mechanical Sciences,1979,21:489-504.

[2]邓 云 飞,张 伟,曹 宗 胜 ,等.分 层 数 对 Q235钢 薄 板 抗 侵 彻 性 能 的 影 响[J].高 压 物 理 学 报,2013,27(4):550-555. Deng Yun-fei,Zhang Wei,Cao Zong-sheng,et al.Influence of the number of layers on the ballistic resistance oflayered thin Q235 steel plates[J].Chinese Journal of High Pressure Physics,2013,27(4):550-555.

[3]Dey S,Bϕrvik T,Teng X,et al.On the ballistic resistance of double-layered steel plates:An experimental and numerical investigation[J].International Journal of Solids and Structures,2007,44(20):6701-6723.

[4]Børvik T,Dey S,Clausen A H.A preliminary study on the perforation resistance of high-strength steel plates[J]. Journal de Physique IV France,2006,134:1053-1059.

[5]Gupta N K,Iqbal M A,Sekhon G S.Effect of projectile nose shape,impact velocity and target thickness on the deformation behavior of layered plates[J].International Journal of Impact Engineering,2008,35(1):37-60.

[6]Alavi Nia A,Hoseini G R.Experimental study of perforation of multi-layered targets by hemispherical-nosed projectiles[J].Material and Design,2011,32(2):1057-1065.

[7]郭子 涛.弹 体入水特性 及不同介质 条件金属靶 的抗侵彻性 能研究[D].哈尔滨:哈 尔滨工业大 学,2012.

[8]邓云飞,张伟,曹宗胜.间隙对 A3钢薄板抗卵形头弹侵彻性能影响的实验研究[J].振动与冲击,2013,32(12):95-99. Deng Yun-fei,Zhang Wei,Cao Zong-sheng.Effect of gap on the ballistic performance of double-layered A3 steel shields against ogival rigid projectiles[J].Journal of Vibration and Shock,2013,32(12):95-99.

[9]Recht R F,Ipson T W.Ballistic perforation dynamics[J].Journal of Applied Mechanics,1963,30(3):384-390.

[10]Chen X W,Li Q M.Shear plugging and perforation of ductile circular plates struck by a blunt projectile[J].International Journal of Impact Engineering,2003,28(5):513-536.

[11]Dey S,Børvik T,Teng X,et al.On the ballistic resistance of double-layered steel plates:An experimental and numerical investigation[J].International Journal of Solids and Structures,2007,44(20):6701-6723.

[12]Corran R S J,Shadbolt P J,Ruiz C.Impact loading of plates:An experimental investigation[J].International Journal of Impact Engineering,1983,1(1):3-22.

[13]Tiwari G,Iqbal M A,Gupta P K,et al.The ballistic resistance of thin aluminium plates with varying degrees of fixity along the circumference[J].International Journal of Impact Engineering,2014,74:46-56.

The ballistic performance of Q235 metal plates subjected to impact by hemispherically-nosed projectiles

Deng Yun-fei,Meng Fan-zhu,Li Jian-feng,Wei Gang
(College of aeronautical Engineering,Civil Aviation University of China,Tianjin 300300,China)

Monolithic and three-layered plates were normally impacted by hemispherically-nosed projectiles.The residual velocity-the initial velocity curves of the projectiles and ballisitic limit velocities were constructed.The penetration process of metal plates impacted by rod projectiles has been studied with numerical simulation code ABAQUS/EXPLICIT.The validation of models and parameters of materials has been proved by comparing the experiment results with numerical simulations.We investigated the influence of combination configuration of target on the ballistic characteristic,including the ballistic resistance and failure models.Furthermore,the impact process was also analyzed.The results indicated that the ballistic limit velocity of multi-layered plate was higher than that of monolithic plate.The dominant failure model of monolithic plate was shearing,but the dominant failure models of multi-layered plate were global dishing and local bulging.Moreover,the failure models of plates of multi-layered plates were in relation to their order in targets.

mechanics of explosion;ballistic performance;ABAQUS/EXPLICIT;projectile;target; ballistic limit

O381国标学科代码:13035

:A

10.11883/1001-1455(2015)03-0386-07

(责任编辑 王小飞)

2013-11-29;

2014-03-30

国 家自然科学 基金项目(11072072);中央高校基 本科研业务 费资助项目(3122014D018);中国民航大学研究生科技创新基金项目(Y15-04)

邓云 飞(1982- ),男,博士,讲师,dengyunfei@eyou.com。