含水层中重金属溶质运移动力学模型研究进展

陶 安,刘曙光,娄 厦,代朝猛

(同济大学土木工程学院,上海 200092)



含水层中重金属溶质运移动力学模型研究进展

陶 安,刘曙光,娄 厦,代朝猛

(同济大学土木工程学院,上海 200092)

在总结国内外重金属污染研究的基础上,综述含水层中重金属溶质运移动力学模型的发展,归纳总结模型的计算方法。讨论了模型参数的确定方法,以及温度,pH值,孔隙水流速,有机质与胶体,土壤非均匀性对参数确定的影响。最后,指出含水层中重金属溶质运移过程中目前研究存在的主要问题,并对将来在该领域需重点研究的内容进行展望。

地下水;含水层;重金属运移;数值模拟;动力学模型;土壤非均匀性

由于地表水容易受到自然条件和人为因素的影响,地下水已经逐渐成为城市供水的主要水源。重金属溶质以其不可降解性和生物积累性等特点成为威胁地下水资源的主要污染物之一。研究表明,我国地下水中80%的浅层地下水和30%的深层地下水已不同程度地受到了重金属污染,其中最主要的重金属污染物为汞、镉、铬和铅[1]。根据《全国地下水污染防治规划(2011—2020年)》,近十几年中我国地下水重金属污染呈现由点到面、由浅到深、由城市向农村蔓延的趋势,污染程度日益严重。重金属污染已成为我国地下水污染控制的重中之重,研究重金属溶质在地下水含水层中的运移规律也受到了众多研究人员的高度关注。

重金属溶质在含水层中的运移受到对流、水动力弥散、吸附解吸和氧化还原等多种复杂作用的影响[2-3]。应用数学模型模拟重金属溶质在含水层中的运移可以预测地下水中重金属污染的瞬时情况和污染物的扩展范围。数学模型可分为确定型模型和随机型模型。确定型模型描述含水层中污染物的运移是以1961年Nielsen等[4-5]提出的对流弥散方程为基础的,根据确定的参数及边界条件可求得确定型模型的解。随机型模型是从研究含水层非均质性及其尺度效应开始的,依赖于多孔介质性质变异的随机函数变量[6]。本文综述含水层中重金属溶质运移动力学模型的发展,并根据国内外的相关研究总结模型的计算方法。在此基础上,进一步讨论模型参数的确定方法及影响参数确定的因素。最后,作者针对目前含水层中重金属溶质运移研究过程中存在的主要问题进行探讨。

1 重金属溶质运移动力学模型的发展

1.1 确定型模型

达西定律自提出以来,由于其形式简单,一直被认为是地下水动力学中最为基本的定律，地下水流动基本微分方程、裘布依稳定井流模型等都是基于其发展的。但达西定律提出后的很长时间里,国内外学者对地下水研究都未考虑溶质运移问题。1952年Lpaidus和Amundson首次将一个类似于“对流-扩散”方程的数学模型应用于溶质运移问题[7]。1960年Nielsen等[4-5]基于质量守恒推导了“对流-弥散”方程(CDE),其一般形式见式(1)所示。此后,该方程一直是研究多孔介质中溶质运移的经典方程和基本方程[8]。

(1)

式中:θ为土壤体积含水量,%;c为溶质质量浓度,mg/L;ρ为土壤干容重,g/cm3;S为溶质在土壤上的吸附量,%;D(θ,v)ij为水动力弥散系数,cm2/min;v为对流速度,cm/min;qi为土壤水流通量,cm/min;t为时间,min;xi为空间坐标,x1,x2,x3分别代表x,y,z;φk为源项,包括生物吸收、化学反应、降解、沉淀等过程,对于重金属溶质来说,可以忽略其降解项。

式(1)中左边第2项求解是很难的,为了便于研究,一般进行转化,见式(2)所示。

(2)

(3)

式中:Kd为分配系数,L/g;λ为源项系数。

本文引入了描述污染物吸附解吸作用的1个重要参数,即阻滞系数Rd,其表达式见式(4)。

(4)

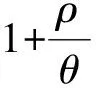
此后,国外学者Beyer等[10]基于实测土壤属性和镉离子的土柱淋溶实验,建立了德国诺尔登哈姆地区地下水中镉离子运移的对流-弥散方程。钱天伟等[11]认为,使用吸附等温线的概念并不能解释“固-液”界面所发生复杂物理化学反应的内在规律。他利用表面络合吸附理论研究了地下水中“固-液”表面的溶质分布特征,并将其与传统的“对流-弥散”模型相耦合,建立了一个能够考虑表面络合吸附影响的溶质运移模型,模型模拟结果与实际值吻合得较好。

对于非均质含水层中的溶质运移,很多情况下会出现反常扩散,因此无法应用传统对流-弥散理论对其进行描述。许多学者开始质疑传统“对流-弥散”模型所基于的理想假设给现实含水层溶质运移问题的描述和模拟带来了不可避免的误差和缺陷[12]。近年来,对传统二阶“对流-弥散”方程进行改进的主流方法之一就是分别对时间或空间进行分数微分,进而依据非线性函数的关联方程描述相应的弥散系数。常福宣等[13]对弥散过程考虑时间和空间相关性,用非局域处理法,推导出对时间和空间分数阶微分的“对流-弥散”方程,见式(5)所示。

(5)

Xia等[14]通过对非均匀含水层中的反常扩散数值试验进一步说明了分数阶“对流-弥散”方程在研究含水层污染物运移中的重要意义。

传统“对流-弥散”模型能很好地体现出含水层中溶质运移的过程机理,其参数也具有明确的物理意义,故目前的应用以确定型模型为主。但由于地下水运动中的不确定性因素较多,包括含水层介质的物理化学特性以及溶质运移过程和运动参数等,模型中参数随时空的变异性会产生尺度效应问题[15]。即使是改进的分数阶“对流-弥散”方程,在模拟较长距离的污染物运移时,仍会出现尺度效应。因此,对于确定型模型在不同的模拟尺度下如何消除或减少尺度效应是一个需要研究的问题。

1.2 随机型模型

近几十年来,随机理论迅速地应用于地下水污染物的运移研究中。随机型模型依赖于含水层性质变异的随机函数变量,引入含水层空间随机场的概念,在理论上将污染物的宏观弥散与含水层介质的统计特征相联系,从而解决了宏观弥散系数的求解问题[16]。Acar等[17]提出了估计一个地下水和污染物排放量的随机模型,并用蒙特卡罗方法估计了参数不确定性。Coppola等[18]应用随机方法研究了介质垂向非均匀性对于溶质运移的影响。

对于随机型模型,非均匀含水层统计参数的方法、模型的理论完善及野外试验验证方面仍需要进一步的研究。目前许多研究者都很重视随机理论和随机型模型的应用研究,虽然其仍处于发展的初期,距离实际应用还有一定距离,但它仍然是一种比较有应用前景的理论模型。

2 模型的计算方法

2.1 确定型模型计算方法

除了在条件比较简单、理想的情况下可求得解析解外,数值方法是解决地下水污染实际问题最常用的方法。数值方法可归纳为3类方法,即欧拉方法、拉格朗日方法以及二者的混合方法。目前,欧拉方法应用较多,而拉格朗日方法和欧拉-拉格朗日方法还只停留在研究阶段,在实际中应用较少[16]。欧拉方法主要包括有限差分法、有限元法、有限体积法和边界元法等。国内外学者的研究情况如表1所示。

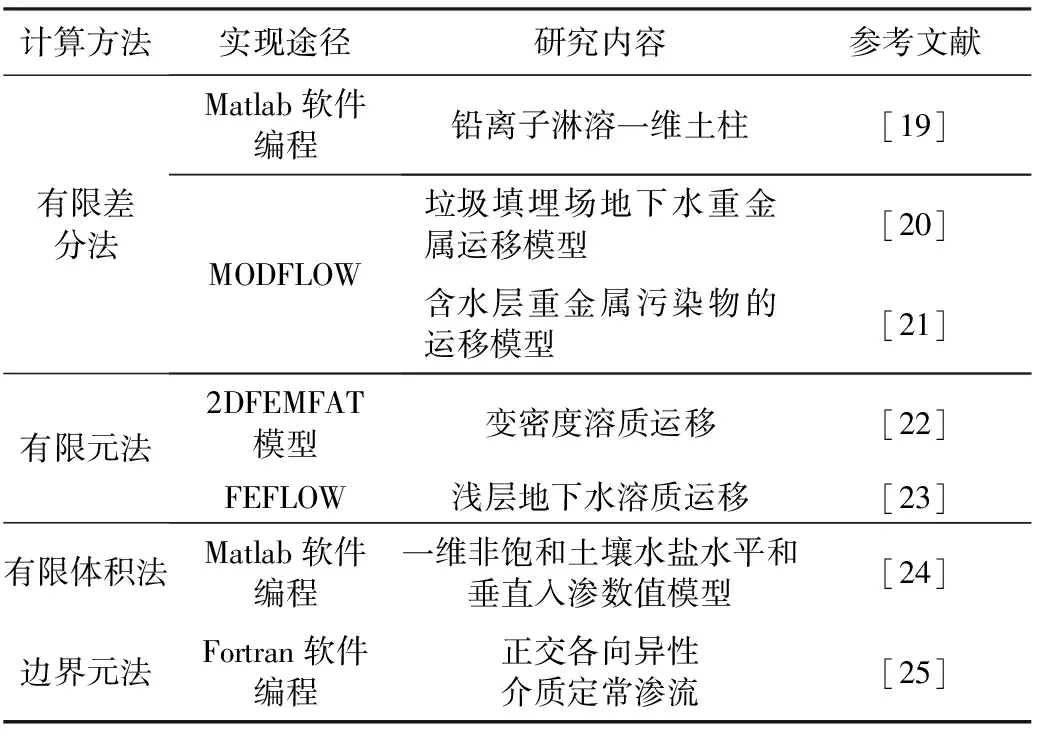
表1 确定型模型欧拉求解方法

2.2 随机型模型计算方法

地下水随机型模型计算方法主要有矩方程法、摄动待定系数法和蒙特·卡罗法[26]。矩方程方法是通过求解有关均值和协方差的随机偏微分方程获得随机问题的解;摄动待定系数法是把随机变量表示为确定性部分和由摄动引起的随机部分;蒙特·卡罗法则是通过平均一系列反映含水层实际性质的确定性问题来模拟随机过程的一种计算机模拟方法[16]。

经过十几年的发展,近年来国内外不少学者提出了自己关于模型计算和建模理念方面的新见解。Mazzia等[27]提出了一种新的求解高盐分在地下水中运移动力学二维非线性方程的数值方法。该方法对时间和空间采用了不同的差分格式,保证了流速场和浓度场预测的高精度性和高稳定性。王浩然等[28]利用区域分解法建立了王旺庄水源地地下水的边界单元法(BEM)与有限单元法(FEM)耦合模型,在需要重点研究的地段采用有限单元法处理,而非重点研究的外围地区则采用边界单元法解决。O’Malley等[29]综合了考虑地球化学反应、对流、弥散及其他微尺度作用,利用概率论方法求解了反常扩散大尺度随机型模型的解析解,并对参数的不确定性进行了分析。

3 模型参数的确定方法及其影响因素

3.1 模型参数的确定方法

在动力学模型的建立过程中,参数确定的准确性研究是很重要的,是污染物在含水层中运移转化模拟计算的关键问题。

水动力弥散系数是最主要的运移参数,主要通过控制弥散过程来影响运移,但其测定具有较大难度,且一直存在较多争议[30]。国内外测定含水层中水动力弥散系数的计算方法主要有公式法、穿透曲线法和水平土柱吸渗法、垂直土柱吸渗法、极大似然法、瞬时剖面法、水分特征曲线法和反函数法等[31-32]。水动力弥散系数的测定方法及国内外学者的研究情况如表2所示。

阻滞系数是用来表示含水层介质对溶质运移阻滞能力的物理化学参数,可以采用室内试验或野外试验方法进行确定。野外试验成本大,耗时长,且重金属溶质会造成污染,因此国内外都倾向于通过室内试验方式获得阻滞系数。室内测定阻滞系数主要方法有动态柱法和批式法。通常情况下,批式法得出的阻滞系数值要比动态柱法的结果大得多。相比之下,动态柱法更接近野外实际情况,但动态柱法实验周期太长[41]。

3.2 模型参数的影响因素

含水层中重金属溶质运移转化动力学模型的参数受多种条件的影响,因此,在确定模型参数时必须综合考虑温度、pH值、孔隙水流速、有机质与胶体和土壤非均匀性等因素的影响。

表2 水动力弥散系数测定方法

3.2.1 温度

温度的改变会影响离子运动的剧烈程度。Medina[42]等研究认为在恒定压强下,弥散系数随着温度的增加而增大,但随着压强的增大,弥散系数受温度的影响减小。Do[43]研究了不同温度对于Zn、Cd离子在黏土含水层中运移的影响。研究表明,温度从15℃上升到55℃,两种重金属离子的弥散系数都会增大,多达10倍。温度对于阻滞系数的影响是基于重金属离子的吸附机理,Cd主要以离子态存在,阻滞系数受温度影响变化小;Zn主要以碳酸盐相存在,阻滞系数随温度增加而增加,多达2倍。因此,在温度从15℃上升到55℃时,含水层中Cd离子的弥散锋从7 mm处扩大到了15 mm处,而Zn离子的弥散锋几乎不变。

3.2.2 pH值

pH值反映的是地下水中的H+浓度,H+浓度会对重金属离子与含水层介质发生的络合作用产生影响。Moradkhani等[44]通过试验研究发现,Zn、Cd和Mn 3种重金属离子的最大分解百分比随着pH值的增大而减小。Chotpantarat等[45]对4种重金属离子溶液在pH值分别为4和5的条件下进行淋溶试验,研究表明,在溶液pH值为5时,由于H+浓度的减小,重金属离子的阻滞系数较溶液pH值为4时大。pH值所产生的不同运移效果可能有以下原因:pH值较低时,以静电吸附为主,H+浓度达到破坏含水层介质表面官能团与重金属的络合,使吸附态重金属离子全部交换解吸下来;随pH值升高,含水层介质表面含氧基团得到活化,更多的重金属离子被络合,不易解吸下来;当pH值超过一定值后,会产生沉淀反应,也导致解吸量急剧减少[46]。

3.2.3 孔隙水流速

含水层中孔隙水流速会随时间和空间变化,但在求解溶质运移方程时通常忽略其对水动力弥散系数的影响。Bond[47]求解了考虑孔隙水流速对水动力弥散系数影响的非饱和非稳定流的水动力弥散方程,研究结果表明,考虑孔隙水流速的影响会使弥散宽度在短时间内增大很多。Pang等[48]通过均一压实消除物理非平衡影响的土柱进行孔隙水流速对于Cd、Zn、Pb离子运移影响的实验,结果表明,分配系数与孔隙水流速呈正相关,阻滞系数与孔隙水流速呈负相关,这说明低流速使重金属离子与介质接触得充分,利于吸附达到动态平衡,因而吸附量较大。

3.2.4 有机质与胶体

含水层中的有机质是一个不均匀的混合体,由于有机质具有较多的含氧官能团(羧基、酚基、羟基等),重金属与有机物质之间有很强的亲和性。章明奎等[49]用室内分析方法研究了土壤颗粒状有机质(POM)对Cu、Cd、Co、Pb、Ni和Zn等6种常见重金属离子的吸附作用。研究表明,土壤中颗粒状有机质对重金属离子有较高的吸附能力,吸附过程是一个快速反应,在100 min内可接近平衡。余贵芬等[50]对含水层中镉的有效性研究发现,有机质对含水层中重金属的离子活性有很大的影响,有机质的分子量、组分和环境条件均会对镉的移动性和生物活性造成影响。胶体是指粒径范围在1 nm～10 μm之间的能起到污染物载体作用的颗粒物,包括层状硅酸盐、铁铝三氧化物、有机大分子等[51-52],在土壤中普遍存在。胶体与含水层中污染物的相互作用是一个极为复杂的微观过程[53-55]。Saiers等[56]进行了铯离子和无机胶体的协同运移室内实验,结果表明减小孔隙水离子强度可以使无机胶体促进铯离子的运移。Baumann等[57]通过对垃圾填埋场的现场试验研究发现,胶体会从垃圾填埋场与含水层的交界面渗出,并形成一层致密层。此致密层减小了交界面的水力渗透系数,也增加了含水层介质对重金属离子的吸附能力。

3.2.5 土壤非均匀性

室内测定水动力弥散系数一般是在均匀土中进行的,然而现实的土壤却是非均匀的。土壤的非均匀性会导致水流在含水层中流向流速等发生变化,进而影响水动力弥散系数。尚熳廷等[58]以Br-作示踪剂,通过室内实验测定含大孔隙的原状土和均质扰动土的水动力弥散系数和弥散度。结果表明,大孔隙的存在使原状土水动力弥散系数比扰动土大2个数量级。土壤的非均匀性和空间变异性导致了渗透系数存在尺度效应,而渗透性能的变异性直接影响到含水层中溶质的运移过程[59]。李国敏等[60]认为产生尺度效应主要原因就是含水层介质具有非均质性,他通过解析方法和数值模型求出了尺度效应的分维数,结果表明数值模型所得出的纵向弥散度随研究尺度增加而增大的速度小于用解析模型所求出的相应值。王永森等[61]通过现场观测数据应用浓度方程进行了观测井弥散系数的反求,应用分维理论确定了弥散系数尺度效应的分维数为1.82567,即弥散系数与尺度之间呈幂相关关系。

4 结论与展望

基于以上对含水层中重金属溶质运移动力学模型研究进展的评述,今后该领域的研究应重点关注以下几个方面:

a.重金属污染物在地下水系统运移的整体性研究。重金属污染物一般是先通过非饱和带再进入地下水,如垃圾填埋场渗漏的重金属污染物等。由于非饱和带的特殊性,水流在非饱和带的运动与饱和带不同,溶质运移过程则更为复杂。然而以往的研究主要是对非饱和带与饱和带进行独立研究,缺少符合实际情况的整体性研究,未来在该方向应作深入的探索。

b.含水层的空隙。对于一般的含水层,空隙很小,地下水流速缓慢,均符合达西渗流定律。而当含水层介质中出现较大裂隙甚至是空洞时,地下水流速会变得很大,此时达西定律不再适用,如喀斯特溶洞、宽大的构造裂隙等。此时溶解于地下水中的重金属溶质随着地下水的流动而快速运移,造成的危害也更大。目前,国内外对于此问题尚处在探索阶段,机理研究、数值模拟方法等方面有待进一步发展。

c.模型参数的确定及尺度效应。重金属溶质的运移参数受到多方面的影响。如重金属离子的吸附与解吸,不仅与含水层介质的粒径有关,还与原先吸附在介质表面的重金属离子种类、浓度和价位有关。这是一个复杂的物理化学微观过程,而目前的数学模型对于该过程的研究极为薄弱。因此今后的研究应加强学科间交叉,宏观结合微观来探索重金属溶质在含水层中的运移。此外,模型在不同的模拟尺度下如何消除或较少尺度效应有待于进一步探索。

d.边界条件的研究。随着全球温室效应的加剧,极端天气事件频出。暴雨、干旱等通过影响含水层中流场的变化来影响重金属的运移规律。另外,在沿海地区,复杂水动力条件如波浪、潮汐和风暴潮等,均会影响近岸含水层中重金属的运移,进而威胁到海岸带资源与生态环境。然而,国内外对于这些方面的研究甚少。

含水层中重金属溶质运移动力学模型是在考虑主要影响因素的前提下对实际过程进行一定简化的理论研究。实际过程非常复杂,某些因素的不当简化往往会造成模拟结果与实际过程的较大偏差,因此对该过程的研究还有待进一步的探索和细化。

[1] 王焰新.地下水污染与防治[M].北京:高等教育出版社,2007:7-10.

[2] CETIN B,AYDILEK A H,LI L.Experimental and numerical analysis of metal leaching from fly ash-amended highway bases[J].Waste Management,2012,32(5):965-978.

[3] KESKIN T E,TOPTAS S.Heavy metal pollution in the surrounding ore deposits and mining activity:a case study from Koyulhisar (Sivas-Turkey)[J].Environmental Earth Sciences,2012,67(3):859-866.

[4] NIELSEN D,BIGGAR J.Miscible displacement in soils:I.experimental information[J].Soil Science Society of America Journal,1961,25(1):1-5.

[5] NIELSEN D,BIGGAR J.Miscible displacement:III.theoretical considerations[J].Soil Science Society of America Journal,1962,26(3):216-221.

[6] FETTER C W,FETTER J C.Contaminant hydrogeology[M].New Jersey:Prentice Hall New Jersey,1999:73-80.

[7] OBERDORFER J A.Hydrogeologic modeling of submarine groundwater discharge:Comparison to other quantita-tive methods[J].Biogeochemistry,2003,66:159-169.

[8] 孙讷正.地下水污染:数学模型和数值方法[M].北京:地质出版社,1989:38-50.

[9] ROWE R K,BOOKER J R.A finite layer technique for modeling complex landfill history[J].Canadian Geotechnical Journal,1995,32(4):660-676.

[10] BEYER C,ALTFELDER S,DUIJNISVELD W H M,et al.Modelling spatial variability and uncertainty of cadmium leaching to groundwater in an urban region[J].Journal of Hydrology,2009,369(3/4):274-283.

[11] 钱天伟,陈繁荣,武贵斌,等.一种耦合表面络合吸附作用的地下水溶质迁移模型初探[J].辐射防护通讯.2003 (3):14-18.(QIAN Tianwei,CHEN Fanrong,WU Guibin,et al.An initial research on solute migration model coupled with adsorption of surface complexation in groundwater[J].Radiation Protection Bulletin,2003(3):14-18.(in Chinese))

[12] 覃荣高,曹广祝,仵彦卿.非均质含水层中渗流与溶质运移研究进展[J].地球科学进展.2014(1):30-41.(QIN Ronggao,CAO Guangzhu,WU Yanqing.Review of the study of groundwater flow and solute transport in heterogeneous aquifer[J].Advances in Earth Science,2014 (1):30-41.(in Chinese))

[13] 常福宣,吴吉春,薛禹群,等.考虑时空相关的分数阶对流-弥散方程及其解[J].水动力学研究与进展:A辑，2005(2):233-240.(CHANG Fuxuan,WU Jichun,XUE Yuqun,et al.The fractional order advection-dispersion equation withtemporal and spatial correlation and its solution[J].Journal of Hydrodynamics,2005(2):233-240.(in Chinese))

[14] XIA Y,WU Jichun.Numerical simulation of fractional advection-diffusion equation:a method to anomalous diffusion[C]//Calibration and Reliability in Groundwater Modeling:Managing Groundwater and the Environment.Wuhan:China Univ Geosciences Press,2009:433-436.

[15] 陈崇希,李国敏.地下水溶质运移理论及模型[M].武汉:中国地质大学出版社,1996:26-32.

[16] 王俊,张津涛,王莉静.地下水污染数学模型综述[J].天津城市建设学院学报,2006(4):273-277.(WANG Jun,ZHANG Jintao,WANG Lijing.Development of mathematic model of groundwater pollution[J].Journal of Tianjin Institute of Urban Construction,2006(4):273-277.(in Chinese))

[17] ACAR O,KLAMMLER H,HATFIELD K,et al.A stochastic model for estimating groundwater and contaminant discharges from fractured rock passive flux meter measurements[J].Water Resources Research,2013,49(3):1277-1291.

[18] COPPOLA A,COMEGNA A,DRAGONETTI G,et al.A stochastic texture-based approach for evaluating solute travel times to groundwater at regional scale by coupling GIS and transfer function[C]//Four decades of progress in monitoring and modeling of processes in the soil-plant-atmosphere system:Applications and challenges.Naples:Procedia Enuironmental Sciences,2013,19:711-722.

[19] 张洋.重金属污染物在多孔介质中的迁移模型与仿真[D].重庆:重庆大学,2012.

[20] TANTEMSAPYA N,NAKSAKUL Y,WIROJANAGUD W.Mathematical modeling of heavy metals contamination from MSW landfill site in Khon Kaen,Thailand[J].Water Science and Technology,2011,64(9):1835-1842.

[21] GALITSKAYA I,POZDNIAKOVA I,TOMS L.Simulation of contaminant transport for contamination risk assessment[C]//Calibration and reliability in groundwater modeling:managing groundwater and the environment.Wuhan:IAHS Publication,2011:172-178.

[22] ZHANG Q,VOLKER R,LOCKINGTON D.Influence of seaward boundary condition on contaminant transport in unconfined coastal aquifers[J].Journal of contaminant hydrology,2001,49(3):201-215.

[23] 孙志浩,王开章.济宁市湖东平原浅层地下水溶质运移数值模拟[J].人民黄河.2010,32(4):83-84.(SUN Zhihao,WANG Kaizhang.Numerical simulation of shallow groundwater solute transportin Jining koto plain[J].Yellow River,2010,32(4):83-84.(in Chinese))

[24] 吕岁菊.有限体积法在土壤水-盐运动规律数值模拟中的应用[D].银川:宁夏大学,2005.

[25] 田玲玲.直接边界元法及其在地下水渗流问题中的应用[J].西华大学学报:自然科学版.2006,25(1):44-45.(TIAN Lingling.Boundary element method and its applicationin seepage of groundwater problem[J].Journal of Xihua University:Natural Science,2006,25(1):44-45.(in Chinese))

[26] 金忠.多孔介质中水分及溶质运移的随机理论[M].北京:科学出版社,2000:104-118.

[27] MAZZIA A,PUTTI M.Mixed-finite element and finite volume discretization for heavy brine simulations in groundwater[J].Journal of Computational and Applied Mathematics,2002,147(1):191-213.

[28] 王浩然,赵金熙.基于区域分解法的地下水有限元与边界元耦合模型:淄博市王旺庄水源地地下水数值模拟[J].地质论评,2003,49(1):48-52.(WANG Haoran,ZHAO Jinxi.A groundwater flow domain decomposition model coupling the boundary and finite element methods:A groundwater numerical simulation of the Wangwangzhuang water source area of Zibo City[J].Geological Review,2003,49(1):48-52.(in Chinese))

[29] O’MALLEY D,VESSELINOV V V.Analytical solutions for anomalous dispersion transport[J].Advances in Water Resources,2014,68:13-23.

[30] 魏恒,肖洪良.地下水溶质迁移模拟研究进展[J].冰川冻土.2013 (6):1582-1589.(WEI Heng,XIAO Hongliang.Advances in groundwater solute transport simulating reasearch[J].Journal of Glaciology and Geocryology,2013 (6):1582-1589.(in Chinese))

[31] 程金茹,郭择德.黄土包气带土壤水动力弥散系数的测定研究[J].辐射防护通讯,2001,21(5):24-26.(CHENG Jinru,GUO Zede.Determination of hydrodynamic diffusion coefficientfor soils in loess aerated zone[J].Radiation Protection Bulletin,2001,21(5):24-26.(in Chinese))

[32] PORRO I,NEWMAN M E,DUNNIVANT F M.Comparison of batch and column methods for determining strontium distribution coefficients for unsaturated transport in basalt[J].Environmental Science & Technology,2000,34(9):1679-1686.

[33] 宋树林,林泉.地下水弥散系数的测定[J].海岸工程,1998,17(3):61-65.(SONG Shulin,LIN Quan.Determination of the dispersive coefficientin groundwater[J].Coastal Engineering,1998,17(3):61-65.(in Chinese))

[34] QI Zhiming,FENG Shaoyuan,HELMERS M J.Modeling cadmium transport in neutral and alkaline soil columns at various depths[J].Pedosphere,2012,22(3):273-282.

[35] 刘勇,郑军芳,贾海红.西北某粘土矿水动力弥散系数的室内测定[J].环境科学与技术,2012(增刊2):319-321.(LIU Yong,ZHENG Junfang,JIA Honghai.In-lab determination of northwest clay mine hydrodynamic dispersion coefficient[J].Environmental Science & Technology,2012(Sup2):319-321.(in Chinese))

[36] 邵爱军,刘广明,杨劲松.土壤水动力弥散系数的室内测定[J].土壤学报,2002 (2):184-189.(SHAO Aijun,LIU Guangming,YANG Jinsong.In-lab determination of soil hydrodynamic dispersion coefficient[J].Acta Pedologica Sinica,2002 (2):184-189.(in Chinese))

[37] BRESLER E,NAOR A.Estimating transport parameters in soils by a maximum likelihood approach[J].Soil Science Society of America Journal,1987,51(4):870-875.

[38] JIN Y,PRATT E,YATES M V.Effect of mineral colloids on virus transport through saturated sand columns[J].Journal of Environmental Quality,2000,29(2):532-539.

[39] IIDA T,UEKI K,TSUKAHARA H,et al.Point physical model of movement of ions through natural snow cover[J].Journal of Hydrology,2000,235(3):170-182.

[40] 郭建青,钱会.分析一维砂柱弥散试验数据的反函数法[J].水利学报,1999(2):43-48.(GUO Jianqing,QIAN Hui.The inverse function method for analyzing the data of one-dimension sand column dispersive test[J].Journal of Hydraulic Engineering,1999(2):43-48.(in Chinese))

[41] 李合莲,陈家军.阻滞系数的确定方法及其应用[J].山东科技大学学报:自然科学版,2002,21(2):103-106.(LI Helian,CHEN Jiajun.Determination and application of retardation factor[J].Journal of Shandong University of Science and Technology:Natural Science,2002,21(2):103-106.(in Chinese))

[42] MEDINA I.Determination of diffusion coefficients for supercritical fluids[J].Journal of Chromatography:A,2012,1250:124-140.

[43] DO N Y,LEE S R.Temperature effect on migration of Zn and Cd through natural clay[J].Environmental Monitoring and Assessment,2006,118(1/3):267-291.

[44] MORADKHANI D,ESKANDARI S,SEDAGHAT B,et al.A study on heavy metals mobility from Zinc plant residues in Iran[J].Physicochemical Problems of Mineral Processing,2013,49(2):567-574.

[45] CHOTPANTARAT S,ONG S K,SUTTHIRAT C,et al.Effect of pH on transport of Pb2+,Mn2+,Zn2+and Ni2+through lateritic soil:column experiments and transport modeling[J].Journal of Environmental Sciences,2011,23(4):640-648.

[46] 廖敏.镉在土水系统中的迁移特征[J].土壤学报,1998,35(2):179-185.(LIAO Min.Transport characteristics of cadmiumin soil-water system[J].Acta Pedologica Sinica,1998,35(2):179-185.(in Chinese))

[47] BOND W J,SMILES D.Influence of velocity on hydrodynamic dispersion during unsteady soil water flow[J].Soil Science Society of America Journal,1983,47(3):438-441.

[48] PANG L,CLOSE M,SCHNEIDER D,et al.Effect of pore-water velocity on chemical nonequilibrium transport of Cd,Zn,and Pb in alluvial gravel columns[J].Journal of Contaminant Hydrology,2002,57(3):241-258.

[49] 章明奎,郑顺安,王丽平.土壤中颗粒状有机质对重金属的吸附作用[J].土壤通报,2008,38(6):1100-1104.(ZHANG Mingkui,ZHENG Shun’an,WANG Liping.Adsorption of heavy metals by soil particulate organic matter[J].Chinese Journal of Soil Science,2008,38(6):1100-1104.(in Chinese))

[50] 余贵芬,蒋新,孙磊,等.有机物质对土壤镉有效性的影响研究综述[J].生态学报,2002,22(5):770-776.(YU Guifen,JIANG Xin,SUN Lei,et al.A review for effect of organic substances on the availability of cadmium in soils[J].Acta Ecologica Sinica,2002,22(5):770-776.(in Chinese))

[51] BEKHIT H M,HASSAN A E.Two-dimensional modeling of contaminant transport in porous media in the presence of colloids[J].Advances in Water Resources,2005,28(12):1320-1335.

[52] DE JONGE L W,KJAERGAARD C,MOLDRUP P.Colloids and colloid-facilitated transport of contaminants in soils[J].Vadose Zone J,2004,3(2):321-325.

[53] CORAPCIOGLU M Y,JIANG S.Colloid-facilitated groundwater contaminant transport[J].Water Resources Research,1993,29(7):2215-2226.

[54] SAIERS J E,HORNBERGER G M.The role of colloidal kaolinite in the transport of cesium through laboratory sand columns[J].Water Resources Research,1996,32(1):33-41.

[55] FLURY M,QIU H.Modeling colloid-facilitated contaminant transport in the vadose zone [J].Vadose Zone J,2008,7(2):682-697.

[56] SAIERS J E,HORNBERGER G M.The influence of ionic strength on the facilitated transport of cesium by kaolinite colloids[J].Water Resources Research,1999,35(6):1713-1727.

[57] BAUMANN T,FRUHSTORFER P,KLEIN T,et al.Colloid and heavy metal transport at landfill sites in direct contact with groundwater[J].Water Research,2006,40(14):2776-2786.

[58] 尚熳廷,冯杰,刘佩贵.大孔隙对土壤水动力弥散系数影响的实验研究[J].灌溉排水学报,2009 (5):52-54,66.(SHANG Manting FENG Jie,LIU Peigui.Effect of macroporous on soil hydrodynamic dispersion coefficient[J].Journal of Irrigation and Drainage,2009(5):52-54,66.(in Chinese))

[60] 李国敏,陈崇希.空隙介质水动力弥散尺度效应的分形特征及弥散度[J].地球科学:中国地质大学学报,1995,20(4):405-409.(LI Guomin,CHEN Chongxi.Fractal geometry and estimation of scale-dependent dispersivity in geologic media[J].Earth Science:Journal of China University of Geosciences,1995,20(4):405-409.(in Chinese))

[61] 王永森,陈建生,陈亮.考虑弥散系数尺度效应的溶质运移模型研究[J].人民黄河,2008,30(11):60-62.(WANG Yongsen,CHEN Jiansheng,CHEN Liang.Research on solute transport model with scale-dependent dispersion coefficients[J].Yellow River,2008,30(11):60-62.(in Chinese))

Advances of dynamics model for heavy metal solute transport in aquifer

TAO An, LIU Shuguang, LOU Sha, DAI Chaomeng

(CollegeofCivilEngineering,TongjiUniversity,Shanghai200092,China)

On the basis of summarizing the study of the heavy metal pollution at home and abroad, the authors of this paper reviewed the development of dynamics model for heavy metal solute transport in aquifer, and summed up the calculation methods of the model.The authors also discussed the determination of model parameters and the influences of temperature, pH, pore-water velocity, organic matter and colloid, soil heterogeneity on the determination of parameters.At last, the authors pointed out the main problems existing in the study on the transport process of heavy metal solute in aquifer, and looked forward to the study that needs focusing on in the field.

groundwater; aquifer; heavy metal transport; numerical simulation; dynamics model; soil heterogeneity

10.3880/j.issn.1004-6933.2015.04.002

国家自然科学基金(41372240)

陶安(1990—),男,硕士研究生,研究方向为地下水数值模拟。E-mail:antao1990@163.com

刘曙光,教授。E-mail:liusgliu@tongji.edu.cn

P641.69

A

1004-6933(2015)04-0008-07