改进的混合遗传算法及其应用

刘克浩 肖飞龙

(湖北省疾病预防控制中心，湖北武汉 430079)



改进的混合遗传算法及其应用

刘克浩 肖飞龙

(湖北省疾病预防控制中心，湖北武汉 430079)

本文针对简单遗传算法的缺陷，设计了一种混合型搜索策略对算法进行改进。这种改进的算法归一化处理了复杂的约束条件，利用精英策略和轮盘赌策略选择最优个体，多点交叉和动态的变异操作使得种群保持多样性。通过改进，使得算法更小几率陷入局部最优，仿真实验表明，这种算法在稳定性、收敛精度上得到了较好的效果。

简单遗传算法；混合遗传算法；测试函数

遗传算法是一类起源于自然的智能启发式搜索算法。由 Holland[1]在 1975 年提出了这种智能优化算法，紧接着他的学生 Goldberg[2]在Genetic algorithms in search, optimization, and machine learning书中对简单遗传算法(SGA)做了完整的描述，这本书涉及到遗传算法的所有重要的参数讨论，包括交叉算子，变异算子，适应度计算等等，而且将遗传算法用到现实生活当中。遗传算法的主要特点是群体搜索策略和群体中个体之间的信息交换和搜索不依赖于梯度信息。作为启发式概率搜索的代表,遗传算法简洁明了，适应性强，而且可以易于并行化编程设计，在生物科学，数据挖掘，机械控制，智能优化等诸多领域有广泛的应用,成为本世纪关于智能计算非常重要的关键词。

区别于传统的优化方法，例如梯度下降法[3](gradient descent)、共轭梯度法[4](Conjugate Gradient)、牛顿法[5](Newton-Raphson method)等，这些数学优化算法理论往往需要对所求问题进行求导数或者偏导数，因此对于简单的问题也许能取得好的效果，但是对于那些维数高而又带有复杂苛刻约束条件的问题，不但需要目标函数具有良好的连续性，很容易陷入局部最优。在遗传算法当中，基因染色体的组成往往是首先进行编码，取代原有的数学表达方式，因此算法无论是离散、连续变量都能轻松解决。目标函数主导这个算法搜索过程的，不依靠其他辅助外界信息，这样没有必要需求设计函数或者解空间的平滑性和连续性，方便处理许多实际数学模型；另一方面，遗传演化算法在科学研究中有很多不同的研究方向，可以对算法的算法参数、搜索策略进行有效地改进，也可以与其他启发式算法进行融合，构成混合遗传算法。

1 混合遗传算法及其改进

启发式搜索算法的代表——遗传算法，为求解优化问题提供了一个模式，它不依赖具体问题，具有极强的鲁棒性。算法的基本单位为基因染色体，由众多染色体组成了种群。种群个体实际上是基因染色体编码组成，在整个可行域中不断进行进化搜索。种群中每个个体都被人为给予一个代表其搜索能力的值，称为适应度值(Fitness)，表示种群个体适应环境的能力，适应度越高，适应能力越强。

简单遗传算法(SGA)操作简单，适用于普通的优化问题，而针对多约束而且参数关系紧密的工程优化问题，其收敛速度和搜索精度会由于问题规模增加而下降，因此为了在一定程度上避免上述问题，提出相应的改进策略。

(1)遗传算法中的诸多参数会直接关联到最终的搜索效率和结果，通过实验效果修改相应的参数可以提高收敛效果。

(2)随迭代次数的递增, 演化得到的最优解在整个种群的百分比接近100%，意味着搜索结果在逐渐收敛，可以考虑将上一代的优良个体直接保存至下一代，加快收敛。

(3)在整个可行域的范围内不断迭代搜索的过程,根本上是由于在每次迭代过后增加了当前较好个体的存活概率，通过设计变异操作，刻意改变个体的搜索广度和搜索深度，以达到搜索整个解空间的效果。

在改进当中，值得注意的是，没有任何一种优化算法是能适应于所有的问题模型。Wolpert 和Macready在其论文当中提出了“No free lunch”理论[6]。

1.1 选择策略

当完成个体评价工作后，进入选择操作，这里采用混合策略，一方面保留部分种群中的精英个体，直接进入下一代的个体当中；另一方面利用罚函数的比例大小进行选择操作，在剩下的个体中选取产生余下的部分，两方面综合形成新的下一代个体。

Step1.对所有个体进行排序，选取前个个体作为精英(也就是说种群数目越大，精英个体的数目虽然增加，但所占比例减少，仍然保留了最优个体)

Step2.对剩余个体的罚函数值进行归一化处理，采用轮盘赌法选择个个体

1.2 交叉和变异策略

交叉操作的设置根据具体问题而定，如果问题的参数变量较多，通过约束条件看出变量之间的关联较多，建议采用多点交叉，交叉的段数范围在中随机取整生成,n代表变量的个数。关于变异操作，这里采取的策略是，能让种群在进化的早期尽可能的进行大规模搜索，在进化的晚期尽量在当前解集附近搜索，随着代数的增加，收敛速度由慢变快。根据以往的经验认为，如果变异概率大往往会丢失一些好的解，相反变异概率小会让种群早熟。

1.3 算法描述

Step1.确定算法的初始参数，初始化种群；

Step2.评估种群，计算适应度值函数和违约值，得到罚函数值；

Step3.对所有个体排序，先采用精英策略选择子代，剩余子代由轮盘赌生成；

Step4.遍历每个个体，确定每个个体的交叉位数，进行交叉操作；

Step5.遍历每个个体，对符合变异条件的个体进行变异操作；

Step6.检查算法是否结束，如是则结束输出结果；如否则返回step2，见图1。

图1 程序框图

2 仿真实验及分析

2.1 测试环境

硬件环境：Intel(R) Core(TM)2 Duo CPUT5750 2GHz RAM2GB

软件环境：Windows8 VS2012

2.2 测试函数

我们对混合遗传算法、普通遗传算法进行基本测试，使用一组标准的benchmark测试集函数。对不同算法，使用相同的种群规模和演化代数以及相同的算法参数(交叉率、变异率)，通过收敛速率、精度等相关系数进行比较。这组测试函数有的是单峰函数，有的是多峰函数，搜索空间的区分度比较大，包含不少局部最优点。

F1：Schaffer function

-10≤xi≤10

图2

F2:：Shubertfunction

图3

F3:Hansenfunction

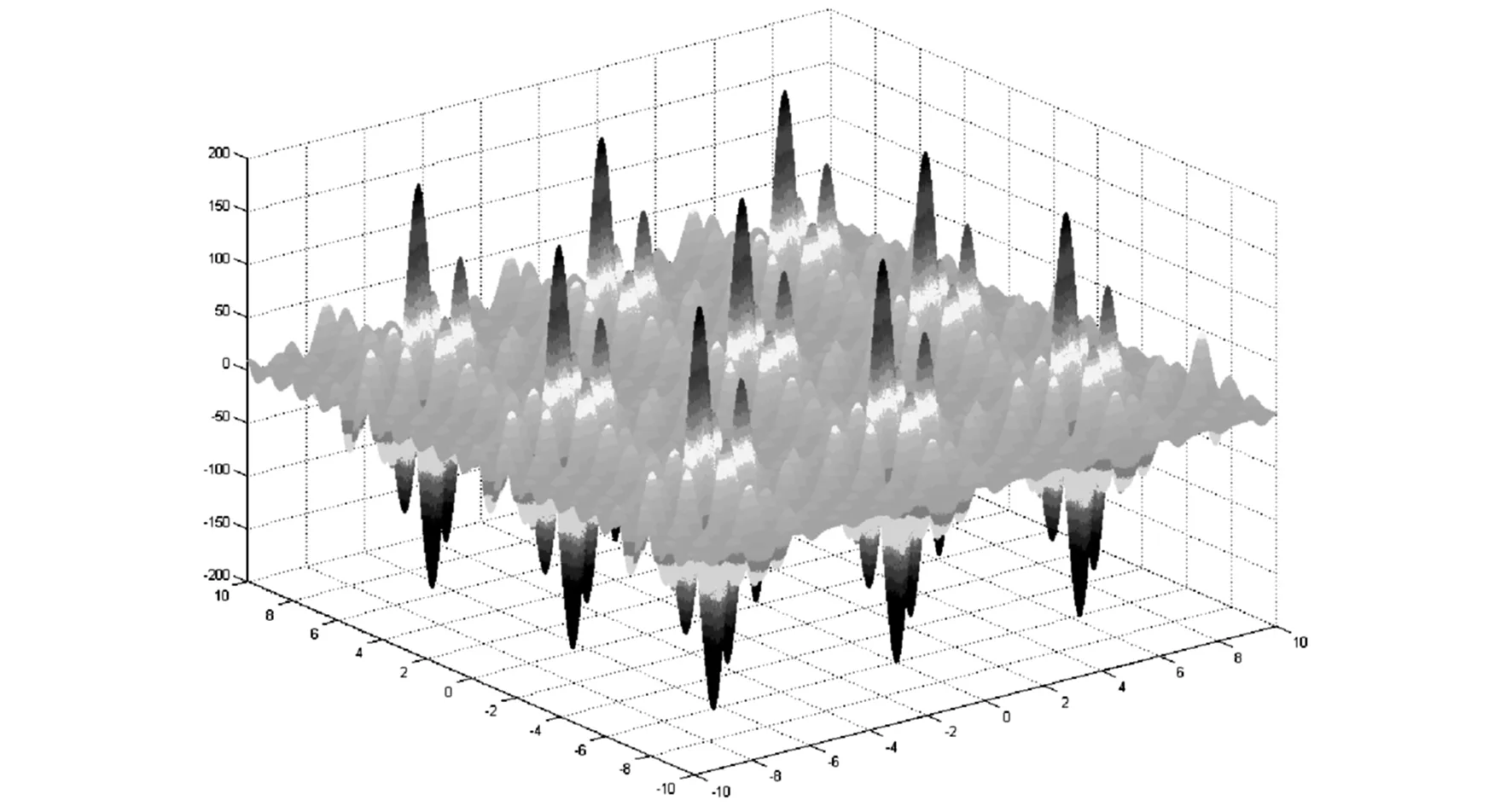
图4

F4:Camelfunction

+xy+(-1+4y2)y2x,y∈[-100,100]

图5

F5：

图6

F6：

minf(x,y)=-[xsin(9πy)+ycos(25πx)+20]x,y∈[-10,10]

图7

F7：

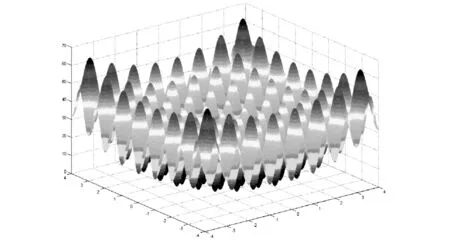
图8

F8：

图9

F9：

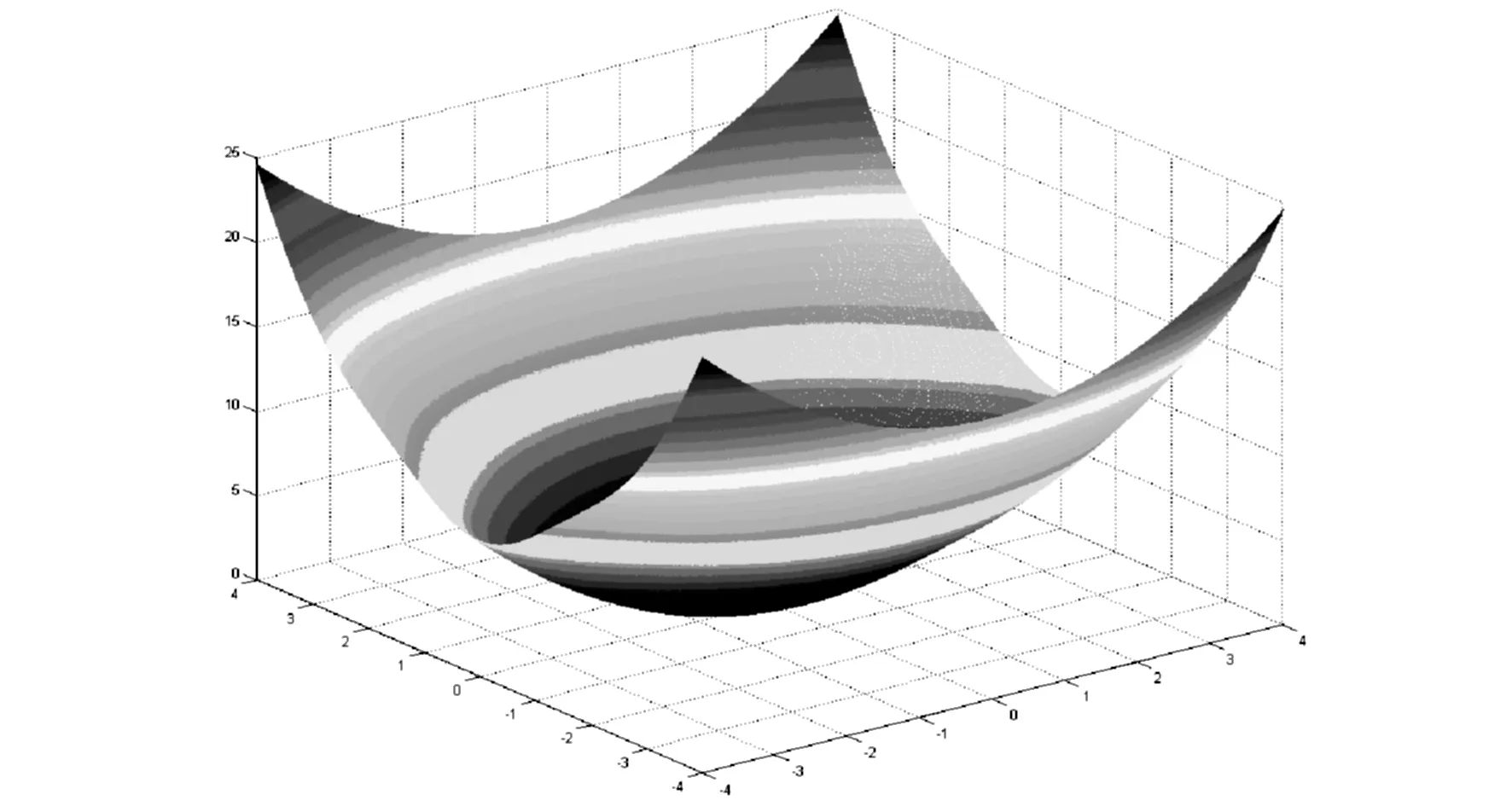
图10

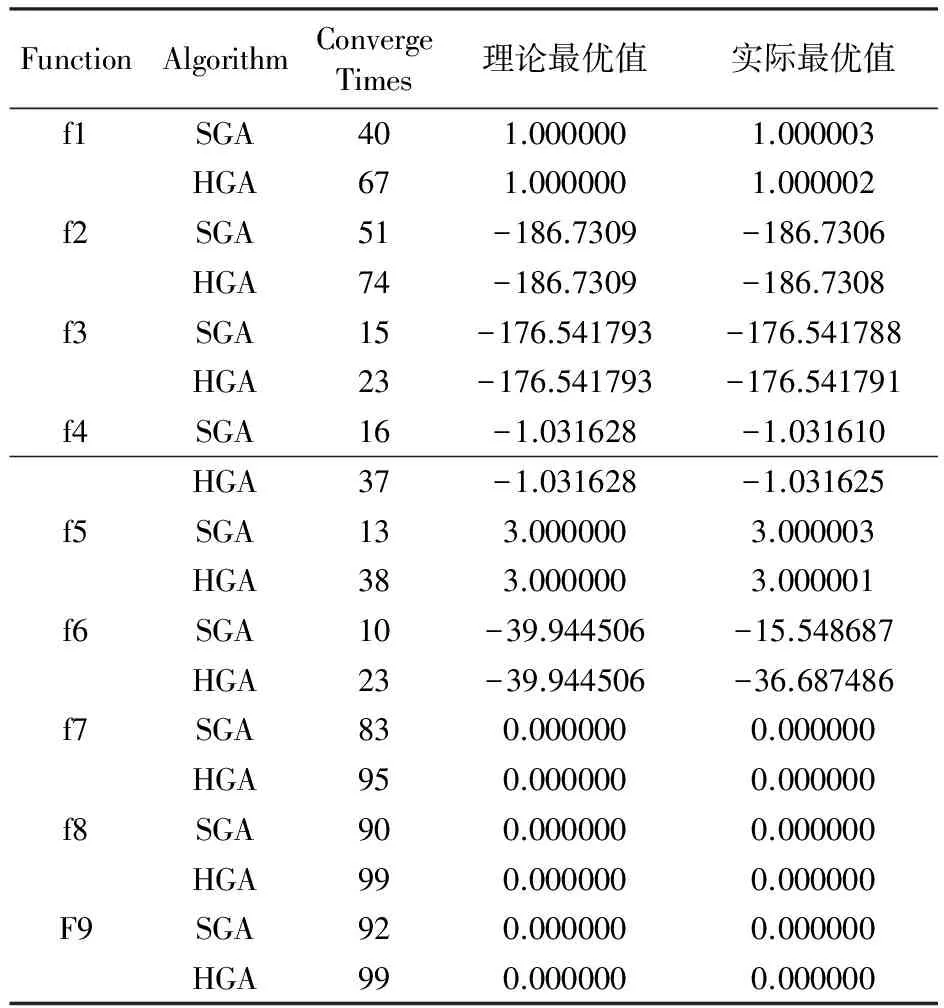
FunctionAlgorithmConvergeTimes理论最优值实际最优值f1SGA401．0000001．000003HGA671．0000001．000002f2SGA51-186．7309-186．7306HGA74-186．7309-186．7308f3SGA15-176．541793-176．541788HGA23-176．541793-176．541791f4SGA16-1．031628-1．031610HGA37-1．031628-1．031625f5SGA133．0000003．000003HGA383．0000003．000001f6SGA10-39．944506-15．548687HGA23-39．944506-36．687486f7SGA830．0000000．000000HGA950．0000000．000000f8SGA900．0000000．000000HGA990．0000000．000000F9SGA920．0000000．000000HGA990．0000000．000000

2.3 结果分析

对上述benchmark函数，两个算法均运行一百次，统计最终的结果。ConvergeTimes表示算法收敛到最优值的次数，次数越高，算法的稳定性越好。理论最优值表示该函数的最小值，实际最优值表示算法能达到的最优值，通过改进算法，混合遗传算法在收敛速度和收敛精度上都得到了一定的提高。对于F2，F3，F5，F6这种解空间中存在多个局部最优值的函数，改进遗传算法比SGA更加稳定，特别是F6，它的局部最优值非常多，SGA对处理这种欺骗性很大的函数非常困难，但混合遗传算法在跳出局部最优解这个问题上做的比SGA要好很多。

3 结 语

本文提出了一种混合遗传算法，这种算法归一化处理了复杂的约束条件，利用精英策略和轮盘赌策略选择最优个体，多点交叉和动态的变异操作使得种群保持多样性。通过一组benchmark函数的测试，表明混合遗传算法比普通遗传算法在收敛精度和稳定性等方面有很大的提高。

1HollandJH.Adaptationinnaturalandartificialsystems1sted.MITPress,1975

2GoldbergDE.Geneticalgorithmsinsearch,optimization,andmachinelearning[M].ReadingMenloPark:Addison-wesley, 1989

3MordecaiAvriel(2003).NonlinearProgramming:AnalysisandMethods.DoverPublishing

4MagnusR.HestenesandEduardStiefel(1952),Methodsofconjugategradientsforsolvinglinearsystems,J.ResearchNat.Bur.Standards49, 409-436.

5 Tjalling J. Ypma Historical Development of the Newton-Raphson Method SIAM Rev.37(4), 531-551

6 D. H. Wolpert and W. G. Macready, “No free lunch theorems for optimization”, IEEE Transactions on Evolutionary Computation, 1(1), 1997, pp.67-82

(责任编辑：谭银元)

The Improved Hybrid Genetic Algorithm and its Application Research

LIU Ke-hao,XIAO Fei-long

(Hubei Center for Disease Control and Prevention, Wuhan 430079, China)

In this paper, aiming at the defects of simple genetic algorithm, we design a hybrid search strategy to improve the algorithm. Normalization of this improved algorithm to deal with the complex constraints, using the elite strategy and roulette strategy choice the best individual, multipoint cross and dynamic mutation makes to keep population diversity. Through improvement, makes the algorithm more small chance to fall into local optimum, the simulation experiments show that this algorithm on the stability and convergence accuracy obtained better effect.

Genetic algorithm; Hybrid genetic algorithm; Benchmarks

2015-02-11

刘克浩，主要从事计算机应用方面的科研工作。

R394

A

1671-8100(2015)03-0034-04