PID预测控制算法在大迟延系统中的应用
2015-06-06马平赵倩
马平,赵倩
(华北电力大学自动化系,河北保定 071003)
PID预测控制算法在大迟延系统中的应用
马平,赵倩
(华北电力大学自动化系,河北保定 071003)
对于大迟延控制系统,传统的比例-积分-微分(PID)控制不能使其达到理想控制效果,而预测控制也存在结构复杂、参数多、在线计算量大、参数含义与实际系统的对应关系不明晰等缺点。综合PID控制与预测控制的优点,提出一种计算量小、易于工程实践且控制效果好的PID预测控制算法,将该算法应用于大迟延被控对象进行仿真研究。研究结果表明,PID预测控制算法能有效地解决大迟延系统的控制问题,提高系统的控制品质。
大迟延;PID控制;预测控制;鲁棒性
0 引言
在工业生产系统中,随着生产规模的不断扩大,机组容量也在不断增大,使得绝大部分被控对象具有不同程度的迟延[1]。在解决系统控制问题时,传统的比例-积分-微分(PID)控制方法以其原理简单、参数整定容易、鲁棒性强等优点一直被工程人员青睐[2],但对于大迟延系统来说,用传统PID控制方法得到的控制品质较差,不能满足工业需求。预测控制在理论上具有预测系统在一定控制作用下的行为、根据要求滚动求解最优控制作用、反馈修改预测模型的功能,能够有效解决大迟延系统的控制问题,并且在航空航天等领域取得了巨大成果[3],但预测控制的结构复杂、参数多、计算量大、参数含义与物理系统对应关系不明晰,在实际应用中工程人员很难接受。为了克服上述方法的不足,需要找到一种既具有预测模型、滚动优化、反馈矫正[4]的特征,同时又操作简单、易被工程人员熟练掌握的方法,即PID预测控制算法。
本文对PID预测控制算法和原始的PID控制算法进行系统响应试验、扰动试验、被控对象模型变化试验,试验结果表明:与普通PID控制算法相比,PID预测控制算法可有效克服大迟延系统在控制中存在的上述困难,具有更好的动态性能,增强了系统的鲁棒性。
1 PID预测控制算法分析
1.1 PID预测控制算法原理
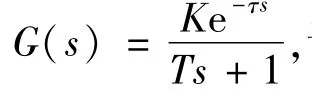
PID预测控制系统主要由预测器和控制器两部分组成,可以看作是对普通PID反馈控制的反馈环节增加了一个预测器。对于大迟延的被控对象,普通PID控制算法的控制效果必须经过迟延时间t之后才能够作用于被控对象并在系统的输出中得到体现,因此其控制作用对于大迟延对象总是具有t迟滞,控制效果较差;而PID预测控制的思想正是要通过预测器预测t之后的状态,把被控对象在当前控制作用下未来将达到的状态提前准确地反映给控制器,控制器根据预测器所预测的状态发出控制指令,使控制器的控制作用经过迟延时间t正好作用于被控对象上,以实现系统输出,更好地跟踪设定值。该结构采取的反馈矫正能够在一定程度上补偿模型失配、不确定性扰动等未知情况。应用PID预测控制算法去控制大迟延被控对象,等效于用PID算法去控制一个没有迟延的简单易控对象,故能有效解决系统的迟延问题,控制效果较好且容易在工程上应用。

图1 PID预测控制系统框图
综上所述,该算法从结构上看具有预测控制中预测模型反馈矫正两个特征,控制器采用PID控制,利用PID鲁棒性强的特点去替换预测控制的滚动优化求解最优控制作用,其结构简单、易于工程实践、控制效果好。
1.2 预测器的实现原理
在PID预测控制中,预测器通过模仿现场操作人员的思想与行为来实现对系统未来状态的预测,即根据被控对象现在和以前的系统输出值和变化率进行简单的在线计算,推导出系统在迟延t之后的状态(即被控对象未来t之后输出值与设定值的偏差),以利于控制器根据这些先验知识去调节大迟延被控对象,保证被控对象的输出能够很好地跟踪设定值。
图1中预测器的求取原理[5]为:把被控对象的输出看成在小区间内缓慢变化的曲线,用二次方程的形式表示系统的输出,随着时间的递进,二次方程的输出逼近变化的曲线。假设对系统t之后的状态做一个正确的估计,在求取系统的预测值之前,记k为系统的当前时刻,L为预测时间,k-L表示k时刻前L时刻,k+L表示k时刻后L时刻,当前时刻的输出为y(k),产生这一输出结果的控制器输出表示为μ(k)=Δμ(k)+μ(k-L),根据已知的输出y(k)和输出变化率˙y(k)对未来k+L时刻的输出和输出变化率进行预测,记预测值为(k+L)、预测值的变化为Δy(t),则被控对象输出的近似二次方程的形式如下
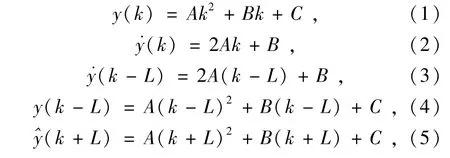
式中:A,B,C为常系数。
由式(2)和式(3)可以得到
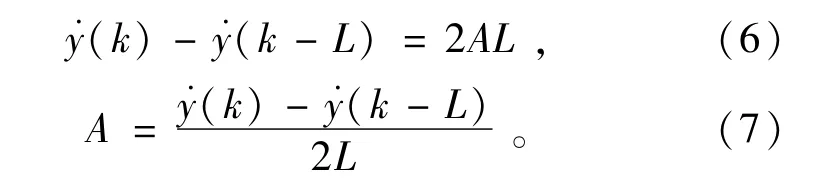
由式(1)和式(4)可以得到
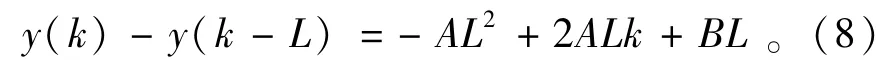
由式(1)和式(5)可以得到
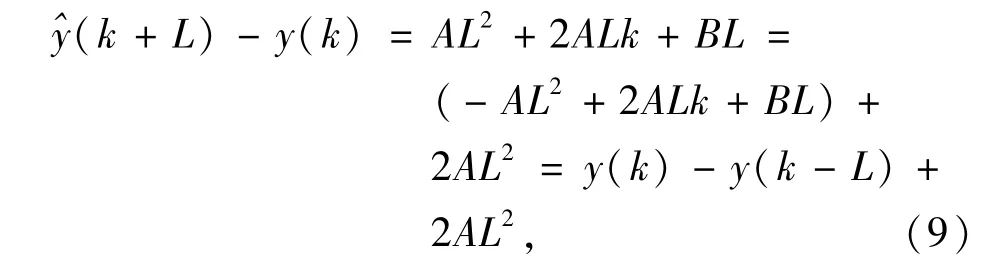
所以有
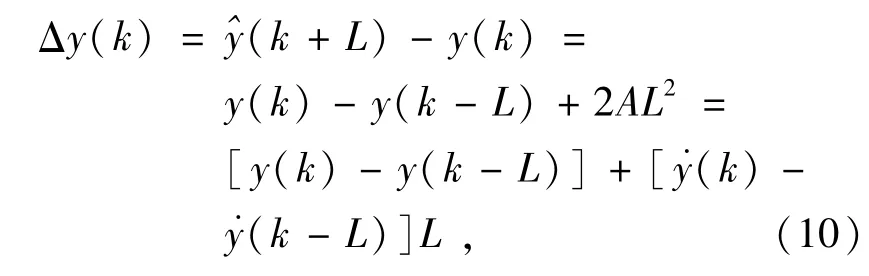
则预测输出值与设定值的偏差为


式中:R为设定值。
至此,根据k时刻以及k-L时刻系统的输出及输出变化率,利用数学算式推导得到k+L时刻系统输出值与设定值的偏差。
综上所述,PID预测控制在预测模型时不像传统预测控制采用阶跃响应、传递函数、状态方程等复杂的形式,而是把输出看成一条曲线,利用求导等简便方法计算系统未来的输出,大大减小了计算量,结构简单,易于工程实践。
1.3 PID预测控制算法参数设置
在式(11)中,系统进行控制时,预测器的目的是预测出系统迟延t之后的状态,所以预测时间L必须大于或等于t,对于这一状态既可以进行单步预测也可以进行多步预测[6]。记l为单次预测的预测步长,对不同的预测步长,系统的预测结果和实际状态差异不同,得到的控制效果也不同。
如果预测步长l等于预测时间L,则需进行单步预测,进行单步预测时要求控制增量可以保证输出一步达到设定值,但是此时控制增量的幅值很大,一般难以实施。所以,在实际应用中要在L时间内进行多步预测也就是多值预测。
对于多步预测的控制方法,要明确预测时间L及预测次数n。由于PID控制器的鲁棒性好,n的取值范围可以比较大,n的取值越大系统预测越准确,但同时计算量增大,预测所需时间也加长,所以一般定为4~8;另外,l为单次预测的预测步长,所以l的取值由n和L决定。
在式(11)的基础上可以推导出在l,2l,3l,…,nl时刻的系统输出与设定值之间的偏差e(t+l),e(t+2l),e(t+3l),…,e(t+nl)在某一点通过计算预测出未来的t+l,t+2l,t+3l,…,t+nl的n个点的值,并将其组成矩阵的某一行,当预测超过1次时预测值就可以组成一个误差矩阵
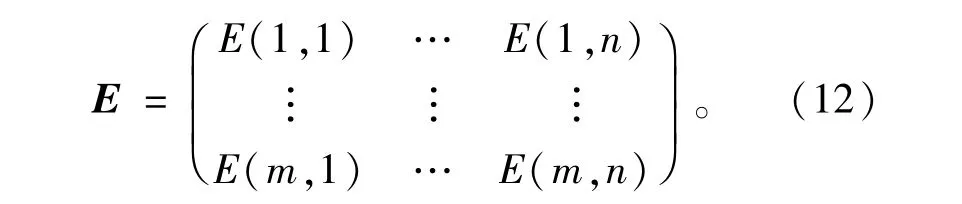
预测值的选取由误差矩阵E和预测次数决定。预测次数小于P(一般考虑计算量可以令P为3~5)次时预测值取最后一个值,当预测超过P次时预测值就取该点最后P次预测值的加权平均值。以此类推,滚动求解得到被控对象的预测模型。
综上所述,用滚动的方法去逼近被控对象预测模型,类似于预测控制中用滚动优化的方法求最优控制作用,这样求得的预测模型更加准确。工程人员根据最逼近的预测模型求解PID的控制参数,结合PID控制鲁棒性强的特点,控制效果能够达到最佳。
2 仿真分析
2.1 设定值扰动
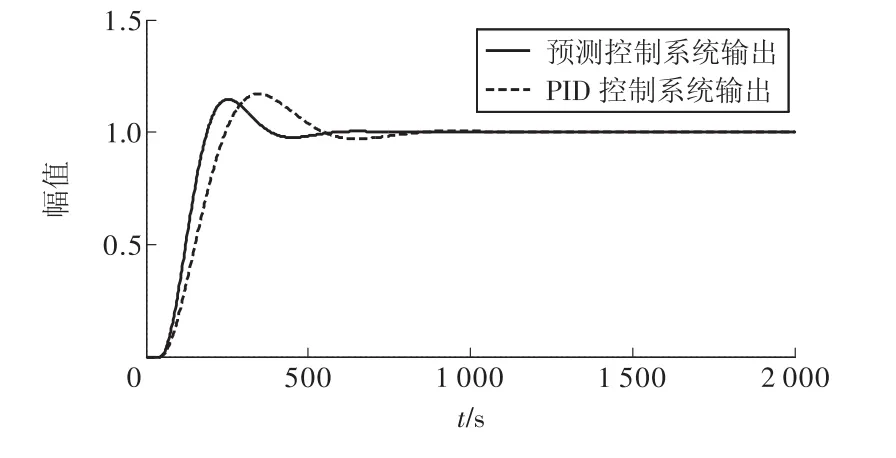
图2 PID预测控制系统输出与PID系统输出
试验结果表明:对于具有大迟延特点的被控对象,应用PID预测控制算法,系统在410 s达到稳定,其超调量为9.070 7%,应用普通PID控制,系统输出曲线在560 s达到稳定,其超调量为12.296 0%。综合以上可以看出,应用PID预测控制算法,被控对象的阶跃响应表现为调节时间短、超调小、能够明显改善系统的控制品质。
2.2 内部扰动
实际情况下,系统存在不同程度的内部扰动,对该大迟延系统加一个如图3所示的阶跃扰动。该扰动的幅值为0.5,进入系统的时间为第1 000 s,在两种控制方法的作用下,系统的输出曲线如图4所示。
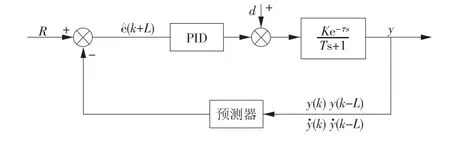
图3 系统加阶跃扰动
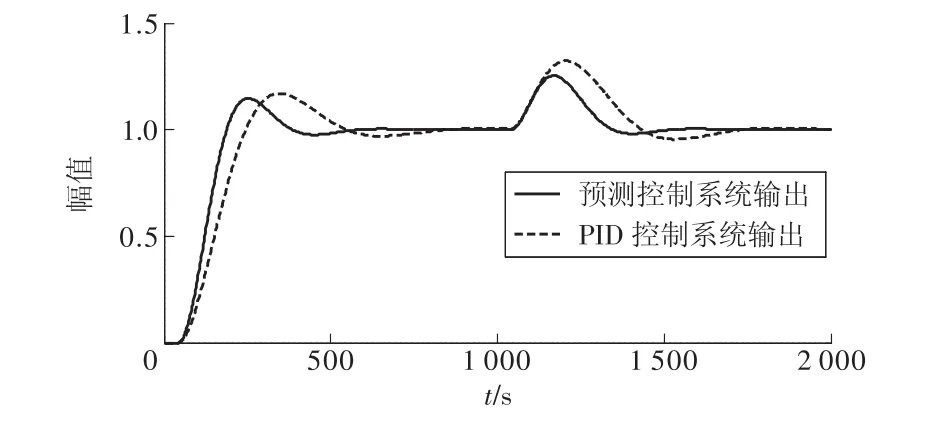
图4 加阶跃扰动后系统的输出曲线
由图4可以看出:在第1 000 s对系统加入幅值为0.5的阶跃扰动后,应用PID预测控制算法,系统在1322 s达到稳定,其超调量为25.3793%,应用普通PID控制,系统的输出曲线在1 656 s达到稳定,其超调为32.0718%。综合以上可以看出,应用PID预测控制算法,阶跃扰动的控制效果表现为调节时间短、超调量小、抗干扰能力强。
2.3 鲁棒性检验
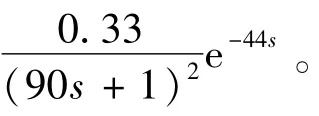
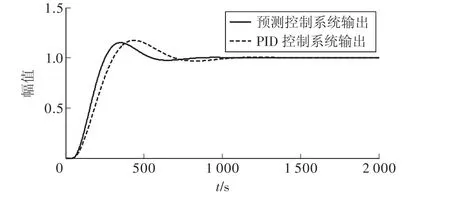
图5 被控对象模型参数变化后的系统输出曲线
试验分析:由图5可以看出,被控对象发生变化后,应用PID预测控制算法,系统在706 s达到稳定,超调为15.1376%,而应用普通PID控制时,系统在942 s达到稳定,超调为17.437 1%。综合以上可以看出,应用PID预测控制算法在被控对象发生变化时的控制效果表现为调节时间短、超调量小、鲁棒性强。
3 结论
本文在文献[5]提出的基于已知系统输出状态求系统未来状态预测模型的基础上,针对预测控制结构复杂、计算量大、参数多、参数与物理系统难以一一对应等特点,综合PID控制算法的参数设置容易、鲁棒性强的特点,提出了PID预测控制算法。应用此算法进行了阶跃响应、干扰、被控对象参数变化3个仿真试验,验证了PID预测控制算法相比普通PID算法的优越性。预测PID不仅能够有效克服被控对象的大迟延问题,提高了系统的快速性,而且抑制了系统的超调量,在系统存在扰动以及被控对象参数发生变化的情况下能够快速克服干扰,很大程度上提高了系统的控制品质。文中提出的PID预测控制算法结构简单、参数整定容易、在线计算量小,可以通过简单编程在物理实验室系统设备上实现控制,也可以经过简单的转换、组合,利用分散控制系统(DCS)用户自定义模块编程实现控制,是一种有推广价值的新型预测控制算法。
[1]王国玉,韩璞.预测控制及其在热工过程控制中的应用[J].电站系统工程,2002(3):53-56.
[2]杨丽华.预测控制及其在热工过程控制中的研究[D].北京:华北电力大学,2013.
[3]张春慧.预测控制算法及其在热工系统中的应用研究[D].北京:华北电力大学,2007.
[4]张嘉英,席东民,胡琳静.广义预测控制在锅炉燃烧控制系统中的应用[J].热力发电,2011(2):56-59.
[5]陈亮.循环流化床锅炉建模及其智能控制系统的研究[D].杭州:浙江大学,2005.
[6]王桂增,王诗宓,徐博文,等.高等过程控制[M].北京:清华大学出版社,2002:10-11,40-41.
[7]何同祥,杜瑶.一种改进的广义预测控制算法仿真研究[J].计算机仿真,2013(9):391-393.
[8]SAVITA G K,AMITK C,SONMATH N,etal.Modeling and monitoring of batch processes using principal component analysis assisted generalized regression neural networks(GRNN)[J].Biochemical Engineering Journal,2004,18(3):193-210.
[9]HAJISALEH M H,SALAHSHOOR K,SEFATM H.A new methodology for simulation and optimization of CO2sequestration in a saline aquifer using artificial neural network and model predictive control approach[J].Energy Sources,Part A:Recovery,Utilization and Environmental Effects,2014,36(3):336-346.
[10]席裕庚.预测控制[M].2版.北京:国防工业出版社,2013:274-277.
[11]韩璞,董泽,王东风,等.智能控制[M].北京:中国电力出版社,2013:144-150.
[12]金以慧.过程控制[M].北京:清华大学出版社,1993:312.
(本文责编:刘芳)
TP 273+.2
A
1674-1951(2015)07-0015-03
马平(1961—),女,湖南湘潭人,教授,硕士研究生导师,从事过程控制、火电厂单元机组控制和优化、计算机原理及应用等方面的教学科研工作(E-mail:maping2067@163.com)。
2015-03-17;
2015-06-23
赵倩(1988—),女,河北保定人,在读硕士研究生,从事预测控制在过程控制中的应用等方面的研究(E-mail:614243463@qq.com)。
