新型无刷直流电动伺服机构设计与分析*

陈 墨， 胡昌华， 张 伟， 方世鹏

(1. 第二炮兵工程大学302教研室，陕西 西安 710025；2. 第二炮兵工程大学403教研室，陕西 西安 710025)

新型无刷直流电动伺服机构设计与分析*

陈 墨1， 胡昌华1， 张 伟2， 方世鹏1

(1. 第二炮兵工程大学302教研室，陕西 西安 710025；2. 第二炮兵工程大学403教研室，陕西 西安 710025)

针对现役导弹伺服机构存在的结构复杂、加工精度高、体积重量大、价格昂贵、技术难度大、使用寿命短等缺点，结合某型号导弹伺服、电源配电系统工作实际，以无刷直流电机为驱动电机，设计了一种基于DSP的数字控制电动伺服系统，给出了设计方案和主要部件的工作原理，并对其进行了选型和性能分析，定量研究了伺服机构设计的可行性。最后进行了系统仿真，仿真结果表明系统具有良好的动、静态特性。

伺服机构； 无刷直流电机； 设计方案； 性能分析

0 引 言

伺服机构是导弹控制系统中的执行机构，接受控制系统给出的控制指令，控制发动机喷管的摆角，改变发动机的推力矢量，产生控制力矩，从而改变导弹的飞行姿态，使之按预定轨道稳定飞行。伺服机构是弹上除了发动机之外功率最大,工作温度、温升最高的设备[1]。现役导弹采用电动伺服执行机构，用液压油作为能源，虽然具有动态特性好、输出精度高、输出功率大等优点，其相比于电液伺服机构提供了更加理想的一种运动方式，配置简单单一的控制系统，并不需要诸如阀门、泵、过滤器、传感器等复杂的配套系统。同时，该机构具有体积质量小，工作寿命长，日常无需维护，不存在液压缸的液体渗漏污染情况，噪声显著减小、节能、干净、高刚性、超长寿命等优点，可长期工作并且实现高强度、高速度、高精度定位，运动平稳，能够较好地满足导弹对电动伺服机构提出的要求[2]。故研究并设计电动伺服机构对于导弹伺服机构的发展具有重要意义。无刷直流电机具有结构简单、寿命长、效率高和较好的转速-转矩特性等优点[2]。故本文选取无刷直流电机作为驱动电机，结合某型号导弹的电源配电系统工作实际以及伺服机构的使用工况，设计电动伺服机构并对其主要部件的性能及误差进行了分析，定量地验证了系统设计的可行性。

1 电动伺服系统的组成及原理

该电动伺服系统由伺服电机、伺服电机驱动器、制动电阻、减速器、位置反馈装置(编码器)、极限位置限位装置、伺服装置本体、气压平衡装置及传动装置组成。其中电动伺服机构体及传动装置主要包括减速器、齿轮副、滚子丝杠副、轴承组、推杆、缸筒等。电动伺服机构是将伺服电机与丝杠一体化设计的模块化产品，通过减速传动装置将伺服电机的旋转运动转换成直线运动，同时将伺服电机精确转速控制、精确转角控制、精确扭矩控制转变成机构的精确速度控制、精确位置控制、精确推力控制，从而实现高精度直线运动。其主要传动原理就是将电机的旋转运动通过滚子丝杠副的机械运动转换为推杆的直线运动，并利用伺服电机的闭环控制实现对推杆的推力、速度和位置精密的控制。

这种设计优点很多，在电动伺服机构运动全过程中能够通过失电制动器实现锁定功能；可实时反馈伸出行程，运行中间位置停止，重新起动后反馈当前的绝对位置；当指令行程超出极限位置时，能够提供可供I/O端口接收的故障反馈信号，以及过压保护、极限限位、报警等功能，大大提高了系统的可靠性和稳定性，节约了使用成本。

2 系统方案总体设计

该电动伺服系统主要由DSP主控电路、功率驱动电路、主电路、信号检测电路组成，如图1所示。

图1 系统设计总体框图

位置信号由上位机给出，速度信号由位置信号经计算得出，主控芯片选用TI公司生产的TMS320F2812，其是一款新型32位定点DSP芯片，片内带Flash存储器，工作频率达到150MHz，还集成了多种外设，非常适用于电机控制领域[3- 4]。

系统设计采用全数字三闭环控制，控制框图如图2所示，上位机通过1553B[5]通信给出位置信号，位置传感器(光电式多圈绝对值编码器)通过测量丝杠旋转圈数，反馈电动伺服机构推杆行程，得到伺服机构的实际位置，经过微分计算得到速度信号，通过速度环与电流环产生一定脉宽占空比的PWM波驱动控制电机，然后通过减速器与行星丝杠副的作用使推杆作直线运动驱动负载。之后当接收到姿态控制系统给出的位置、速度指令，在控制系统的作用下，采用一定的DSP算法，使机构稳定在指定位置。

图2 伺服系统控制原理框图

3 主要部件的性能分析

3.1 滚珠丝杠副的选型计算

导弹伺服机构需要提供大的推力，根据实际工作工况，针对额定推力不小于Fa=12000N的要求对电动伺服机构使用的滚子丝杠副进行选型计算。

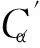
根据丝杠副的参数分别计算以下数据。

螺母的预紧力：F0=0.06Cα

(1)

轴向动载荷：Fa动=Fa+Fo

(2)

丝杠副理论要求总转数为

(3)

丝杠副实际额定寿命(总转数)为

(4)

式中：Fa总——总轴向载荷，大小为Fa动;

fw——负荷系数，查选型册取值为1.5。

根据计算结果可知丝杠副额定寿命可以满足实际使用要求，寿命安全系数为1.17。

丝杠副的基本额定静载荷计算值为

(5)

式中：Fa静——轴向静载荷；

fs——静安全系数，取值为2.5。

根据计算结果可知丝杠副额定静载荷可以满足实际使用要求，静载荷安全系数为1.4。

(2) 丝杠副所需转矩计算。依照导弹伺服实际工况，电动缸需产生不小于12000N的推力，满载最大稳定速度不小于180mm/s，最大稳定速度按照180mm/s计算，结合丝杠副导程，得丝杠副转速n丝杠为

n丝杠=60v/Ph

(6)

丝杠副的效率：

η丝杠=η滚动·η滚子轴承

(7)

式中：η滚动——滚动丝杠效率，范围为0.85～0.95，取η滚动=0.9；

η滚子轴承——滚子轴承效率，取η滚子轴承=0.98。

丝杠副的额定输出动转矩T丝杠输出为

T丝杠输出=5Fa/2000π

(8)

丝杠副的额定输入动转矩T丝杠(动)为

T丝杠(动)=T丝杠输出/η丝杠

(9)

丝杠副所需输入功率P丝杠为

P丝杠输入=T丝杠(动)·n丝杠/9550

(10)

(3) 丝杠副临界压缩载荷Fc的校验(验算压杆稳定性)。

(11)

式中：d1——丝杠副螺纹底径，23.5mm；

la——丝杠副安装间距80mm；

η2——与安装方法相关的系数，所采用的安装方法为固定-支撑，η2=10。

代入数值得

Fc>F0

(12)

根据计算结果可知丝杠副临界压缩载荷可以满足使用要求。

(4) 丝杠副极限转速nc的校验。

(13)

式中：λ2——与安装方法相关的系数，所采用的安装方法为固定-支撑，λ2=15.1。

则：

nc>n丝杠

(14)

根据计算结果可知丝杠副极限转速可以满足使用要求。

综上计算，选取日本THK公司生产的BNFN2505丝杠副可以满足使用要求。

3.2 伺服电机的选型计算

(1) 伺服电机的转速计算。伺服电机的转速选择为n电机=6500r/min，传动系统的总传动比为

i=n电机/n丝杠

(15)

设计齿轮传动的速比为二级传动，减速比分别为i1=1.6，i2=1.9。

根据伺服电机转速n电机，复算电动缸满载最大稳定速度：

(16)

接近满载最大稳定速度不小于180mm/s的技术要求及设计要求。

(2) 伺服电机的转矩计算。整个减速传动环节的效率η减速：

η减速=η1·η2

(17)

式中：η1——一级传动效率，η1=0.98；

η2——二级传动效率，η2=0.98。

电机输出转矩T电机输出为

(18)

伺服电机的额定扭矩4N·m，满足设计及使用要求。伺服电机的安全裕度w电机=1.03，同时，对应的电动伺服机构设计推力F推为

F推=Fa·w电机

(19)

(3) 伺服电机制动力矩计算。根据技术要求，锁紧力在失电状态下、全行程范围内，承受最大轴向载荷不小于12000N。

螺母的预紧力为F0=0.06Ca，轴向静载荷为

Fa动=Fa-Fo

(20)

伺服电机输出轴静载转矩T电机(静)：

(21)

伺服电机制动器额定制动扭矩为3.6N·m，满足设计及使用要求。制动器的安全系数w制动=1.37，其中锁紧力为

T紧锁力=Fa·w制动

(22)

4 系统定位精度计算

4.1 机械传动系统误差

(1) 齿轮传动环节装配误差。传动系统的第一级传动装置，根据传递的扭矩计算其间隙f间1=3′，折算到第二级传动误差值ε1为

ε1=f间1/i2

(23)

传动系统的第二级传动装置，根据传递的扭矩计算其间隙为f间2=3′，折算到丝杠副传动误差值ε2为

ε2=f间2+ε1

(24)

回程间隙折算到电动缸行程上的误差ε行程1为

(25)

(2) 齿轮副侧隙误差计算。减速换向环节传动装置，其内部为两级齿轮传动。两组齿轮副都设计为6级精度斜齿轮。

第一级齿轮副最大侧隙计算如下。

齿轮副安装制造误差Jn为

(26)

式中：fpb——基节极限偏差，fpb1=fpb2=fptcosαn=0.011mm；

fpt——单个齿轮极限偏差，结合小齿轮和堕轮的分度圆直径及模数，取fpt1=fpt2=0.012mm；

αn——压力角，取αn=20°；

Fβ——螺旋线总偏差，结合堕轮的分度圆直径，取Fβ=0.017mm。

齿轮副总误差计算：

(27)

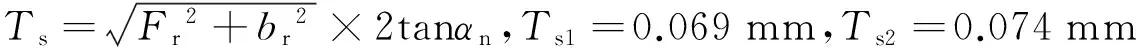
Fr——径向跳动公差，结合小齿轮和堕轮的分度圆直径及模数，得Fr1=0.036mm,Fr2=0.05mm；

br——基节制造偏差，br=0.088mm；

fα——中心距公差，结合小齿轮和堕轮的中心距，查机械设计手册fα=0.027mm。

由上述计算可知，第一级齿轮副最大侧隙为0.094mm，折算在行程上的误差为0.012mm。计算过程如下：

根据堕轮分度圆直径d堕轮=36.265mm和丝杠副导程Ph计算行程上的误差为

ε行程2=TjnSh/d堕轮

(28)

第二级齿轮副最大侧隙计算如下。

齿轮副安装制造误差计算：

由式(26)得Jn=0.025mm。

fpb=fptcosαn

(29)

(30)

结合堕轮和大齿轮的分度圆直径及模数，取：fpt1=0.012mm,fpt2=0.013mm。

结合大齿轮的分度圆直径，取Fβ=0.018mm。

齿轮副总误差计算：

由式(27)得Tjn=0.099mm。

Ts1=0.069mm，Ts2=0.074mm

Fr1=0.036mm，Fr2=0.05mm

由上述计算可知，第二级齿轮副最大侧隙为0.099mm，折算在行程上的误差为0.0076mm，计算过程如下：

根据大齿轮分度圆直径d齿轮=65.075mm和丝杠副导程Sh计算行程上的误差为

ε行程3=TjnSh/d齿轮

(31)

所以因齿轮传动误差引起的导程误差为

(32)

(3) 丝杠副导程误差。根据《THK综合产品目录A册产品技术说明》的选型说明，选择滚子丝杠副的导程精度等级为C6。按照此项精度等级规定运行距离误差经计算，电动伺服机构在有效行程75mm内的导程误差为0.13mm。 由于丝杠具有预压力，所以其没有反向间隙。

机械传动设计最大误差为0.159mm。

4.2 电控系统误差

(1) 电子齿轮设定误差。根据本次方案设计中丝杠导程5mm，减速比为3.01，按照1个脉冲当量对应电动缸行程为0.001mm计算，电子齿轮比为4096/1000，设置驱动器电子齿轮分子为4096，分母为1000，与要求值相同，即电子齿轮设定没有引入误差。

(2) 伺服驱动器到位允许误差。伺服驱动器到位允许误差设计值为50，按照电子齿轮比的设定，1个脉冲当量对应电动缸行程为0.001mm，即产生的误差为0.05mm。

电控系统最大误差为0.05mm。

(3) 反馈装置误差。本次设计选取某公司生产的EQN425多圈绝对值编码器，其精度为±1LSB，对应反馈精度为±0.00195mm。

综上所述，电动伺服机构定位精度最大误差为0.21mm。

5 系统仿真

结合主要部件的性能参数，以无刷直流电动伺服机构为被控对象，考虑负载为一阶惯性环节，控制部分采用三闭环控制，电流环采用积分分离的PI控制算法，速度环采用改进型的PI控制算法，位置环采用CMAC与PID复合控制算法[7-8]，在MATLAB环境下进行仿真[9]。

从仿真曲线可以看出： 初始时，给定行程为0mm，系统响应平稳，静态误差小；在t=1s前系统达到稳定状态，待系统接收到推杆行程指令，在该行程的电机转速下系统达到稳定的时间只有25ms，无超调，稳态误差小于1mm；t=1.25s时系统加入负载，转速突然降低，但又迅速恢复到给定值，鲁棒性强，系统经30ms后重新稳定，系统控制的实时性快速响应性较好，能够较好地满足系统的控制指标要求。系统的仿真曲线如图3所示。

图3 系统仿真曲线

6 结 语

本文分析了现役导弹伺服机构存在的不足，提出了一种新的电动伺服机构设计，给出了系统整体设计方案，分析了其组成、原理，对主要部件进行了性能分析，定量地描述了机构设计的可行性，最后在MATLAB环境下进行了试验仿真，仿真结果表明该系统具有较强的鲁棒性和实时性，这对后续电动伺服机构工程在导弹上的整体实现与应用具有很大的理论指导意义和参考价值。

[1] 胡昌华，马清亮，郑建飞.导弹测试与发射控制技术[M].北京： 国防工业出版社，2010.

[2] PILLAY P, KRISHNAN R. Application characteris-tics of permanent magnet synchronous and brushless DC motors for servo drives[J]. IEEE Transactions on Industry Application, 1991,27(5)： 986-996.

[3] 王国伟，赵吉文.基于DSP2812的无刷直流电机控制系统研究[D].合肥： 安徽大学，2010.

[4] LUO Y, LI H, SHEN M Y. Speed control of BLDCM for industrialsewing machine based on dSPACE[C]∥2006 IEEE International Conference on Mechatronics and Automation, ICMA 2006,2006: 2127-2132.

[5] DDC. ACE/Mini-ACE series BC/RT/MT advanced communication engine integrated 1553 terminal user’s guide[G]. New York： Data Device Corp, 1999.

[6] 宋轶群，杜华生，王德新.基于CMAC神经网络与PID的并行控制器设计与应用[J].控制系统，2005(3)： 37-39.

[7] 胡金竹，谢寿生，翟旭升.基于CMAC和PID算法的发动机导流叶片控制系统[J].弹箭与制导学报，2009，29(4)： 154-156.

[8] 叶振锋，雷淮刚.基于MATLAB的无刷直流电动机控制系统仿真[J].驱动控制，2006(3)： 19-21.

[9] 刘海珊，陈宇晨.无刷直流电机PID控制系统仿真及实验研究[J].系统仿真学报，2009，21(16)： 5157-5160.

Design and Analysis of A New BLDCM Servomechanism

CHENMo1，HUChanghua1，ZHANGWei2，FANGShipeng1

(1. Faculty 302, The Second Artillery Engineering University, Xi’an 710025, China;2. Faculty 403, The Second Artillery Engineering University, Xi’an 710025, China)

By analyzing the shortages of the current missile servomechanism which has complex structure, high machining accuracy, large volume weight, difficult technology, short lifetime, a new digital servo control system using brushless dc motor as a servo motor, combined with the model number actual missile servo, power distribution systems based on DSP was presented. The system scheme was designed and the performance parameters of its main components were analyzed. Then simulate the control system and the simulation results showed that the system had a good dynamic and static characteristics, and verified the feasibility of the system design.

servomechanism; brushless DC motor; design scheme; performance analysis

国家自然科学基金杰出青年项目(61025014)；国家自然科学基金面上项目(61021063,61028010,60736026)

陈 墨

TM 921.54+1

A

1673-6540(2015)05-0006-05

2014-08-25