需求信息不对称下双渠道供应链的协调
2015-06-05张来江颜荣芳
张来江, 颜荣芳
(西北师范大学 数学与统计学院 ,甘肃 兰州 730070)
需求信息不对称下双渠道供应链的协调
张来江, 颜荣芳
(西北师范大学 数学与统计学院 ,甘肃 兰州 730070)
基于报童模型,研究了由一个制造商与一个零售商组成的双渠道供应链在需求信息不对称条件下的契约协调问题,分别得到了离散和连续两种需求类型下的最优回购契约,并分析了最优回购契约对供应链的协调绩效.
双渠道供应链;信息不对称;回购契约;供应链协调
1 引 言
随着信息技术和物流技术的飞速发展,越来越多的企业在通过传统零售渠道分销商品的同时,开通了网络直销渠道,业已形成了传统渠道和网络直销并存的双渠道销售体系,双渠道销售已经成为当今制造业零售的主流模式.
然而,电子直销渠道的引入使传统零售商对制造商不再信任,不再完全传递或共享真实的信息给其制造商,出现了信息不对称的现象,所谓信息不对称,是指某个或某些供应链节点企业拥有的,其他成员无法了解的私有信息,在供应链管理中信息不对称现象普遍存在,如制造商拥有更多关于生产能力,产品质量和生产成本等方面的信息,而零售商拥有更多关于销售成本, 市场预测等方面的信息,企业单边信息不对称将会导致逆向选择问题,使决策者的决策变量(如产量,订货量等)产生扭曲,从而破坏供应链协调,影响供应链的效率.在更多的供应链实践中,拥有私人信息的企业往往以自己的收益最大化为目标而不是考虑整个供应链的收益,隐匿或者谎报信息的行为有可能发生,这使得供应链更容易导致双重边际化效应和牛鞭效应等低效率行为,因此在信息不对称下供应链的协调机制研究越来越受到关注,供应链协调的实现就是使分散决策中的个体的行为和集中决策中的个体行为保持一致,有效的契约协调机制是提高供应链效率的重要手段,以下文献在不同的信息非对称条件之下对供应链的定价与协调机制进行了研究.如Metin等(2010)[1]分析了一个供应商和一个零售商组成的单渠道供应链,在制造商的单位生产成本信息非对称下,零售商给其供应商提供契约组合的逆向选择博弈,并探讨了最优契约组合可以协调渠道的依赖条件;Liu和Ozalp(2010)[2]研究了制造商拥有新产品需求更新信息的单渠道供应链,分析比较了价格数量弹性契约对供应链绩效的影响;ErbaoCao等(2013)[3]研究了成本信息不对称下双渠道供应链的协调问题,给出了在批发价契约下的平衡定价与利润,并分析了零售商的成本信息对各参与方及系统利润的影响;VolodymyrBabich等(2012)[4]在随机需求下,研究了由一个制造商与一个零售商组成的单渠道供应链在需求信息不对称条件下的契约协调问题,分别得到了离散和连续两种需求类型下的最优回购契约;Mukhopadhyay等(2008)[5]研究了需求信息非对称下制造商为领导者的双渠道供应链定价策略,并讨论了需求受价格和服务影响时,服务成本信息不对称下的最优决策;Yue和Liu(2006)[6]研究了信息共享对定价的影响,同时也分析了供应链主体对信息共享的态度;Yan和Pei等(2011)[7]研究了信息不对称下双渠道供应链中信息共享对制造商和零售商利润的影响,研究发现信息共享下制造商的利润总是增加的,但对零售商利润的影响并不明显;Yao等(2005)[8]分别探讨了信息对称和不对称给回购契约下制造商和零售商收益的影响;Hsieh等(2008)[9]以单个供应商和单个零售商组成的供应链系统为研究对象,在需求信息不对称的情况下,研究了单产品短生命周期的联合决策问题;Gong(2008)[10]研究了供应商与零售商在信息不对称的情况下,最优的回购契约并不总能实现。Gan等(2010)[11]研究了需求信息不对称下供应商代发货供应链中,供应商可提供一个承诺处罚契约组合来获取零售商的需求信息,并得到了使供应商期望利润最大化的最优解;Xiao和Yang(2009)[12]探讨了一个制造商和一个零售商在需求不确定下面对外部整合竞争者时, 制造商采用改进的批发价格契约使零售商如实报告其风险敏感性信息,以提高供应链绩效;Xu等(2010)[13]给拥有私人成本信息的制造商备用供货商,建立了一个含有转移支付和提前期的最优批发价格契约模型.需要说明的是,以上所提到的绝大多数研究者都是基于随机需求的单渠道,成本信息不对称以及简单的回购契约等来展开的.在随机需求下,考虑零售商掌握市场需求类型这一私有信息即零售商的需求信息不对称,利用拥有转移支付的回购契约,在离散和连续的需求类型状态之下,从最优订购量和在线生产量的角度研究了制造商双渠道供应链的协调策略.
2 两种需求状态的模型
考虑由一个制造商和一个零售商组成的双渠道供应链,其中制造商为Stackelberg领导者,而零售商为跟随者。假设市场中仅有一种产品,制造商可以通过传统渠道和直销渠道同时向消费者销售这一产品。记制造商和零售商的成本分别为cm和cr,直销价和零售价分别为pm和pr,制造商以批发价w将产品分销给零售商,制造商在线渠道的生产量为Qm,零售商给制造商承诺的订购量为Qr,零售商未售出的产品制造商将以价格b回收,此外零售商需支付制造商固定费用T.
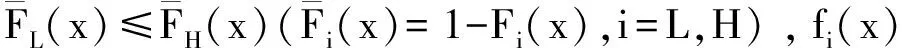

该契约由回购价b,单位批发价w,固定的转移支付T组成,可表示为(wi,bi,Ti), 其中(wL,bL,TL)是为低类型零售商设计的契约,而(wH,bH,TH)是为高类型零售商设计的契约.在满足零售商的个人理性约束(IR)与激励相容约束(IC)之下,使制造商的期望利润最大化,可求得契约组合中相对应的值.设定(IR)约束是为了让零售商的利润在真实表露市场需求的情况下大于其保留利润π0,保证了零售商参与双渠道供应链的积极性.(IC)激励相容约束是用来引诱零售商选择能窥测其类型即市场需求类型的约束.
零售商观察市场类型选择其中一组契约,并告知制造商其承诺的订购量Qri(i=L,H),制造商则会根据零售商的选择所透露出的市场需求类型,来安排其线上和线下渠道的生产量,待真实的市场出现之后,再将零售商未售出的产品以协定的单位价格b回收.
出于讨论方便,假设缺货成本和挽救价值对于制造商与零售商来说均为零,对一些参数关系加以说明:
1)w∈[0,n],b∈[0,m],即w和b是有界的.
2)bi 容易得到零售商的利润Πr和制造商的利润Πm分别为 Πr=(pr-cr)min(Qr,Dr)-wQr +b(Qr-Dr)+-T, 和 Πm=pmmin(Qm,Dm)-cmQm+(w-cm)Qr -b(Qr-Dr)++T, 其中Qr为零售商的订购量,Qm为制造商在线渠道的生产量,(Qr-Dr)+为零售商未售出的产品数量.注意到min(D,Q)=D-(D-Q)+,(X-Q)+=max(X-Q,0),因此 Πr=(b-pr+cr)(Dr-Qr)+ +(pr-cr-b)Dr+(b-w)Qr-T, Πm=pmDm-pm(Dm-Qm)+-cmQm +(w-cm)Qr-b(Qr-Dr)-b(Dr -Qr)++T. 当i型零售商选择j型契约时,其期望利润 -(wj-bj)Qr-Tj(i,j=L,H). (1) 记零售商承诺的最优订购量 (2) 将式(2)代入式(1), 得 (3) 类似地,可以将i型零售商选择j型契约时制造商的期望利润表示为: (4) 于是,由式(3)和(4)可得集中式情形下系统的期望总利润 由于集中式情形下信息对称,因此制造商只需决定产品的产量。容易证明E[Πc]关于Qmi,Qri是联合凹的。由期望总利润最大化的一阶条件立即得到制造商在线渠道的最优生产量和零售商的最优订购量分别满足 因此, 制造商的决策问题可以表示为如下的最优化问题: (A1) 从零售商承诺的最优订购量满足的条件(2)可得 (5) QrHL>QrLL, (6) 因此,当(IR-1)和(IC-2)满足时(IR-2)自然满足,从而约束(IR-2)可被去掉.注意到 当约束(IR-1)和(IC-2)的等号成立时, (7) (8) 将式(7)和(8)代入式(A1)可得 由一阶条件可得 再结合式(5), 得到最优解满足的条件 (9) (10) 因此(IC-1)在约束(IR-1)和(IC-2)满足的最优解下自然成立, 从而这一约束可以被去掉。 于是得到下面的命题. 命题1 由制造商最优决策问题所确定的对两类零售商的最优契约为 ii)最优批发价 iii)最优转移费用 -π0, (11) (12) 注2 在最优解中Q*rHH=QcrH,Q*rLL≠QcrL,Q*mHH=QcmH,Q*mLL=QcmL,说明对于制造商来说的最优解,并不是整个供应链中的第一最优解,即只有在高类型市场需求下,在线生产量与零售商订购量才能达到集中式最优,使渠道得到协调,而在低类型市场需求下零售商未达到集中式最优,制造商却达到了集中式最优. 制造商的决策问题可以表示为如下的最优化问题: (A2) 其中,E[Πr(φ,ψ)]表示φ型零售商选择ψ型契约时的期望利润,E[Πm(φ)]表示面对φ型零售商时制造商的期望利润.设定(IR)约束要求任何需求类型的零售商在真实的表露市场类型时,其期望利润必须大于保留利润;(IC)约束表明φ型的零售商只有选择φ型的契约时其期望利润才是最大的. 首先考虑φ型零售商选择ψ型契约时其期望利润 E[Πr(φ,w(ψ),b(ψ),T(ψ),Qr)] -[w(ψ)-b(ψ)]Qr-T(ψ). (13) 记零售商承诺的最优订购量Qr(φ,ψ)∈argmaxΠr(φ,w(ψ),b(ψ),T(ψ),Qr),则 =w(ψ)-b(ψ). (14) 将式(14)代入式(13),得 令Qr(φ*)=Qr(φ,φ),当零售商真实的表露市场需求状态时,其期望利润为 (15) 由式(13)得 因此 (16) 结合式(15)和(16) 令Qm(φ*)=Qm(φ,φ)则制造商的期望利润 (17) 将式(17)代入式(A2)可得 其中 (18) (19) (20) +b*(φ). 通过以上计算可得命题2. 命题2 当需求类型φ是连续变量时,最优回购契约(w(φ),b(φ),T(φ))如下 b*(φ)=m, +b*(φ), -π0, (21) 注5 在连续的需求状态下,制造商为获取需求信息而向零售商所支付的信息租金为 并且,当b*(φ)→pr-cr时信息租金将为零. 命题3 在连续需求类型情形下,制造商的最优契约(w*(φ),b*(φ),T*(φ))可以使2个渠道达到协调,并且也可以使自己的信息租金为零. 命题4 无论是在离散需求类型还是在连续需求类型下,制造商均实现了集中式最优. 在双渠道供应链中,制造商无法直接从直销渠道获取需求信息,只能借助零售商对契约的选择间接获取有效信息,再将这一状态延伸至直销渠道,而传统渠道的零售商掌握着更多关于市场需求类型的信息.制造商为了从零售商那里诱取需求类型信息,建立了一组契约,此契约中包含回收价格,批发价格,转移支付三个变量.面对此契约零售商可灵活的应对不确定的需求,为此零售商获取的高于其保留利润部分的利润将会减少.与信息对称相比,制造商的利润有所减少,其减少量会以信息租金的形式转移到零售商一方.基于此得到了需求信息不对称下的最优回购契约,并且分析了此契约只能满足零售商的保留利润,而制造商夺取了零售商原本想高于其保留利润部分的利润,此时的解几乎可以被看作是第一最优解,也得到了无论是在离散还是连续的需求类型状态之下,作为政策的制定者,制造商均实现了集中式情形下的最优解. [1]MCAKANYILDIRIM,FengQI,XianghuaGAN,et al.Contractingandcoordinationunderasymmetricproductioncostinformation[J].ProductionandOperationsManagement. 2012, 21(2):345-360. [2]HengLIU,OOZER.Channelincentivesinsharingnewproductdemandinformationandrobustcontracts[J].EuropeanJournalofOperationsResearch. 2010, 207(3):1341-1349. [3]ECAO,YujieMA,CanWAN,et al.Contractingwithasymmetriccostinformationinadual-channelsupplychain[J].OperationsResearchLetters. 2013, 41(4):410-414. [4]VBABICH,HantaoLI,PRITCHKEN,et al.Contractingwithasymmetricdemandinformationinsupplychains[J].EuropeanJournalofOperationalResearch.2012, 217(2):333-341. [5]SMUKHOPADHYAY,DongqingYAO,XiaohangYUE.Informationsharingofvalue-addingretailerinamixdechannelhi-techsupplychain[J].JournalofBusinessResearch. 2008, 61(9):950-958. [6]XiaohangYUE,JLIU.DemandForecastSharinginadual-channelSupplyChain[J].EuropeanJournalofOperationsResearch. 2006, 174(1):646-667. [7]RuiliangYAN,ZhiPEI.Informationasymmetrypricingstrategyandfirm'sperformanceintheretailer-multi-channelmanufacturersupplychain[J].JournalofBusinessResearch. 2011,64(4):377-384. [8]DongqingYAO,XiaohangYUE,XiaoyinWANG,et al.Theimpactinformationsharingonareturnpolicywiththeadditionofadirectchannel[J].InternationalJournalofProductionEconomics. 2005, 97(2):196-209. [9]ChungchiHSIEH,ChenghanWU,YajingHUANG.Orderingandpricingdecisionsinatwo-echelonsupplychainwithasymmetricdemandinformation[J].EuropeanJournalOperationalResearch. 2008, 190(2):509-525. [10]QiangGONG.Optimalbuybackcontractswithasymmetricinformation[J].InternationalJournalofManagementandMarketingResearch. 2008, 1(1):23-47. [11]XianghuaGAN,SSETHI,JingZHOU.Commitment-penaltycontractsindrop-shippingsupplychainswithasymmetricdemandinformation[J].EuropeanJournalofOperationalResearch. 2010, 204(3):449-462. [12]TiaojunXIAO,DanqinYANG.Risksharingandinformationrevelationmechanismofaone-manufacturerandone-retailersupplychainfacinganintegratedcompetitor[J].EuropeanJournalofOperationalResearch. 2009, 196(3):1076-1085. [13]HeXU,NingSHI,ShihuaMA,et al.Contractingwithanurgentsupplierundercostinformationasymmetry[J].EuropeanJournalofOperationalResearch.2010, 206(2):374-383. Contracting with Asymmetric Demand Information in Dual-Channel Supply Chains YAN Rong-fang ,ZHANG Lai-jiang Based on the newsboy model, this paper studied the contract coordination of dual channel supply chain consisting of a manufacturer and a retailer in demand under the condition of asymmetric information. We modeled the retailer's private information as a space of either discrete or continuous demand states, and analyzed the optimal performance, the buyback contract coordination in supply chain. dual-channel supply chain; asymmetric information; return policies; supply chain coordination 2015-06-07 国家自然科学基金(71471148);甘肃省科技支撑计划项目(1104GKCA030) 颜荣芳(1964—),(1964-),男,甘肃武山人,教授,博士 E-mail:yanrf@nwnu.edu.cn F270.7 A

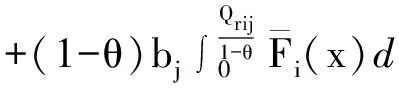
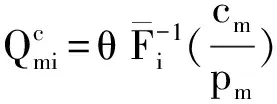


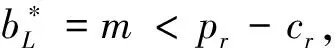







3 连续需求状态模型


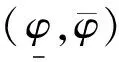





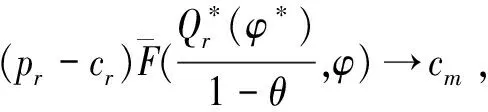



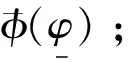
4 结束语
(College of Mathematics and Statistics, Northwest Normal University, Lanzhou ,Gansu 730070, China)
