刍议大学数学第一堂课的教学内容

王秋宝　王凡梅

摘要：从高中迈入大学课堂，大学生们的第一堂课绝大多数是数学课。本文针对这个现况，结合作者自身的教学实践以及数学课程本身的特点，探讨如何设置第一堂数学课的教学内容，做好初等数学和大学数学的无缝衔接。

关键词：初等数学 高等数学

高等数学和线性代数是大学本专科生的一门基础课，对于理工科学生来说这两门课程为后续课程的的学习提供必要的基础知识。而且，大多数学校开学第一堂课基本上都是数学课，因此，大学数学教师如何上好这第一堂课就显得尤为重要。

这些学生都是刚刚离开父母，来到一个全新的环境，对大学的学习都很懵懂。本人就从下面几个方面阐述一下大学数学教师堂课教学内容应该如何设置。

一、大学生活与中学生活

既然是第一堂课，就不要一上来就进入课程的学习。大学生活与中学生活完全不同，这里没有父母和班主任无微不至地管理，不能依赖他人。倘若新生不能很快地适应大学新生活，会影响到未来四年的学习状态和效果。作为新生见到的第一个教师，我们有责任告诉他们大学生活与中学生活的区别，让新生能够尽快地适应集体宿舍生活，适应百人以上的大课堂，适应自学自理等等；注意提醒学生尽早确立学习生活计划，长短计划结合；养成良好的学习生活习惯。在上课一开始教师以自己上大学的亲身经历去讲述其如何从懵懂到适应大学的生活，拉近师生距离，这样有利于在以后教学中消除距离感和抗拒感。

二、大学数学的重要性

接下来，要进入的就是课程本身。但不要急于进入课程的内容讲授。任何一门课程在学习之前，学习者都希望知道学习这门课程的原因。恩格斯在《反杜林论》中提出：“纯数学是以现实世界的空间形式和数量关系，也就是说，以非常现实的材料为对象的，这种材料以极度抽象的形式出现，这只能在表面上掩盖它起源于外部世界。”大学数学作为近代数学的重要组成部分，它仍然是源于我们的现实世界，尤其是物理世界，我们不能教学中脱离这个本质。大学数学在自然科学和社会科学诸多领域，如物理、化学、医学、工程技术、控制理论、及经济学等乎所有的分支中都有着广泛的应用。近几十年来， 随着网络技术和金融技术的迅速发展，使得社会上越来越需要将新理论方法应用到工程实践中的应用数学人才，这些问题都反映了大学数学学习的必要性和重要性。另外，教师在讲述大学数学的重要性之外，还可以从它的起源讲起，让学生了解数学的历史是非常重要的，从历史中自然而然就会洞悉大学数学的必要性和重要性。

另外，还可以在讲述中适当地添加数学家的有趣的故事，不仅能够吸引学生的注意力，还可以激发他们的学习兴趣。比如在教学实践中我就十分钟爱于讲述伯努利家族的数学故事，当学生听到这个故事的时候，在惊叹于这个传奇家族能够数学家辈出之余，心中都暗暗决心能够成为那样的人物，从学生的眼神中看到了我所期待的。再比如在讲授线性代数时，我经常会讲述伽罗华和阿贝尔的励志故事，学生从他们艰苦而又坚决的精神中能够得到较好地激励，迸发学习热情。

三、大学数学学什么

中学数学，也可以叫做初等数学研究对象主要是常量，大部分内容直观形象，易于接受。而到了大学数学，其研究的是变量关系，是运动的数学。很多内容十分抽象，逻辑性很强，比如高等数学里面接触到的极限这个概念十分抽象，很多学生在学习时都是似懂非懂。

在介绍完与中学数学的区别之后，教师就要对课程的主要内容进行大致概述。大学数学主要是两门课程：高等数学和线性代数。所以教师要针对不同的课程特点简单描述它的主要内容，切忌搬照目录。比如，对于高等数学上册就可以简而概之为一元函数微积分。

当然对于学习方法，教师也要交代清楚。如何做好预习，如何做好课堂笔记，如何课下复习，如何独立完成作业等。

四、如何引出课程

这一部分的教学内容设计是至关重要的，人们不习惯于没有头绪的学习，喜欢知道所学习内容的来龙去脉，尤其是新知识和头脑中固有的旧有何关联。数学课程的学习从小学就开始，到了大学还要继续学习。很多大学生不禁要问：“大学的数学和我学过的中学数学，甚至小学数学有什么关联？”

作为大学数学教师，对于学生的这一问题，教师要认真严谨地对待，不能使学生的数学知识出现断层。在前面，我们讲述过大学数学与中学数学的区别所在，这时候学生往往会错误的认为大学数学与中学数学是截然不同的两种数学。这个思想是十分危险的，其实，两者之间是一脉相承，对于数学课程的设置，是按照人类的认知规律的。在第一堂大学数学课中，我认为大学教师应该用90%左右的时间来阐述清楚这个问题，使得学生一开始就能够在头脑里建立一个知识脉络，等学完课程之后，学生能够自己梳理好知识体系。

在1900年的法国巴黎举行了跨世纪的国际数学家大会，在会上数学家庞加莱提出著名的二十三个数学问题，后来一个多世纪的数学发展都与这二十三个数学问题紧密相连。但我觉得更重要的是他本人在大会发言中的一句话：“数学中每一步真正的进展都与更有力的工具和更简单的方法的发现密切联着，这些工具和方法同时会有助于理解已有的理论并把陈旧的、复杂的东西抛到一边。数学科学发展的这种特点是根深蒂固的。”

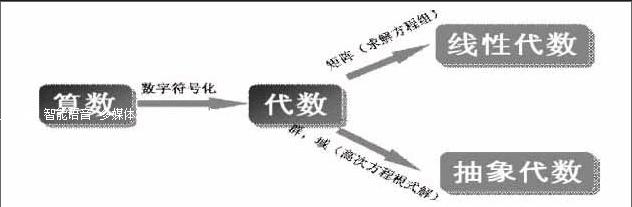
按照这种思想我们可以理清高等数学和线性代数与中学数学的关系。在讲授时，教师可以从最早小学的算术开始，数字符号化这个新方法把算术发展成中学代数，进一步矩阵这一新工具又将其发展成为线性代数。另一方面从平面几何开始，由于向量这一概念的提出，出现了解析几何，在求曲线切线的过程中，引入了极限的概念，进而引出高等数学中的微积分。

从这两种不同的课程的引入，学生可以在头脑里有一个很清晰的脉络。比如我在引入线性代数这门课程时就会写出下面的图示加以讲述。

五、小结

不同教学阶段如何衔接这是教学改革非常重要的一个话题，作为大学数学教师有义务在大学数学的第一堂课中重视衔接问题。按照本文所设计的教学内容教学，可以让学生对第一次课回味无穷，了解大学数学的课程特点，使学生知道为何学习，如何学习。教师也能够给学生留下美好印象，使学生从心里接受教师，从而建立和谐的师生关系。

参考文献：

[1]同济大学数学系编.高等数学（第六版）[M].北京：高等教育出版社，2009.

[2]吴文俊，龚昇.简明微积分读后感[J].数学通报，2000（1）.

（责编 张景贤）