基于PCA与RBF的建筑能耗预测建模

戴坤成， 王贵评， 赵 超

(福州大学石油化工学院， 福建 福州 350116)

基于PCA与RBF的建筑能耗预测建模

戴坤成， 王贵评， 赵 超

(福州大学石油化工学院， 福建 福州 350116)

由于建筑能耗因子间存在非线性和高度冗余特性， 传统预测方法很难消除数据之间冗余和捕捉非线性特征， 导致预测精度较低. 为了提高建筑能耗预测精度， 提出一种将主成分分析(principal component analysis, PCA)和径向基函数(radial basic function, RBF)神经网络相结合的建筑能耗预测方法(PCA-RBF). 利用PCA消除建筑能耗高维变量数据的相关性， 并按累积贡献率提取主成分， 将主成分作为RBF神经网络的输入进行训练学习. 通过PCA避免了模型过多的输入导致的训练耗时长及预测精度较低的不足. 通过将PCA-RBF模型方法应用于某办公建筑能耗的预测中， 并与RBF神经网络及BP神经网络模型相比， 实验结果表明PCA-RBF模型方法能有效提高建筑能耗预测精度.

建筑能耗； 主成分分析； RBF神经网络； 正交试验； 组合预测

0 引言

随着建筑能耗在我国能源消耗中的比重日益增长， 建筑节能受到全社会越来越多的关注. 准确有效地预测建筑能耗是进行建筑能耗分析及节能评估的重要基础， 也是建筑节能优化设计的主要依据[1]. 建筑能耗系统是由多因素组成的复杂系统， 单体建筑能耗与围护结构传热系数、 窗墙比、 体形系数、 遮阳系数、 室外温度及设备启停等因素之间存在复杂的非线性关系， 且各因素之间存在很强的相关性， 使得建立建筑能耗精确预测模型面临极大的困难.

人工神经网络因其具有强大的非线性映射和函数逼近能力， 目前已成为解决非线性动态系统建模问题的有效方法[2-7]. RBF神经网络作为近年来受到广泛关注的一种新型前馈神经网络， 因其具有结构简单、 收敛速度快以及推广能力强等特点， 已经广泛应用于建筑能耗建模与分析领域[8-10].

传统基于神经网络的建筑能耗预测方法是简单地把所有能耗影响因素或人为地将部分主要因素作为神经网络模型的输入. 尽管RBF神经网络具有强大的非线性映射能力和良好的泛化性能， 但是输入变量之间存在的强耦合、 非线性特性势必影响模型的精度和泛化能力. 因此需要寻找一种能够准确提取变量间重要信息的方法来消除变量之间的相关性， 从而有效提高建模精度， 降低计算复杂度.

主成分分析(PCA)是进行数据压缩和信息提取的一种有效方法[11]. 其主要思想是将由原始变量构成的高维数据空间投影到低维特征空间. 新特征空间的主元变量既保留了原始变量的主要信息， 又消去了变量间的冗余信息.

为了提高RBF神经网络建筑能耗模型的预测精度和模型泛化能力， 本文结合PCA的特征提取功能和RBF网络强大的函数逼近能力， 提出一种基于PCA和RBF神经网络的建筑能耗预测建模方法. 通过机理分析确定建筑能耗主要影响因素的基础上， 采用主元分析方法对输入变量进行特征提取， 消除输入变量之间的相关性， 将新的特征信息作为RBF神经网络的输入变量建立建筑能耗预测模型. 最后对某一办公建筑的能耗进行预测， 并与BP网络、 RBF网络的预测结果进行比较， 结果表明PCA-RBF预测模型的性能优于其它两种预测模型.

1 主元分析

PCA作为输入数据降维和揭示变量间线性相关关系的一种统计相关分析技术， 从可观测的显式变量中提取信息， 组成不可直接观测的隐含变量， 在保证信息数据丢失最少原则下对高维变量空间进行降维， 达到消除冗余信息的目的. PCA的主要步骤如下：

设有样本数据集X=[x1,x2, …,xn]，xk=[x1,x2, ...,xf]T，k表示样本序号，f表示维数；λ1≥λ2≥…≥λf≥0为协方差矩阵V的特征根；L=[L1,L2, …,Lf]，Li=[γ1i,γ2i, …,γfi]T是与λi对应的协方差矩阵V的单位正交特征向量， 则样本数据X的第i个主元成分Yi可表示为：

确定主元个数t的方法可以用经验法， 即取最小的t使得：

式中:η为常数， 一般取η=0.9， 即保证前t个主成分的累积贡献率超过90%.

2 径向基函数神经网络

RBF神经网络由输入层、 隐含层和输出层3层组成[12-13]. 输入层节点只传递输入信号到隐含层； 非线性隐含层节点一般由辐射状的作用函数构成， 径向基函数通常采用高斯函数； 线性输出层作用函数通常选取线性函数， 网络的输出为隐含层节点输出的线性加权和. 本文RBF神经网络隐含层节点的径向基函数采用高斯函数， 隐含层第l神经元的转换函数为：

式中:Y为输入矩阵向量；cl和σl分别为高斯函数中心和宽度. 输出层输出如下：

式中:Zp表示第p个网络输出值；Wp为输出层神经网络的阀值；Wlp为输出层神经网络的权值；q为隐含层节点数.

3 基于PCA-RBF的建筑能耗预测方法

3.1 输入参数的选择

在应用神经网络建立建筑能耗预测模型过程中， 首先需要对影响建筑能耗的因素进行分析， 选择对期望能耗影响较大的一些因素， 组成预测模型的有效输入变量集. 影响建筑能耗的因素众多， 主要包括外部条件、 建筑构造和室内条件三个方面[14-15]：

参考相关文献， 本文最终选取最低照度(x1)、 灯光热扰(x2)、 室外干球温度(x3)、 室外相对湿度(x4)、 设备热扰(x5)、 电热转换率(x6)、 人均新风指标(x7)、 家具系数(x8)、 外墙传热系数(x9)、 内墙传热系数(x10)、 玻璃遮阳系数(x11)、 玻璃传热系数(x12)、 通风次数(x13)13个参数作为能耗模型的输入参数.

3.2 建模步骤

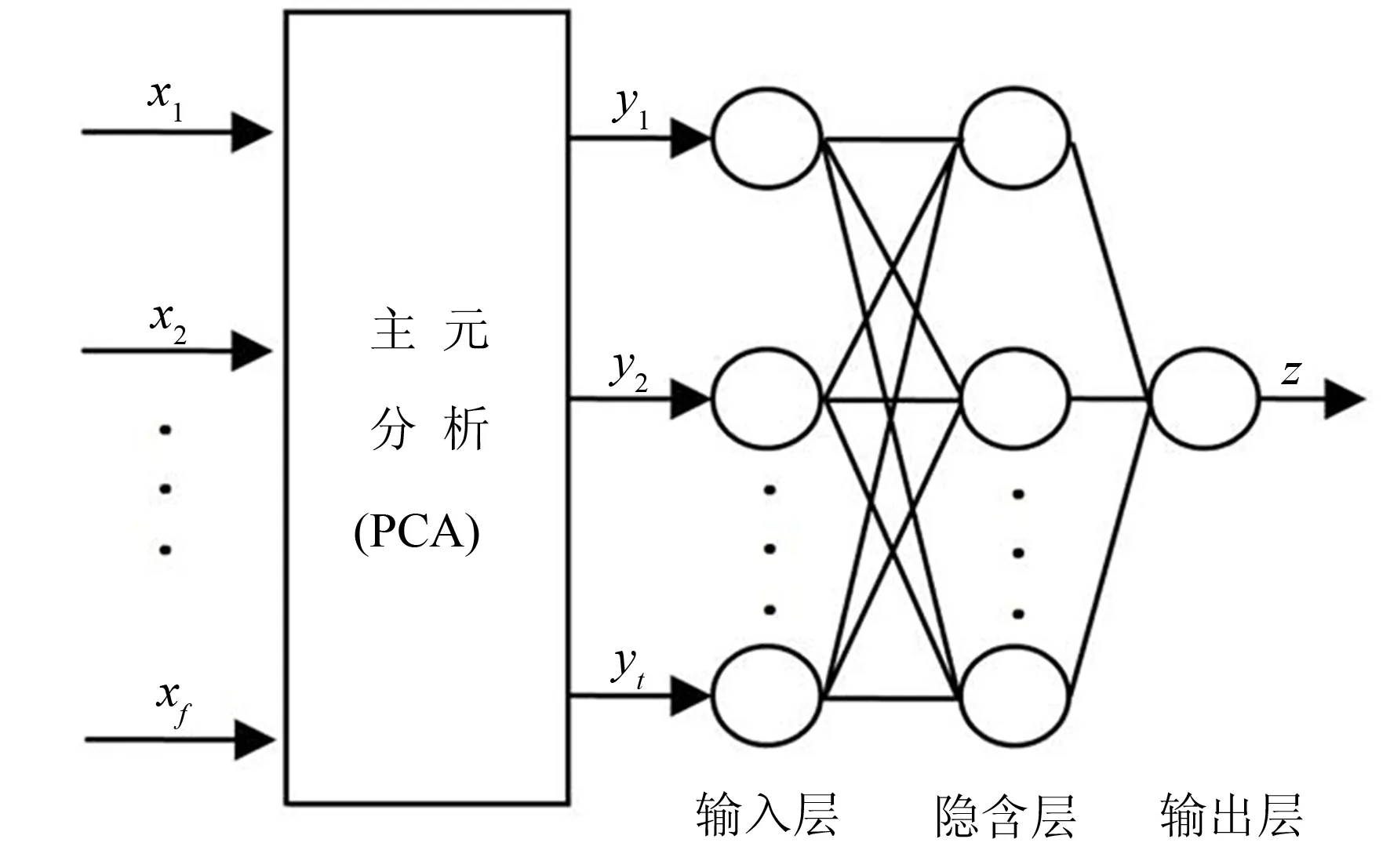
图1 PCA-RBF预测模型结构图 Fig.1 Structure of the predictive model based on PCA and RBF

为了提高RBF神经网络建筑能耗模型的预测精度和模型泛化能力， 采用主元分析方法对RBF网络输入变量进行特征提取， 将特征提取后的主元作为网络新的输入， 建立建筑能耗预测模型， 模型结构如图1所示.

基于PCA-RBF建筑能耗预测建模关键步骤可描述如下：

1) 数据归一化处理. 根据式(5)对数据进行归一化处理， 有T=[T1,T2, …,T13].

(5)

式中:xi(k)为建筑能耗影响因素xi第k个样本的采样值，Xi-max、Xi-min为影响因素xi的最大值和最小值；Tmax、Tmin为归一化的最大值和最小值， 取Tmax=1、Tmin=-1.

2) 提取样本主元. 根据第2节所提的PCA方法提取样本数据主成分， 并保证主成分累积贡献率超过90%.

3) 建立RBF神经网络模型. 以PCA提取的主成分数据作为RBF神经网络的训练样本数据， 采用K-均值聚类法确定网络中心， 使用最小二乘法确定网络权值， 建立RBF神经网络建筑能耗模型.

4) 采用测试集的数据检验所建立的RBF神经网络模型的预测效果， 若预测结果不满意则返回步骤3)重新训练网络.

4 案例分析

4.1 建筑简介

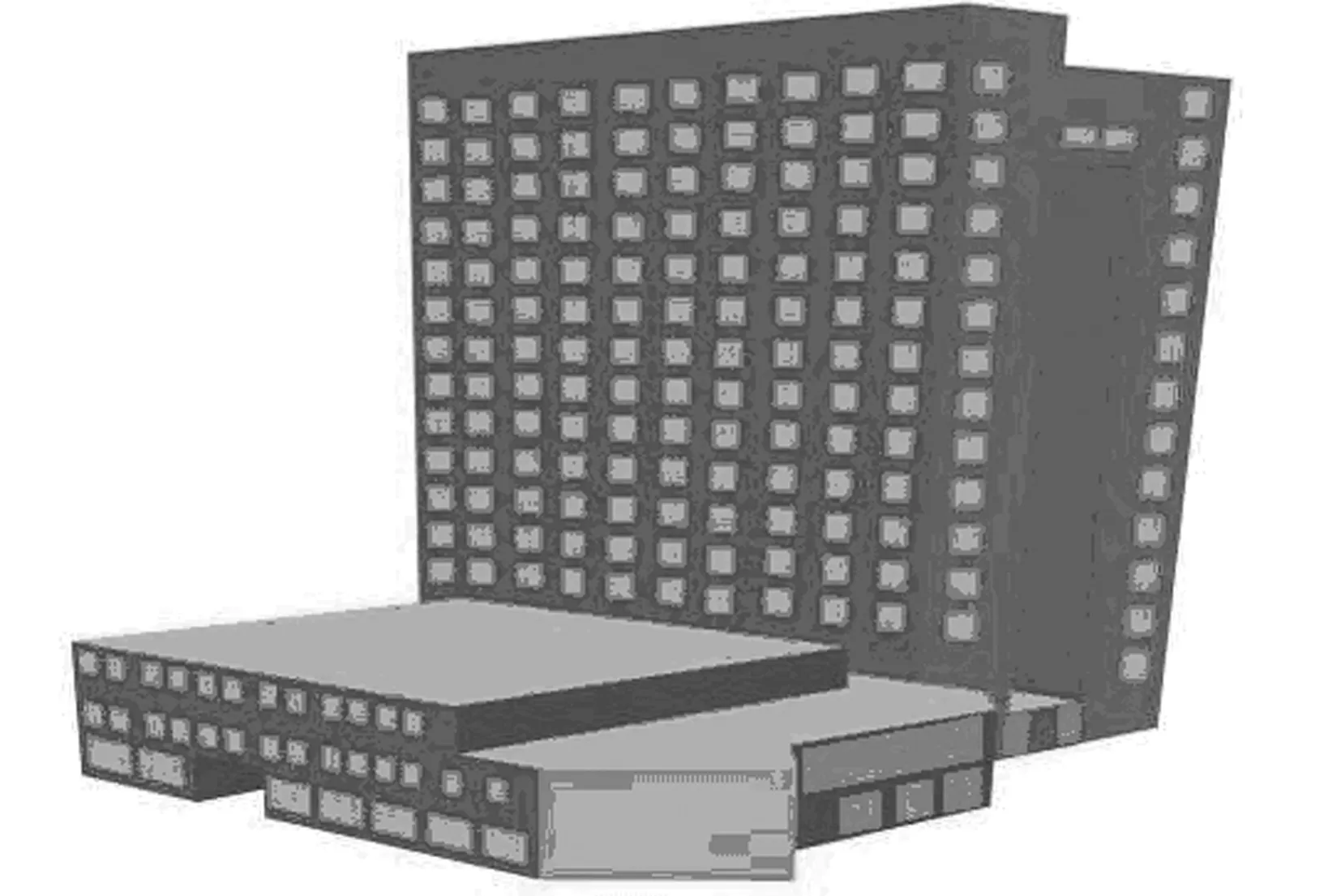
图2 办公建筑外形示意图 Fig.2 Shape of office building

用于验证本文所建立的PCA-RBF建筑能耗预测模型的建筑是国内某地区的一栋办公建筑， 该建筑为东西朝向的高层现浇钢筋混凝土框架-筒体结构建筑， 建筑外形示意图如图2所示.

建筑总高度为57.4m， 主楼地上16层， 地下1层， 附楼(裙房)三层. 总建筑面积为19 700.5m2. 地上建筑面积17 315.62m2， 地下建筑2 384.88m2， 标准层层高3.5m， 外窗尺寸为2.5m×2.0m， 窗台离地高度0.8m. 地下室砖墙为普通实心砖墙， 地上建筑砖墙厚度均为190mm， 实际墙厚200mm. 外墙开窗比例约为0.23， 无外遮阳， 设室内窗帘. 空调运行时间为8:00到17:00， 总计每天运行9h， 空调季为6月1日到8月30日.

4.2 评价指标

为了从整体上评价预测模型的预测精度和稳定性， 采用相对误差最大值Emax、 相对误差平均值Eave和均方根误差RMSE三个性能指标对预测模型进行评估.

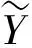
相对误差最大值Emax反映了预测值与期望值的最大偏离程度； 相对误差平均值Eave反映了预测值与期望值之间误差的大小； 均方根误差RMSE反映了误差分布的离散程度， RMSE越大， 误差序列越离散， 预测效果越差. 三个指标Emax、Eave、 RMSE都是越小说明预测效果越好.

4.3 构造样本集

为减少试验次数， 并保证试验的全面性， 本文采用正交试验方法获取数据样本集. 在仿真模拟过程中按照GB50189-2005《公共建筑节能设计标准》进行节能参数设置， 室外干球温度、 太阳辐射等其他参数选用历史平均水平. 影响因子的取值， 采用事先设定好的水平值， 每个因子选取3个水平值， 选用L27(313)正交表进行试验计算[16]. 为获得较为理想的训练数据， 本文进行四组正交试验， 经DeST-C计算获108组实验数据， 随机取其中的3/4作为训练样本， 余下的1/4作为测试样本验证模型的预测性能.

4.4 模型训练

首先对样本数据进行主元分析， 计算得到的碎石图如图3所示. 由图3可知， 当主成分个数为4时，η≥0.9之后， 将这4个主元作为RBF神经网络的输入样本以进行学习训练， 获得RBF神经网络预测模型.

应用训练后的预测模型对训练样本进行检验， 拟合结果如图4所示. 图4中菱形和方形标记基本重叠在一起， 这表明所建立的PCA-RBF模型对学习样本具有很好的拟合精度.

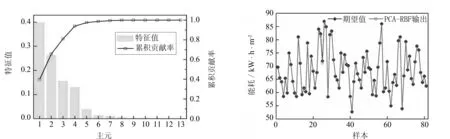
图3 主成分碎石图

4.5 结果分析

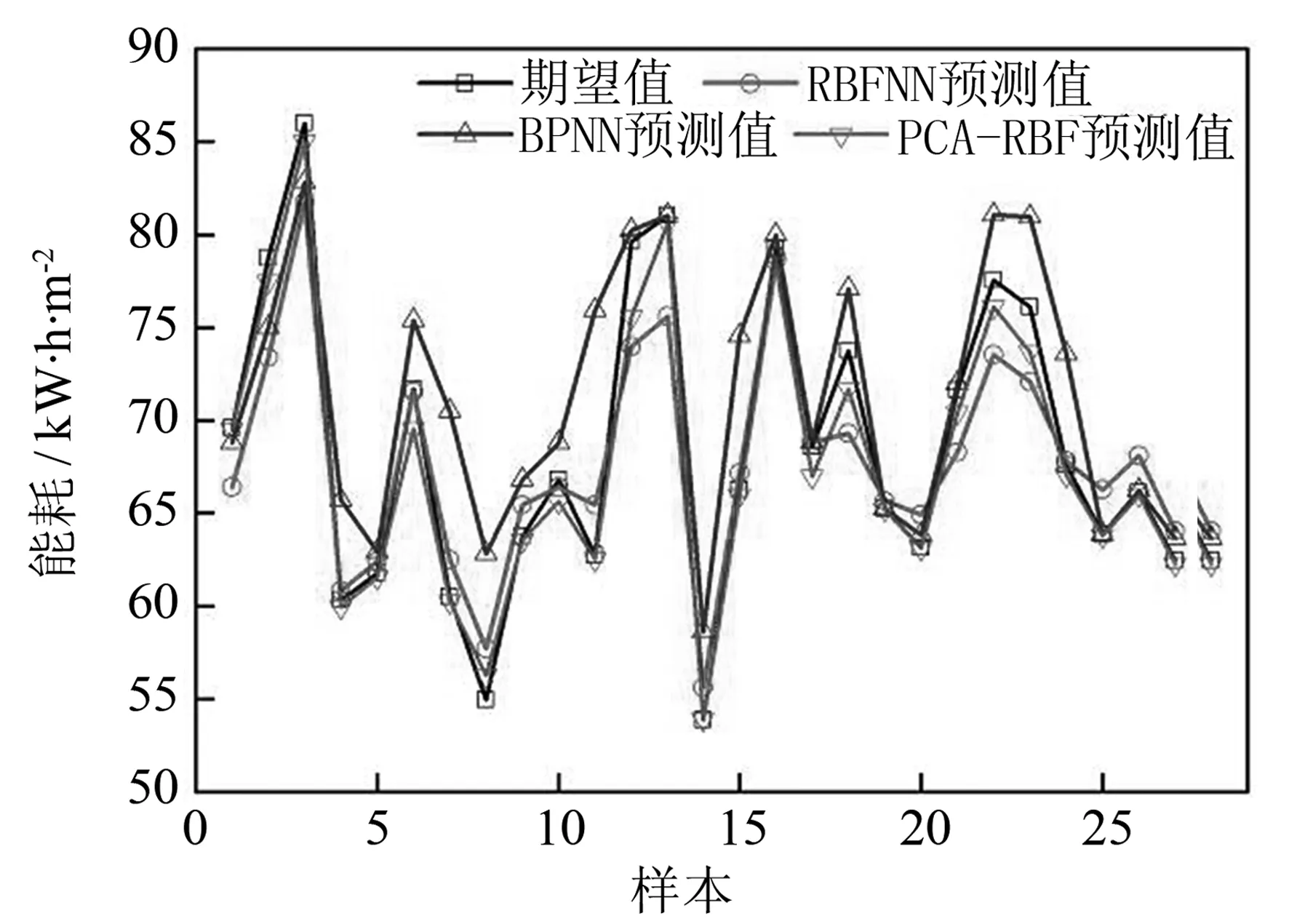
图5 模型预测比较Fig.5 Comparison of models prediction

应用PCA-RBF模型对27组测试样本进行预测， 并与单一的RBF神经网络和BP神经网络预测结果进行对比. 该办公楼建筑能耗的PCA-RBF模型、 RBF神经网络模型、 BP神经网络模型的预测输出曲线如图5所示.

为从整体上评价两种预测模型的预测精度和稳定性， 根据式(6)、 (7)、 (8)计算预测结果的相对误差最大值Emax、 相对误差平均值Eave和均方根误差RMSE， 计算结果如表1所示：

由表1可以看出， PCA-RBF组合模型预测结果的均方根误差为3.56， 比BP神经网络的29.22和RBF神经网络的9.13都要小， 这表明组合模型预测

方法减小了预测数据的波动幅度， 提高了预测数据的稳定程度， 并且预测精度也有所提高， 其相对误差平均值为1.43%， 也小于BP神经网络的5.84%及RBF神经网络的3.03%. 分析其原因， 主要是通过主元分析剔除了冗余信息， 并且只用少数变量就可以表示多个过程变量的动态信息， 不仅减少了网络的输入数， 同时主元变量之间的不相关性也使得网络的学习性能进一步增强. 正是结合了主元分析和RBF神经网络预测的优点， PCA-RBF模型的预测能力明显优于单一的RBF网络， 其预测精度和稳定程度均有所提高.

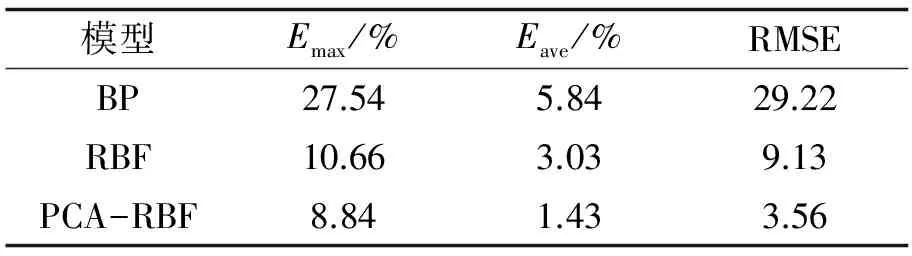
表1 三种模型预测结果比较

5 结论

1) RBF神经网络模型具有良好的全局逼近能力、 结构紧凑、 收敛速度快等优点， 因此本文在RBF神经网络的基础上建立建筑能耗预测模型， 能够较准确地对建筑能耗进行预测.

2) 提出PCA-RBF组合模型， 结合主元分析降维、 去相关的优点， 进一步提高了RBF神经网络对过程数据变化的适应能力. 本文所提方法预测结果的相对误差平均值Eave和均方根误差RMSE是RBF神经网络的40%左右， 表明PCA-RBF预测方法有效地提高了网络模型的学习效率和预测精度， 具有更好的泛化能力， 有着很好的推广应用前景.

3) PCA-RBF组合方法在建筑能耗预测中的应用， 为建筑物能耗的预测提供了一种新的方法， 为实现节能建筑奠定了基础， 便于提高建筑能耗系统的能源利用效率、 挖掘节能潜力.

[1] 陈改芳.重庆市公共建筑能耗模拟与节能研究[D]. 重庆: 重庆大学, 2007.

[2] 陈兴权, 王解先, 古川. 基于主成分分析的BP神经网络在形变预测中的应用[J]. 大地测量与地球动力学, 2008, 28(3): 72-76.

[3] 谢艳群, 李念平, 陈淑琴. 长沙市居住建筑能耗调查及偏相关性分析[J]. 煤气与热力, 2007, 27(5): 85-88.

[4] 严智勇, 许巧玲. 福州地区大型办公建筑能耗的多元线性回归分析[J]. 能源与环境, 2009(1): 51-52.

[5] 张伟. 基于季节灰色预测理论的公共建筑节能领域能耗监测研究[D]. 石家庄: 河北工业大学， 2010.

[6] 曹双华, 曹家枞. 基于神经网络的空调负荷混沌优化预测[J]. 东华大学学报, 2003, 29(1): 52-56.

[7] Curtiss P S. Energy management in central HVAC plants using neural networks[J]. ASHARE Trains, 1994, 100(1): 476-493.

[8] 李琼, 孟庆林. 基于 RBF 神经网络的建筑逐时空调负荷预测模型[J]. 华南理工大学学报: 自然科学版, 2008, 36(10): 25-30.

[9] 杨丹. RBF神经网络预测水泥水化热研究[J]. 国防交通工程与技术, 2011, 9(3): 31-33.

[10] Lyu Shiqin, Wu Can, Zhang Sufang. Application of the RBF method to the estimation of temperature on the external surface in laminar pipe flow[EB/OL]. (2013-09-02)[2014-05-13]. http://dx. doi. org /10. 1155/2013/205169.

[11] Xie Xiaodan, Xia Bin, Yu Jun. A comprehensive evaluation method based on PCA and BP neural network[C]//2012 Fifth International Conference on Information and Computing Science. Liverpool: IEEE, 2012: 71-74.

[12] MATLAB中文论坛. MATLAB神经网络30个案例分析[M]. 北京: 北京航空航天大学出版社， 2010.

[13] 丛爽. 面向MATLAB工具箱的神经网络理论与应用[M]. 合肥: 中国科学技术大学出版社， 2009.

[14] 魏鋆, 吴金顺, 张维亚, 等. 基于正交实验方法对建筑围护结构能耗的因素分析[C]//杜修力. 低碳经济与土木工程科技创新: 2010 中国国际建筑科技大会论文集. 北京： 科学出版社， 2010.

[15] 王乾坤, 万畅. 公共建筑围护结构对建筑能耗的影响分析[J]. 武汉理工大学学报, 2011, 33(3): 112-115.

[16] 安秋香. 上海市高层办公建筑空调能耗现状及其影响因素研究[D]. 上海: 同济大学, 2004.

(责任编辑： 林晓)

A prediction model for energy consumption of building based on PCA and RBF

DAI Kuncheng， WANG Guiping， ZHAO Chao

(College of Chemical Engineering， Fuzhou University， Fuzhou， Fujian 350116， China)

There are highly redundant features in affecting factors of building energy consumption, and the traditional method has low predictive accuracy. In order to improve the accuracy of building energy consumption forecasting, a model method for energy consumption based on principal component analysis (PCA) and radial basic function (RBF) neural network is proposed, which combines the abilities of PCA to de-correlate the variables and reduce the dimensionality of the data with that of neural network to approximate any complex nonlinear function. The PCA-RBF model is applied to the energy consumption prediction for an office building, and the simulated results show that the PCA-RBF has better accuracy compared with RBF neural network model and BP neural network model, which is considered that the PCA-RBF is effective for building energy consumption prediction.

energy consumption of building； principal component analysis； RBF neural network； orthogonal experiment； combination predicting

10.7631/issn.1000-2243.2015.04.0512

1000-2243(2015)04-0512-05

2014-10-14

赵超(1976-)， 副教授， 主要从事过程控制和能源优化研究， seasky76@163.com

国家自然科学基金资助项目(60804027， 61374133)

TU111

A