路内停车对交通流的影响分析
2015-06-01韦兰香梁玉娟钟友坤
韦兰香, 梁玉娟, 钟友坤
(河池学院 物理与机电工程学院, 广西 宜州 546300)
路内停车对交通流的影响分析
韦兰香, 梁玉娟, 钟友坤
(河池学院 物理与机电工程学院, 广西 宜州 546300)
针对带有路内停车带的单向单车道上车辆的行为过程建立车辆元胞自动机行为规则,并数值模拟周期边界条件下道路上待停车辆的比例系数f和路内停车行为造成对后车的阻碍时间T对道路交通的影响。研究结果表明,f和T对道路交通的影响很大。
路内停车带;交通流;单向单车道;元胞自动机
0 引言
进入21世纪以来,我国经济持续高速增长,城市化、工业化进程显著加快。随着人们物质生活水平的提高,越来越多的私家车进入了普通家庭,近几年来增长速度尤其迅猛。虽然机动车给人们的出行带来了方便,却面临着越发突出的“停车难”问题。目前,我国许多城市因停车用地太少,路外停车设施严重短缺,停车泊位不能满足现实需要,而普遍采用路内停车方式来停车。路内停车通常占用一部分机动车道、慢车道(或巷道)或人行道。其具有停车方便、周转快等优点,因此利用率较高。但另一方面,路内停车削弱了道路的通行能力,降低了车辆的行驶速度。
元胞自动机交通流模型是定义在一个由具有离散、有限状态的元胞组成的元胞空间上,并按照一定的局部规则,在离散的时间维度上演化的动力学系统[2]。其强大的复杂计算功能、固有的并行计算能力、高度动态特征以及高度灵活性等特征,使得它在模拟复杂的交通运输系统的时空动态演变方面具有强大的能力[3],而NaSch模型是最重要的一维元胞自动机交通流模型之一。
为了讨论路内停车对交通流的影响,本文以NaSch模型为基础,建立带有路内停车带的路段上车辆的交通流模型并用计算机进行数值模拟,观察不同参数设定情况下交通流特性的变化特征[1],从流量—密度、速度—密度基本图和时空演化斑图来对比分析道路上待停车辆的比例系数、车辆停车过程对后车造成的阻碍时间对道路交通的影响。
1 模型的建立
图1是一典型的路内停车路段示意图,图中路段为单向单车道,路侧有停车带。路段中有行车道和停车带,其中A为行车道上的车辆,B为停车带上的车辆。

图1 带有路内停车带的单向单车道路段示意图
在本文中,路段模型示意图如图2所示。用一个一维点阵代表一条单车道,即行车道由1 000个元胞构成,道路长度为L,每一个元胞对应的实际道路长度为7.5 m。每一个元胞在每一时刻处于空闲或容纳一辆车的状态。行车道上的车辆自左向右行驶,有斜线的元胞为容纳一辆车的状态,空白元胞为空闲状态。第530个元胞为正在停车车辆的位置Lb,第600个元胞为路内停车带的终止位置Ls。Ld为路内停车带的起始位置,La为停车带的长度。系统采用周期性边界条件,从左向右行驶车辆,当驶出右边界后,从左边界重新进行[1]。路段中只有一部分区域设有路内停车带。停车带也由元胞构成,灰色元胞为停有一辆车的状态,空白元胞为空闲状态。
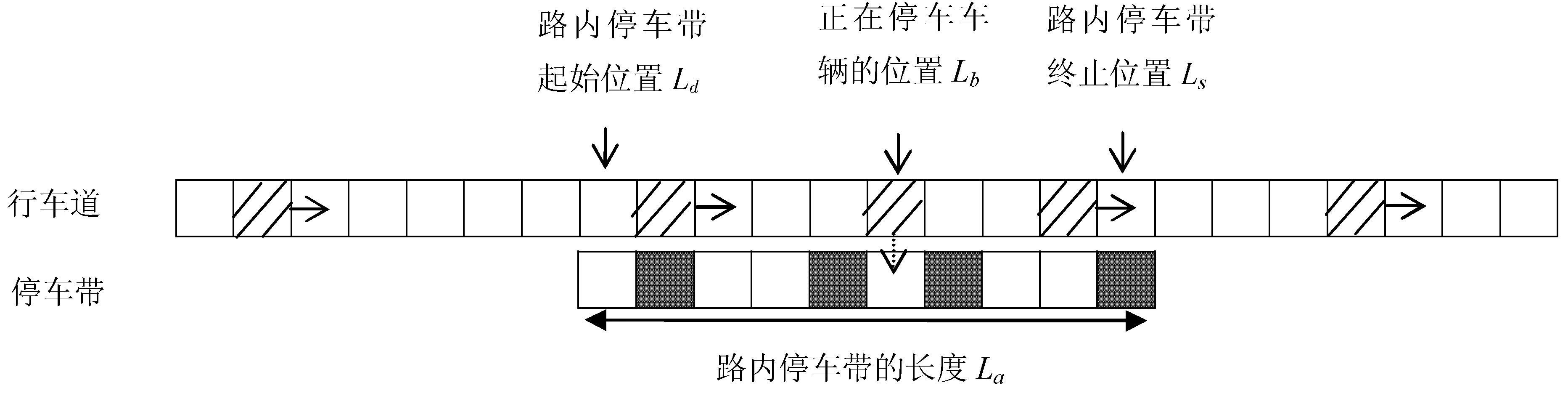
图2 带有路内停车带的路段模型示意图
假设行车道上有不停车辆和待停车辆,每辆车均占一个元胞,每一辆车的状态由该车的速度v来表示,v∈[0,vmax],即速度可在0与最高车速之间取其中一值,取vmax=3 cell/s(每秒3个元胞)。vn(t)和xn(t)分别为车道上第n辆车在t时刻的速度和位置,xn+1(t)则是车道上第n+1辆车在t时刻的位置,gapn(t)=xn+1(t)-xn(t)-1是t时刻第n辆车与前方紧邻车辆之间的元胞数,亦为待停车辆与前车的距离。ts为停车等待时间的积累。在实际的交通中,车辆在进行侧方位停车时,要耗费一定的时间,为了便于分析,停车车辆在停车时速度取0。
1.1 不停车辆的运行规则
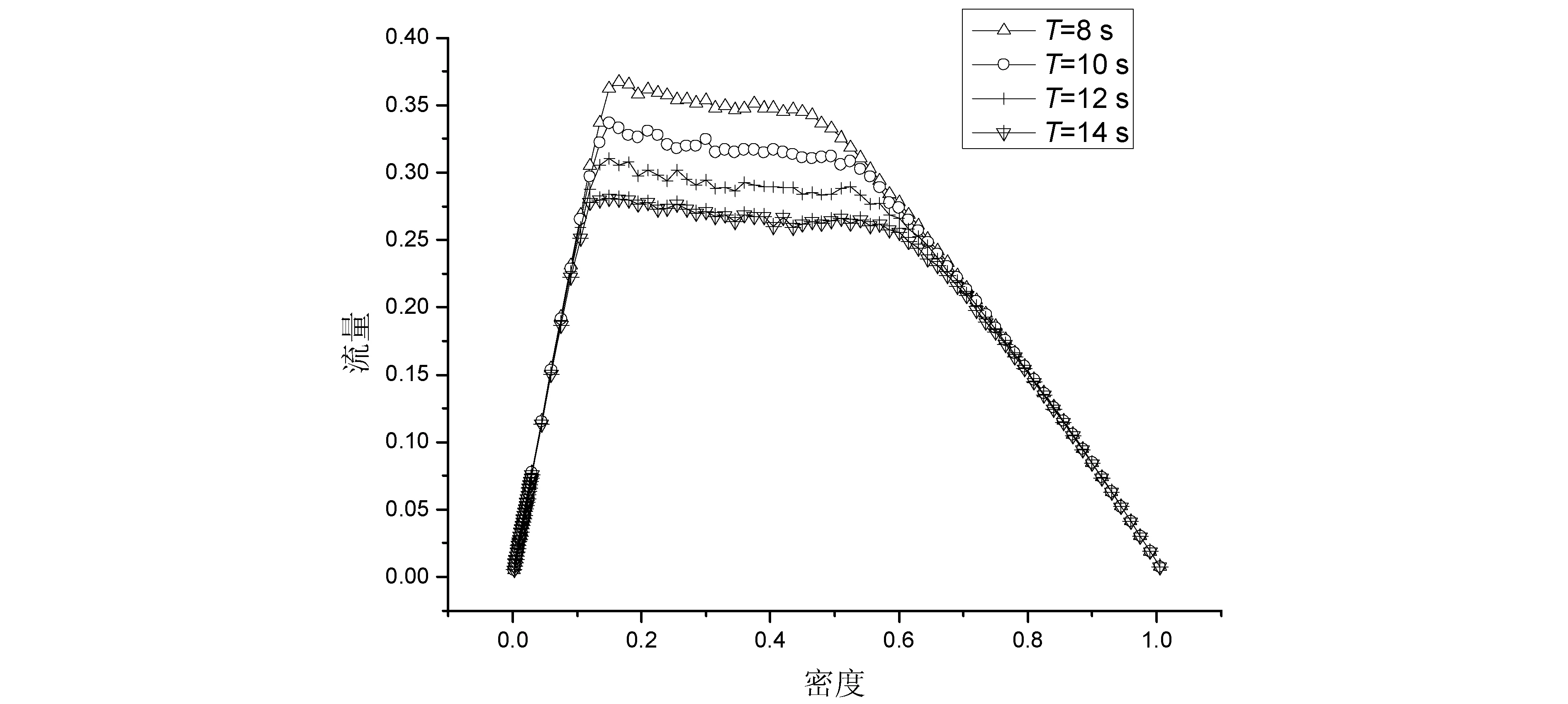
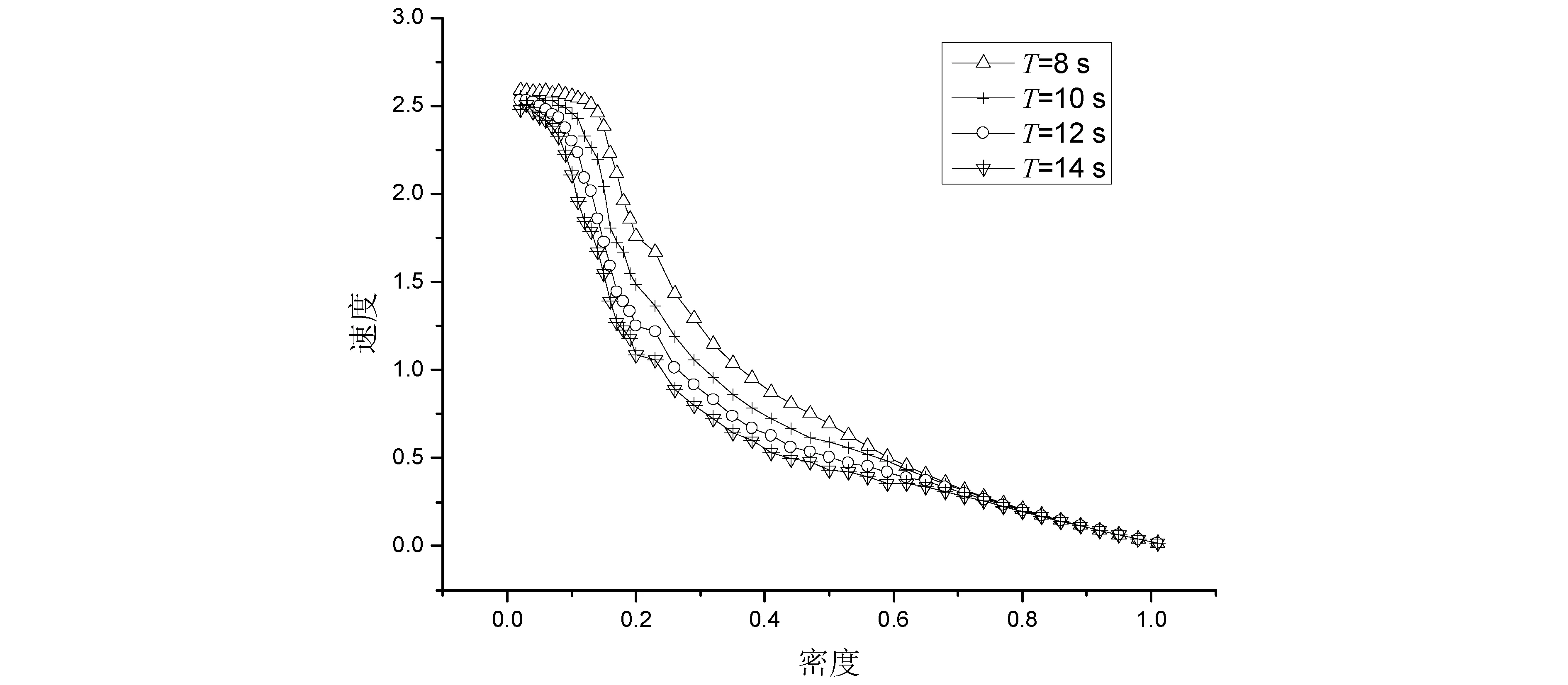
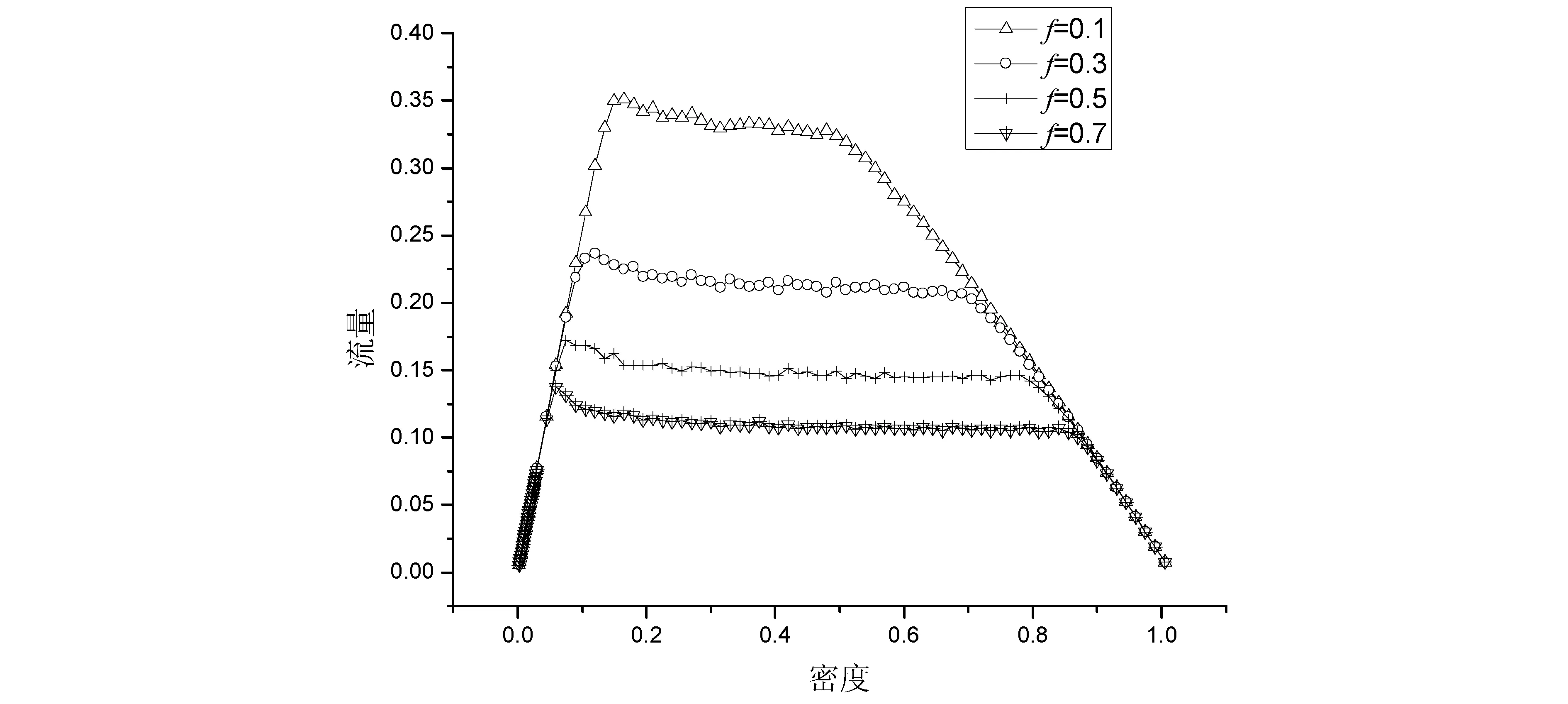
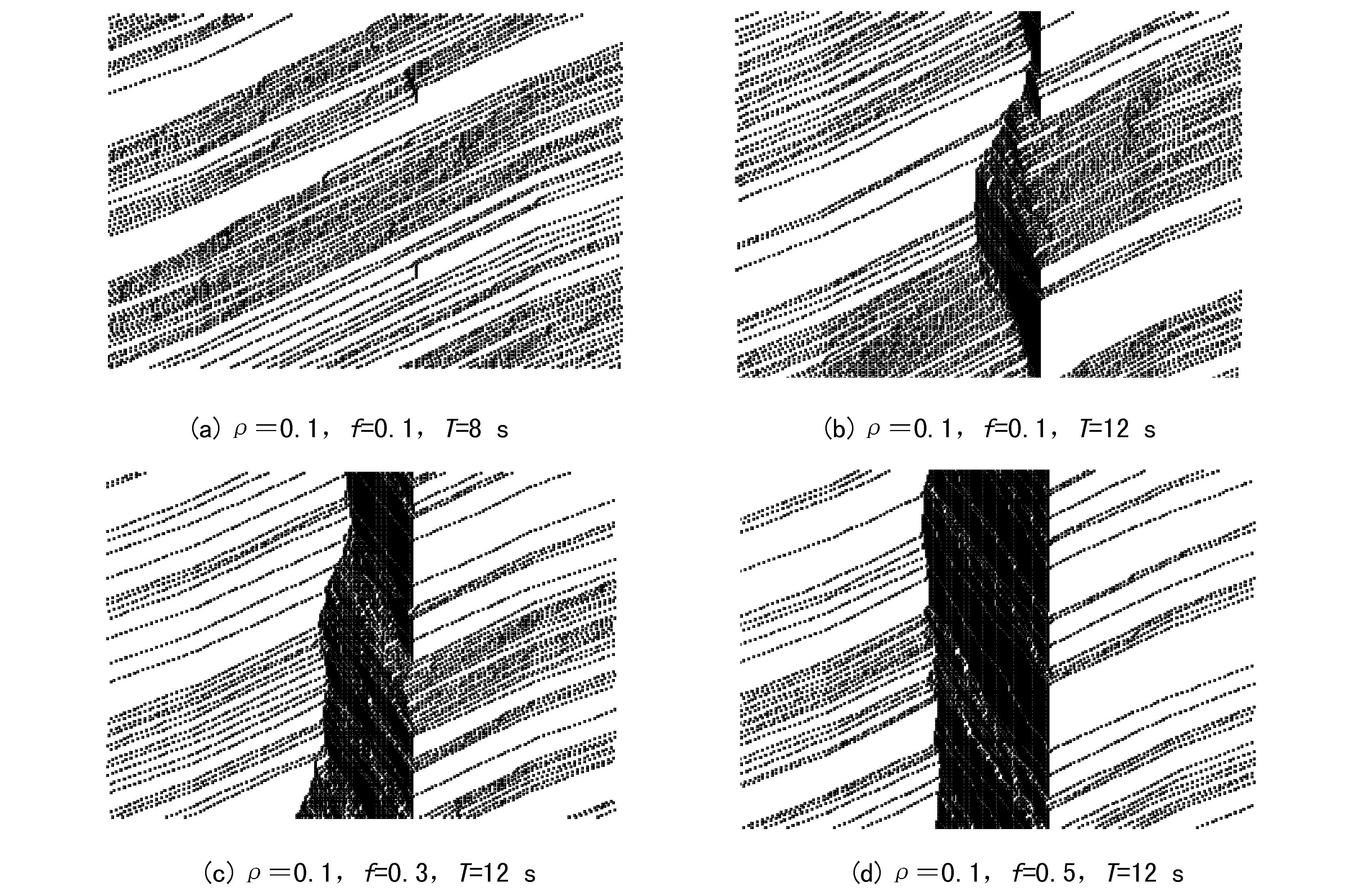
当不停车辆来到停车区附近时,其运行规则为:(1)若前方无车辆正在停车,则按NaSch模型规则运行;(2)若发现前方有车辆正在停车,则必须停车等待。即,若(xn(t)=Lb且ts 1.2 待停车辆的运行规则 当待停车辆来到停车区附近时,其运行规则为:(1)若前方无停车位,则其运行规则与不停车辆相同;(2)若发现前方有停车位,则减速停车。这里判断有停车位的条件是gapc(t) 1.3 修正NaSch模型的演化规则 本文对NaSch模型进行一些修改,即在其演化规则的基础上,加上了确定车辆的延迟概率这个规则。本文中修正的NaSch模型的演化规则表示为: (1)确定车辆的延迟概率P: 在带有路内停车带的路段上行驶的车辆,延迟概率取较大值P0=0.8,其他情况下,取较小值P=0.25; (2)确定性加速过程:vn(t)→min(vn(t)+1,vmax); (3)确定性减速过程:vn(t)→min(vn(t),gapn(t)); (4)以概率P随机减速过程:vn(t)→max(vn(t)-1,0); (5)位置更新过程:xn(t)→xn(t)+vn(t)。 在数值模拟的时候,计时开始时,让车辆以一定的比例,以一定的车辆密度ρ随机分布在一维1000个元胞链L上,其中待停车辆占总车辆的比例为f。每一次运行取40000时间步进行数值模拟,为消除暂态的影响,开始的20000时间步不进行统计,以后的20000时间步的每一时间步对速度νn(t)进行统计,而每一次运行的平均速度就是将经过20000时间步的速度对时间求平均。考虑到存在随机问题,为减小随机误差,总共运行10次,再对10次运行取平均值。 在各种路内停车方式中,用时最长的是侧方位停车方式,对道路交通造成的影响也最大。以该方式进行停车时,车辆在停车位一侧停留一段时间后才进入停车位,而这一段时间就是待停车辆对后车的阻碍时间。在实际的交通中,不同的驾驶员、不同的道路车流状况、不同的路内停车带的位置及设计等因素,都会造成车辆在停入泊位过程中对后车的阻碍时间不同。我们在日常驾驶车辆进行侧方位停车实验和测量时发现,阻碍时间为8 s到15 s不等。因此,在进行数值模拟时,由于停车而对后车造成的阻碍时间T在8 s到15 s之间取值。 为了研究周期边界条件下的路内停车对交通流的影响,通过取定道路车辆的密度ρ,改变待停车辆比例系数f和改变车辆停车过程对后车造成的阻碍时间T的方式进行数值模拟,通过流量—密度、速度—密度基本图和时空演化斑图来进行分析讨论。 2.1 对流量—密度和速度—密度基本图的分析讨论 2.1.1 停车过程对后车造成的阻碍时间T对交通流的影响 取定待停车辆的比例系数为f=0.1,改变阻碍时间T进行数值模拟,得到的流量—密度基本图和速度—密度基本图如图3、图4所示。 图3 不同阻碍时间T的流量—密度基本图(P0=0.8,P=0.25,f=0.1) 图4 不同阻碍时间T的速度—密度基本图(P0=0.8,P=0.25,f=0.1) 图3显示,模型在P0=0.8,P=0.25,f=0.1时,车辆密度很小的时候,流量随着密度线性增加;当中密度时,流量随密度的变化关系出现了一个流量不随密度变化的平台区域;而在密度很大的时候,流量随着密度的增大线性减小。这样的模拟结果与实际交通情况是吻合的。因为,道路车辆的密度很小的时候,车辆数目少,车辆之间的相互影响小,车辆处于自由行驶状态,平均速度大,对应的流量也大;当中密度时,道路上出现的车辆数目增多,车辆之间的相互影响增大,平均速度减小。这时基本图上呈现流量变化很小的低速状态,即出现了一个平台区域,且平台范围所对应的密度约在0.1~0.6之间,而从图4对比可看出,在此密度区间的速度约为2.0~0.5,车辆出现了拥堵。当密度很大时,车辆数目很多,车辆之间的相互影响也变得很大,由于相互制约,车辆的平均速度急剧下降,这时又因受到停车时间的影响,车辆的速度更小了,导致流量也很快下降。 从图3中还可以发现:T的取值对模拟道路的通行能力影响非常大。车辆流量的大小因取定待停车辆的比例系数f而取决于停车车辆对后车的阻碍时间T的大小。随着阻碍时间T的增加,车辆在前进过程中受阻程度随之增大,对应的最大流量值逐渐减小。如图3,当阻碍时间为8 s、10 s、12 s、14 s时,对应的最大流量值分别约为0.37、0.33、0.30、0.28。 从图4中可看出,由于研究的车辆是在单向单车道上行驶的,而且车辆停车过程要耗费一定的时间,若是车辆正在进行路内停车行为时,其后正在行驶的车辆就必须减速甚至停车等待,使得道路上车辆的平均速度下降很快。随着停车车辆停车过程对后车造成的阻碍时间T的增加,平均速度下降得更多。此外,随着车辆密度的增加,平均速度均趋向于0,这样就出现了交通堵塞,造成道路通行能力的下降。 2.1.2 待停车辆的比例系数f对交通流的影响 取定停车过程对后车的阻碍时间为T=10 s,改变待停车辆的比例系数f进行数值模拟,得到的流量—密度基本图和速度—密度基本图如图5、图6所示。 图5 不同待停车辆的比例系数f的流量—密度基本图(P0=0.8,P=0.25,T=10 s) 图6 不同待停车辆的比例系数f的速度—密度基本图(P0=0.8,P=0.25,T=10 s) 图5显示,车辆密度很小的时候,流量随着密度线性增加;在中密度时,流量随密度的变化关系也出现了一个流量不随密度变化的平台区域;而在密度很大的时候,流量随着密度的增大线性减小。出现这样的结果是因为,道路车辆的密度很小的时候,车辆数目少,车辆之间的相互影响小,车辆处于自由行驶状态,平均速度大,对应的流量也大;在中密度时,道路上出现的车辆数目增多,车辆之间的相互影响就增大了,相比图6可看出,车辆平均速度减小,这时不能保持自由的行驶状态,而是出现拥堵,即出现了阻塞相;当密度很大时,车辆数目很多,车辆之间的相互影响也变得很大,由于相互制约,车辆的平均速度急剧下降,这时又因受到停车时间的影响,车辆的速度更小了,导致流量也很快下降。 从图5中还可以发现:f的取值对模拟道路的通行能力影响非常大。车辆流量的大小因取定阻碍时间T而取决于待停车辆比例系数的大小f。随着待停车辆比例系数的增加,车辆在前进过程中受阻程度随之增大,对应的最大流量值逐渐减小。如图5,当待停车辆占总车辆数的10%、30%、50%、70%时,对应的最大流量值分别约为0.35、0.24、0.17、0.14。 在图6中,车辆平均速度随着道路上车辆密度的增大而减小,随着待停车辆比例系数f的增加,平均速度也随之下降得更多。随着车辆密度的增加,平均速度均趋向于0,出现了交通堵塞。 2.2 对时空演化斑图的分析讨论 根据数值模拟的数据得到的时空演化斑图如图7中的(a)、(b)、(c)、(d)所示,这些图为正在停车的车辆所在位置前后300个元胞的时空演化斑图。图中的横轴是车辆所在的位置,x=350~650(从左到右,停车车辆所在的位置为第530个元胞);纵轴是时间,y=30000 s~30200 s(从下到上)。黑色的地方表示元胞内有车,白色的地方表示元胞内无车。 图7 正在停车车辆所在位置前后300个元胞的时空演化斑图 由时空演化斑图(a)可看出,粒子分散较均匀,说明当车道上的车辆密度较小且停车车辆的比例系数也小时,道路畅通,出现畅行相。随着停车车辆在停车过程中对后车的阻碍时间T增加,粒子分散越来越不均匀,在停车车辆所在位置出现了比其他地方更黑的区域,如(b)、(c)、(d)所示。说明这里的车辆数目很多,出现了较严重的交通拥堵现象。比例系数f越大,拥堵的范围就越宽。这说明了待停车辆的比例系数是影响道路通行能力的一个重要因素。 本文针对带有路内停车带的单向单车道上车辆的行为过程建立车辆元胞自动机行为规则,并数值模拟周期边界条件下路内停车行为对后车的阻碍时间T和待停车辆占道路上总车辆数的比例系数f对道路交通的影响。研究结果表明,T和f对道路交通的影响都很大。停车车辆在停车过程所用的时间受驾驶员的驾驶技术、道路状况、停车位的位置、停车位的长度和宽度等多种因素的影响。《城市交通设计指南》指出,平行式路内停车带中,每个泊车位的长度为6 m,宽为2.5 m[8]。我们在对一些路内停车位的实测结果表明,无论是闹市区还是居民区,路内停车泊位的宽度都不够,最多是2 m,甚至有些只有1.8 m,长度最多是5.5 m。这样设计的主要原因是道路宽度不够。但是,这样就会造成停车所用时间的增加,在车流量较大的道路上容易出现阻塞现象,严重影响到道路的通行能力。因此,在道路比较窄的区域或车流较大的道路上,不应该设置路内停车带,或是减少路内停车带的泊位数目,以保证道路的畅通。 [1]刘小明,王力.考虑路内停车的元胞自动机交通流模型[J].吉林大学学报(工学版),2012,42(2):327-333. [2]郭四玲.元胞自动机交通流模型的相变特性研究和交通实测分析[D].南宁:广西大学,2006:15-22. [3]薛郁,董力耘,戴世强.一种改进的一维元胞自动机交通流模型及减速概率的影响[J].物理学报,2001,50(3):445-449. [4]耿克姣.城市路内停车的必然性和供求规划模型分析[J].交通标准化,2013(3):42-44. [5]胡兵,聂华波.关于路内停车问题的反思[J].交通标准化,2007(1):91-94. [6]梁玉娟.基于弯道影响的交通流特性研究[J].公路,2011(3):115-118. [7]刘章.交通流宏微观模型在城市道路交通中的应用及实测分析[D].南宁:广西大学,2008:10-19. [8]杨晓光.城市道路交通设计指南[M].北京:人民交通出版社,2003:85-87. [责任编辑 刘景平] Analysis of the effect of Curb Parking on Traffic Flow WEI Lan-xiang, LIANG Yu-juan, ZHONG You-kun (School of Physics and Mechanical & Electrical Engineering, Hechi University, Yizhou, Guangxi 546300, China) In view of the vehicle behavior on the single lane with curb parking strip, the behavior rules of cellular automata are established and there will be a numerical simulation for the effect on the road traffic exerted by the proportional coefficient f of the vehicle to be parked on the road under the periodic boundary condition and by the blocking time T caused by the vehicle behavior on the curb parking blocking the vehicles behind.The results of the study show that f and T have great effect on road traffic. curb parking; traffic flow; the single lane; cellular automata 韦兰香(1979-),女,广西东兰人,河池学院物理与机电工程学院讲师,主要研究方向:交通流、大学物理教学。 广西高校科学技术研究项目(2013ZD059);广西高校优秀人才资助计划项目(桂教人〔2011〕40号);河池学院重点科研课题(2012YBZ-N006);河池学院青年科研课题(2013B-N002)。 U491.7;O313 A 1672-9021(2015)05-0055-07 2015-06-112 数值模拟与分析
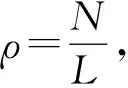
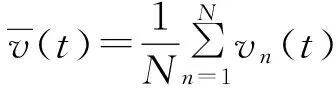
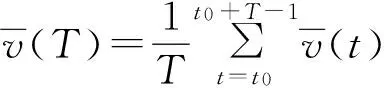
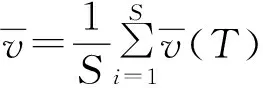

3 结论
