基于锯齿载波的最少开关次数调制波的PWM数学分析

陈国呈，蔡立清，周勤利，顾红兵，雷 电

(1．常州钜特工业科技有限公司，江苏常州200122;2．上海大学自动化学院，上海200072)

基于锯齿载波的最少开关次数调制波的PWM数学分析

陈国呈1，2，蔡立清1，周勤利1，顾红兵1，雷 电1，2

(1．常州钜特工业科技有限公司，江苏常州200122;2．上海大学自动化学院，上海200072)

文章分析了最少开关次数调制波的输出线电压波形，并根据三相逆变器实现软开关PWM动作需要，用双重傅里叶级数展开法解析了基于锯齿载波的最少开关次数调制波的PWM频谱特性。分析结果指出，该调制波虽是个不对称波，且含有直流分量，但其实质还是在正弦波基础上叠加了零序谐波分量和一个直流分量。这些零序谐波分量和直流分量在三相逆变器中相互抵消，其输出线电压还是正弦波。正是这种畸形波的调制作用，使得逆变器直流母线电压利用率得以提高，且正负序谐波幅值相差较小，能有效减小谐波损耗，提高波形质量，抑制谐波转矩脉动。通过与SAPWM比较后指出，最少开关次数调制波PWM只能使用单极性调制，其有效开关次数是后者的一半，电流波形质量不如后者。

最少开关次数调制波;锯齿载波;双重傅里叶级数;频谱;谐波

1 引言

在节能和环保意识日趋重视的当今时代，电力变换器的变换效率往往成为考核其性能的一个重要指标。半导体功率开关器件的开关损耗和导通损耗是影响电力变换器变换效率的重要因素，该损耗是器件出厂后所固有的，用户对此已无能为力。为了进一步提高变换器的变换效率，人们不得不从控制方法上另觅出路。众所周知的SPWM和SAPWM逆变器，其功率开关器件在调制波的全周期内都在进行PWM斩波和开关动作，从某种意义上说要减少其开关次数是不可能的，因此有学者提出了最少开关次数的调制波［1］。另一方面，为了减少噪声和电磁干扰，也为了进一步提高电力变换器的变换效率，20世纪90年代以来，电力变换器的软开关技术也受到了人们的高度重视［2-8］。在软开关电力变换中，传统的等腰三角载波无法得到应用，取而代之的是锯齿载波［9-14］。基于锯齿载波的PWM和基于等腰三角载波的PWM，其谐波特性有很大不同［15，16］，特别是其中基于锯齿载波的最少开关次数调制波的PWM数学分析还未见报道，本文就此做深入分析和推导，从中引出一些重要的结论。

2 最少开关次数调制波与调制模式

图1为三相逆变器主电路示意图，图2为文献［1］提出的最少开关次数调制波的生成方法。图2(a)为三相正弦波eU(t)、eV(t)、eW(t)，在此基础上做式(1)所示的波形叠加，即可得到图2(b)。

图1 三相逆变器主电路Fig．1 Main circuit of three-phase inverter

文献［17］以U相调制波eX(t)为例，进一步明确指出其表达式如式(2)所示，且在0～2π/3区间相位比eU(t)超前π/6，而在2π/3～4π/3区间比eU(t)滞后π/6。

图2 最少开关次数调制波的生成Fig．2 Generation of least switching modulation wave

可以看出在4π/3～2π区间，eX(t)不参与调制，逆变器的功率开关器件减少了1/3的开关损耗，故称之为最少开关次数调制波。由图2(b)和式(2)可以求出线电压UUV(ω1t)的数值如下:

0 ～2π/3区间:

2π/3～4π/3区间:

4π/3 ～2π区间:

显然，尽管调制波eX，Y，Z(t)为畸形波，但逆变器的输出线电压UUV(ω1t)在0～2π全区间内都保持着sinω1t的状态。从以上计算过程和结果还可以看出，调制信号eX(t)、eY(t)、eZ(t)里已包含了线电压和相电压的关系。下面的进一步分析结果还指出，本调制波也能提高输出电压15.47%。

3 数学分析

3.1 双重傅里叶级数展开式

众所周知，一个周期为2π的函数f(t)可以展开成如下傅里叶级数:

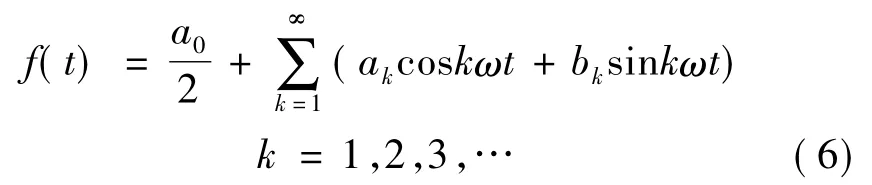
式中，a0/2为直流分量;为方便与后面的下标统一使用，式(6)中的下标用k表示，且

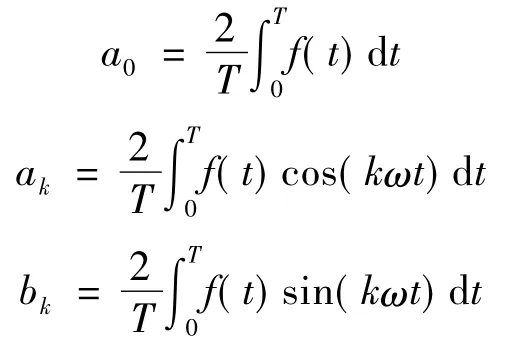
根据欧拉公式

将sinkωt和coskωt代入式(6)，得

式(7)被称为实函数f(t)的复数傅里叶级数。将a0、ak、bk的表达式代入式(8)中Kk的表达式，还可得到Kk的另一个表达式

现在来考察U相的电压UU，用双重傅里叶级数表示，有

式中，ω1为信号波角频率;ωs为锯齿载波角频率; Ed为直流母线电压。

同理可得V相的电压UV及U、V相间的线电压UUV的双重傅里叶级数表达式:

3.2 三相PWM变换器的数学分析

在软开关三相PWM变换器中，常常使用如图3所示的锯齿载波与调制波进行脉宽调制［9-14］，以实现软开关动作。因为锯齿波的高度必须定为1，为确保调制度与输出电压幅值保持线性关系，图2中的调制波幅值必须缩小倍，则由式(2)有

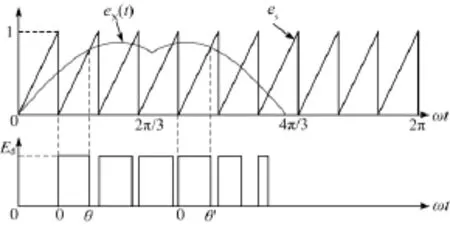
图3 最少开关次数调制波的锯齿波调制Fig．3 Least switching modulation with sawtooth carrier wave

本文旨在分析图3中调制波eX(t)与锯齿波es调制后的频谱及其输出特性。设M为调制深度，显然在0～θ和0～θ'区间，U相的输出电压为Ed，在此区间之外，输出电压为0。则由图3有:

(1)在调制波的 0～2π/3区间:θ= 2πMsinω1t。

(2)在调制波的 2π/3～4π/3区间:θ'= 2πMsin(ω1t－π/3)。

(3)在调制波的4π/3～2π区间:θ″=0。

由式(9)和式(12)有

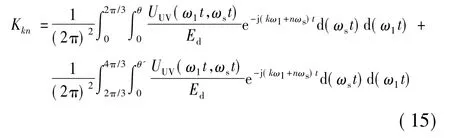
当0≤ωst＜θ及0≤ωst＜θ'时，UVU=Ed，UUV/Ed=1，在此区间之外，UUV/Ed=0，可以求出各谐波分量如下。图4展示了最少开关次数调制波三相输出电流的频谱，充分验证了两者的一致性。

图4 最少开关次数调制波的三相输出电流频谱Fig．4 Three-phase output current spectrum of least switching PWM

(1)直流成分(k=0，n=0)

又λ0=1－e－j0=0，所以K00λ0=0，即逆变器输出电压中不含直流分量，如图4所示。

(2)基波成分(k=1，n=0)

联系到式(8)，求实函数系数，得bn=M。代入式(6)，兼顾式(12)得式(18):

当k=3i(i=1，2，…)时

当k≠3i(i=1，2，…)时

所以Kk0λk≡0，即在基波频域除了基波成分ω1外，不存在其余谐波，如图4所示。

(4)各载波频域的谐波成分(k=0，n≥1)

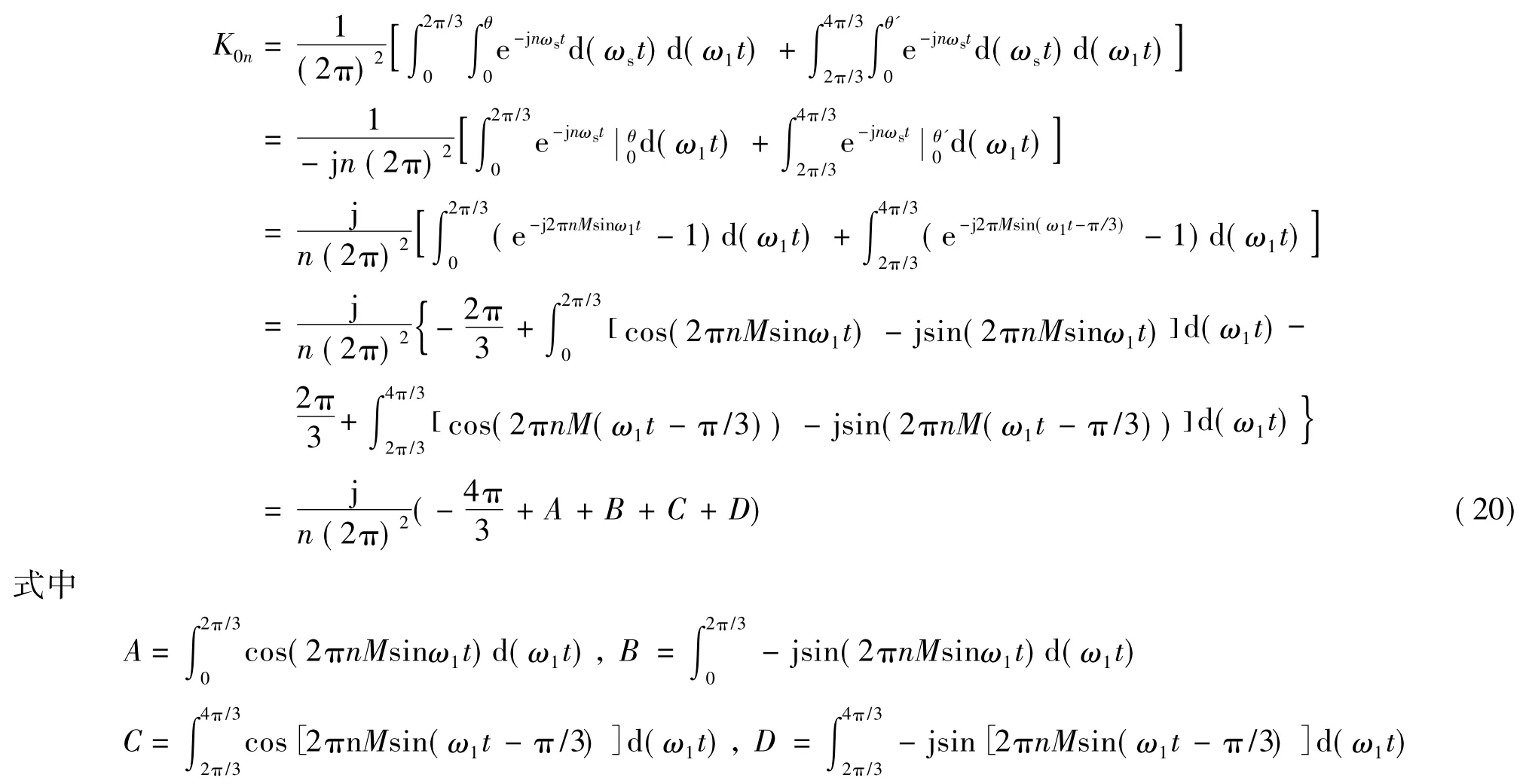
由贝塞尔函数

解得

则由式(20)有

因为λk=λ0=1－e－j0×2π/3=0，K0nλ0=K0n×0=0，所以在各载波频域不存在载波的整数倍成分nωs谐波，如图4中在频率1ωs、2ωs处都没有谐波，仿真时取载波频率为1.5kHz，相当于1ωs处。

(5)载波频率的边频带(k≠0，n≥1)

将式(23)和式(24)代入式(22)得

由于λk=1－e－jk2π/3，将其乘以式(25)有

将式(26)再整理，得

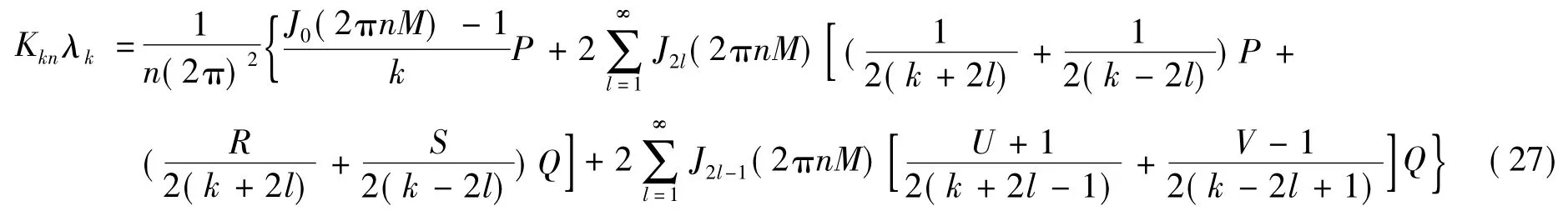
1)当k=3i(i=1，2，…)时，得P=0，Q=0，由式(27)有Kknλk=0，即在各载波频域不存在3的倍数次谐波，如图4所示，在3ω1、6ω1处都没有差频波。

联系到式(8)和式(9)可知，要使式(6)获得实系数，式(28)～式(30)的Kknλk只能取纯序数或实数，由于式(17)是纯虚数，而式(28)和式(30)是实数，所以这里只能取式(29)的虚部，即令

4 频谱归纳与分析

综合3.2节中的数学分析，对照式(6)，可以归纳最少开关次数调制波PWM的如下结论(参阅图4)。

(1)直流成分(k=0，n=0):K00λ0=0，bk= 0，频谱中不含直流分量。

(2)基波成分(k=1，n=0):三相逆变器输出线电压的基波分量UUV(ω1t)=MEdsinω1t，与正弦波PWM的输出MEdsinω1t相比，高出了15.47%。

(3)谐波成分(k＞1，n=0):Kk0λk=0，bk= 0，基波频域除了UUV(ω1t)=MEdsinω1t外，不含其余谐波。

(4)各载波频域的谐波成分(k=0，n≥1):λk=λ0=1－e－j0×2π/3=0，K0nλ0=0，即在各载波频域不存在载波的整数倍成分nωs谐波，如图4中在频率1ωs、2ωs处都没有谐波。

(5)载波频率的边频带(k≠0，n≥1):

当k=3i(i=1，2，…)时，Kknλk=0，即不存在3的倍数次谐波，如图4中的3ω1、6ω1等处都没有差频波;当k=3i+1(i=0，1，…)时，边频带谐波幅值如式(36)所示;当k=3i－1(i=1，2，…)时，边频带谐波幅值如式(37)所示。

联系式(12)、式(36)和式(37)可以看出，边频带谐波成分为ωs±ω1，ωs±2ω1，ωs±4ω1，ωs±5ω1，…和2ωs±ω1，2ωs±2ω1，2ωs±4ω1，2ωs±5ω1，…，这与图4的结果完全吻合。

从第3节的分析中可以看出，最少开关次数调制波是一个不对称的畸形波，对其直接进行傅里叶级数展开很困难，因此不得不使用双重傅里叶级数展开法分析。本方法计算量很大，也非常容易出错。这就是说，如果按传统方法把UUV(ω1t)看成是U相PWM调制结果与V相PWM调制结果相减而成，则其数学解析是非常麻烦的。但是，从式(3)～式(5)的推导来看，逆变器最终输出的线电压UUV(ω1t)还是个正弦波，如果将式(3)～式(5)看成在整个0～2π区间内是一个正弦波，则上述调制方法可权当看成是一个正弦波与载波(无论是等腰三角波还是锯齿波)的PWM，则其数学分析方法就可以沿用传统的傅里叶级数展开法［15-17］，分析方法容易得多，而两者的频谱分布位置基本一致。但需要注意的是，最少开关次数调制波本质上就是eU(t)、eV(t)、eW(t)加上零序分量和一个直流分量“－1”(即基波幅值1的负偏移量)，其零序分量为nω3(n=1，2，3，…)，若令ω3=3ω1，即ω3，2ω3，3ω3，4ω3，5ω3，…，是ω3的所有奇偶数倍次谐波，如图5所示。但SAPWM中叠加的零序分量为nω3(n =1，3，5，…)，只是3的奇数倍次谐波，且不叠加直流分量［15］。所以最少开关次数调制波的PWM谐波分量比SAPWM多，但在三相逆变器中这些零序分量和直流偏移量都抵消了。

图5 最少开关次数调制波的基波频域输出电流频谱Fig．5 Output current spectrum of least switching modulation in fundamental frequency domain

无论最少开关次数调制波PWM还是SAPWM，其三相输出电流的频谱分布规律与SPWM基本相同，但边频带中正负序谐波分量的幅值有所不同，前两者的正负序分量的幅值相差都较小，而后者则较大，如图4、图6和图7所示。图4和图6中，1ω1和2ω1、4ω1和5ω1、…相差都不大;图7是直接利用正弦波与锯齿波比较生成的三相输出电流频谱，其1ω1和2ω1的幅值相差很大。这是因为前两者实施PWM时是通过畸形波的PWM实现的，由于畸形波与正弦波波形的细微差异表现在对载波调制时生成的脉冲宽度分布规律有细微不同，从而造成正负序谐波幅值的差异。但正是该波形的这种畸变，使得逆变器输出线电压有效值提高了15.47%(所谓提高了直流母线电压的利用率)，同时降低了总谐波电流失真和谐波转矩脉动，称为优化的调制波。

图6 三相SAPWM逆变器输出电流频谱Fig．6 Output current spectrum of three-phase SAPWM inverter

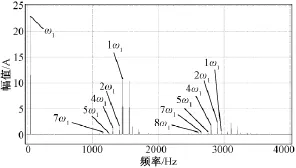
图7 三相SPWM逆变器输出电流频谱Fig．7 Output current spectrum of three-phase SPWM inverter

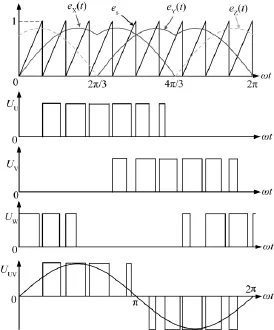
图8 最少开关次数调制波的输出线电压Fig．8 Output line voltages of least switching modulation

需要指出的是，图3所示的最少开关次数调制波从波形上看确实只有2/3调制周期参与调制，余下的1/3周期是闲置着的，这意味着使用该调制波可以减少1/3的开关损耗。但是众所周知，图3所示的调制方式是属于单极性调制，在三相逆变器输出线电压中，其有效开关次数是双极性调制的1/2，如图8所示。图8中，0～π/3期间，输出线电压UUV的前后沿次数就是UU的前后沿次数，因为此期间UV一直保持0电压。如果使用SPWM或SAPWM，则其可以使用双极性调制，在相同的载波频率下，SPWM和SAPWM输出线电压的有效开关次数是相电压时的2倍。有效开关次数提高之后，三相输出电流的脉动幅值相对减小了，有利于提高输出电流波形质量，使THD减小，同时减小功率开关器件的电应力、转矩脉动和电磁干扰等。这与多电平逆变器有相同之处，即功率开关器件的开关频率未必很高，但多电平逆变器整体的有效开关次数很高，从而提高逆变器输出的许多电特性。究其根本原因是，最少开关次数调制波的波形决定了其只能使用单极性调制，从而限制了其整体的有效开关次数。当然，为了提高逆变器输出电特性，也可以提高载波频率，但这就提高了逆变器功率开关器件整体的开关次数，反而抵消了本调制波可以减少1/3开关次数的所谓优点。本文讨论的载波是锯齿波，如果采用等腰三角载波，情况也是如此。

5 结论

本文分析了最少开关次数调制波的输出线电压波形，并采用双重傅里叶级数展开法分析了基于锯齿载波的最少开关次数调制波的PWM频谱特性。分析结果指出，最少开关次数调制波的本质是在正弦波基础上叠加了零序谐波分量和一个直流分量，这些零序谐波分量和直流分量在三相逆变器中相互抵消，其输出线电压还是正弦波。文章还指出最少开关次数调制波叠加的零序分量是基波角频率的所有3的倍数次谐波，而SAPWM叠加的只是3的奇数倍次谐波。两者正是利用该畸变波的调制作用，使得逆变器直流母线电压利用率得以提高，且正负序谐波幅值相差较小，能有效减小谐波损耗，提高波形质量，抑制谐波转矩脉动。对于这种不对称畸形波，采用双重傅里叶级数展开法分析其频谱特性相当麻烦，也容易出错。从本质上讲，该畸形波的三相输出线电压波形的PWM频谱分布规律与SPWM的分布规律相同，只是正负序谐波的幅值不一样，前者趋同，后者趋异，前者能获得更好的输出特性。但是，最少开关次数调制波属于一种单极性调制模式，而SPWM和SAPWM可使用双极性调制，其整体有效开关次数是前者的2倍，可获得更好的输出电特性。综合比较上述三种调制模式，SAPWM为最优。因此SAPWM已被普遍应用，但最少开关次数调制波没能获得推广应用。

［1］谷口勝則，入江寿一(Taniguchi Katsunori，Irie Hisaichi)．三相正弦波PWMパターンのための変調信号(Modulation signal for the three-phase sine wave PWM pattern)［J］．電気学会論文誌(Journal of Institute of Electrical Engineers of Japan)，1985，105(10):880-886．

［2］I Barbi，J C Bolacell，D C Martins，et al．Buck quasiresonant converter operating at constant frequency:analysis，design，and experimentation［J］．IEEE Transactions on Power Electronics．1990，5(3):276-283．

［3］Hua Guichao，Yang Eric X，Jiang Yimin，et al．Novel zero-current-transition PWM converters［J］．IEEE Transactions on Power Electronics，1994，9(6):601-606．

［4］Mao Hengchun，Lee Fred C Y，Zhou Xunwei，et al．Improved zero-current transition converters for high-power applications［J］．IEEE Transactions on Industry Applications，1997，33(5):1220-1232．

［5］Jinrong Qian，Fred C Lee，Tokushi Yamauchi．New continuous-input current charge pump power-factor-correction electronic ballast［J］．IEEE Transactions on Industry Applications，1999，35(2):433-441．

［6］Jia Wu，Fred C Lee，D Boroyevich，et al．A 100kW high-performance PWM rectifier with a ZCT soft-switching technique［J］．IEEE Transactions on Power Electronics，2003，18(6):1302-1308．

［7］Yong P Li，Fred C Lee，Dushan Boroyevich．IGBT device application aspects for 50 kW zero-current-transition inverters［J］．IEEE Transactions on Industry Applications，2004，40(4):1039-1048．

［8］Yong Li，Fred C Lee．A generalized zero-current-transition concept to simplify multilevel ZCT converters［J］．IEEE Transactions on Industry Applications，2006，42(5):1310-1320．

［9］陳国呈，谷口勝則，中村博人(Chen Guocheng，Taniguchi Katsunori，Nakamura Hiroto)．ソフトスイッチング三相インバータのPWM手法(PWM technique of soft switching three-phase inverter)［A］．日本電気学会全国応用大会講演論文集(NEC Society national application Conference Papers)［Ⅱ］［C］．長崎，日本(Nagasaki，Japan)，1999.17-20．

［10］Lee S R，Ko S H，Kwon S S，et al．An improved zerovoltage transition inverter for induction motor drive application［A］．Proceedings of the IEEE Region 10 Conference，TENCON 99［C］．1999.986-989．

［11］陈国呈，谷口勝則，中村博人(Chen Guocheng，Taniguchi Katsunori，Nakamura Hiroto)．软开关三相变频器的PWM方法(Soft-switching PWM method of threephase inverter)［J］．电工技术学报(Transactions of China Electrotechnical Society)，2000，15(6):23-27．

［12］陈国呈，谷口勝則，张晓东，等(Chen Guocheng，Taniguchi Katsunori，Zhang Xiaodong，et al．)．高功率因数三相软开关 PWM变流器(High power factor three-phase soft-switching PWM converter)［J］．电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2001，20(2):7-10．

［13］许春雨，孙承波，陈国呈，等(Xu Chunyu，Sun Chengbo，Chen Guocheng，et al．)．ZVT软开关三相PWM逆变器控制策略研究(Study of control scheme in ZVT soft-switching three-phase PWM inverter)［J］．电工技术学报(Transactions of China Electrotechnical Society)，2004，19(11):36-41．

［14］娄慧波，毛承雄，陆继明，等(Lou Huibo，Mao Chengxiong，Lu Jiming，et al．)．基于锯齿波的载波移相脉冲宽度调制技术(Carrier phase shifted pulse width modulation technique based on sawtooth wave)［J］．高电压技术(High Voltage Engineering)，2012，38(4): 993-998．

［15］陈国呈，蔡立清，周勤利，等(Chen Guocheng，Cai Liqing，Zhou Qinli，et al．)．基于等腰三角载波的鞍形波PWM的数学分析(Mathematical analysis on saddle waveform PWM based on isosceles triangle carrier wave)［J］．电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2015，34(9):2-16，28．

［16］陈国呈，蔡立清，周勤利，等(Chen Guocheng，Cai Liqing，Zhou Qinli，et al．)．基于锯齿载波的SPWM及SAPWM的数学分析(Mathematical analysis on SPWM and SAPWM based on sawtooth carrier wave)［J］．电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2015，34(10):1-9，16．

［17］陈国呈(Chen Guocheng)．PWM逆变技术及应用(PWM inverter technology and applications)［M］．北京:中国电力工业出版社(Beijing:China Electric Power Industry Press)，2007．

Mathematical analysis on least switching PWM based on sawtooth carrier wave

CHEN Guo-cheng1，2，CAI Li-qing1，ZHOU Qin-li1，GU Hong-bing1，LEI Dian1，2
(1．Giant Industrial Technology Co．Ltd．，Changzhou 200122，China; 2．Department of Automation，Shanghai University，Shanghai 200072，China)

This paper analyzes the output line voltage waveform of least switching modulation，and in some cases，soft switching three-phase PWM inverters are required，using double Fourier series expansion method to resolve the PWM spectrum characteristics of the least switching modulation based on sawtooth wave carrier．The results indicate that although it is an asymmetric modulation wave，and contains a DC component，but its essence is superimposing zero sequence harmonic components and a DC component on a sine wave．These zero-sequence harmonics and DC components cancel each other out in a three-phase inverter，and the output line voltage is still a sine wave．Owing to the distorted modulation wave，the DC bus voltage utilization of inverter can be improved，and the difference of harmonic amplitudes between the positive and negative sequence is smaller，moreover，it can effectively reduce harmonic losses，improve waveform quality，and suppress harmonics torque ripples．After comparing the minimum switching frequency modulation with SAPWM，it may be noted that the minimum switching frequency modulation can only use unipolar modulation，the effective switching frequency is only half of the latter，so the current waveform quality is not as good as latter．

least switching modulation wave;sawtooth carrier wave;double Fourier series;spectrum;harmonic

TM464

:A

:1003-3076(2015)11-0001-10

2015-08-01

陈国呈(1944-)，男，福建籍，教授，博士生导师，主要研究方向为电机驱动及新能源发电;蔡立清(1970-)，男，安徽籍，工程师，主要研究方向为新能源发电逆变器、通信系统。