抽水蓄能电站水轮机模型参考自适应控制
2015-06-01晋萃萃杨春宇
晋萃萃,刘 禾,杨春宇
(1.华北电力大学 控制与计算机工程学院,北京102206; 2.国网吉林省电力有限公司 延边供电公司,吉林 延吉133000)
抽水蓄能电站水轮机模型参考自适应控制
晋萃萃1,刘 禾1,杨春宇2
(1.华北电力大学 控制与计算机工程学院,北京102206; 2.国网吉林省电力有限公司 延边供电公司,吉林 延吉133000)
将定常PID控制应用于对抽水蓄能电站水轮机的控制,针对水轮机调节系统时变特性的问题,研究了模型参考自适应控制方法,建立了水轮机调节系统线性化数学模型,并用模型参考自适应控制策略对抽水蓄能电站水轮机进行控制,同时结合李雅普诺夫稳定性理论和波波夫的超稳定性理论推导出控制器参数变化规则。进行了模型参考自适应控制器与PID控制器对机组控制的仿真研究,结果表明:自适应控制比PID控制响应速度快、超调量小、调节时间短、稳定性好,能够改善水轮机调节系统的动态特性与控制性能。
抽水蓄能电站;水轮机;模型;自适应控制
0 引言
抽水蓄能电站作为电网调频调峰的主要手段日显重要[1,2]。由于抽水蓄能水库水位变化范围较一般水库变化大,因此抽水蓄能的水轮机调节系统的时变、非线性特性就更加明显[3,4],使用定参控制策略难以保证系统具有良好的特性,甚至可能在某些工况下还会出现不稳定现象。为此,本文引入模型参考自适应控制策略对抽水蓄能电站水轮机进行控制研究。
1 系统模型
1.1 系统结构
并网后水轮机调节系统[5,6]结构如图1。

图1 水轮机调节系统结构
1.2 机械液压系统
机械液压系统由电气-位移转换部分和液压放大部分组成,数学表达式[7,8]为:
(1)
式中:Δy为水轮机调速器导叶接力器行程相对量增量,Δyout为控制器输出相对量增量,Ty是接力器响应时间常数。
1.3 引水系统和水轮机
水轮机转矩mt和流量qt是导叶开度y、水头h和机组转速n的函数[9]。如果用相对值表示,则有:
mt=mt(y,x,h)
(2)
mt=mt(y,x,h)
(3)
在研究小波动的情况下,可分别将式(2)和(3)用泰勒级数展开,略去二阶以上高次项,可得:
(4)
(5)

引水系统的特性可表示为:
(6)
式中:Tw为引水系统水流惯性时间常数。
因此在稳定工况点附近,引水系统和水轮机的传递函数为:
(7)
1.4 发电机
机组运行时发电机数学模型表示成功率与转
矩的关系式为:
(8)
鉴于机组并网后,机组频率会受到电网影响,发电机数学模型表示成频率与转矩的关系式为:
(9)
式中:Δmt为水轮机转矩相对增量;P为机组功率;f为机组频率;Ta、Tb是机组惯性时间常数;k为机组出力与频率的线性关系。
1.5 广义被控对象模型
在稳定工作点附近,水轮机广义被控对象数学模型的传递函数[5]为:
理想抽水蓄能水轮机的传递系数为:ey=1,eh=1.5q,eqy=1,eqh=0.5q,eqx=0,系统传递函数可简写成为:

(10)
2 模型参考自适应控制
本文以某抽水蓄能电站的300MW机组水轮机为例,水轮机额定转速为500r/min,机组最大瞬态飞逸转速为718r/min,对于理想模型,相对流量q为1,水轮机参考模型的传递函数为:
(11)
水轮机水头发生变化时,被控对象的传递函数为:
(12)
式中:h=-Twqs。参考模型的状态方程和观测方程表示为:
xm(t)=Am(t)x+Bm(t)r(t)
ym(t)=cm(t)xm(t)
式中:
被控对象的状态方程和观测方程表示为:
xp(t)=Ap(t)xp(t)+Bp(t)u(t)
yp(t)=cp(t)xp(t)
式中:
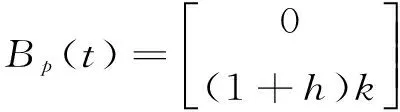
于是由参考模型和被控对象组成的控制系统如图2。由图2知,g为对可调系统前馈增益,可进行整定;r(t)为参考输入;F为可调系统的反馈增益向量[10]。
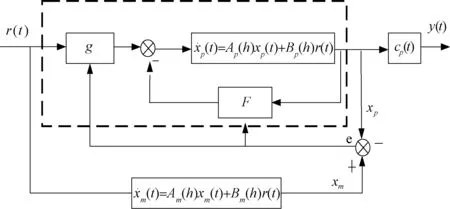
图2 模型参考自适应控制系统
由图2可得:
u(t)=r(t)-Fxp(t)
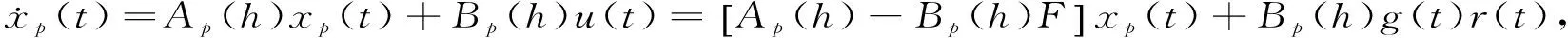
(13)
才有可能使可调系统对参考输入r(t)的动态响应与参考模型一致。
由于水位变化缓慢,因此参数Ap(h)和Bp(h)的变化比可调系统和参考模型动态响应过渡过程要慢,也比g(t)和f(t)自适应调整过程慢,是慢变函数,那么在调整过程中可以导出:
因状态偏差
e(t)=xm(t)-xp(t)
令
Φ(t)=Am-Ap(h)-Bp(h)f(t)
(14)
φ(t)=Bm-Bp(h)g(t)
(15)
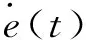
(16)
令Σ为包含变量e,Φ,φ的一个三维偏差空间,设εT=(e,Φ,φ)为空间Σ的向量。选择李雅普诺夫函数为
(17)

如果选择
(18)
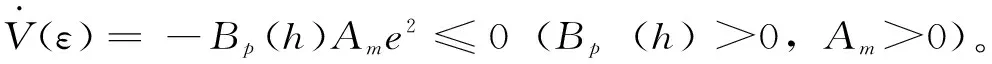
因此,可调系统反馈增益f(t)和前馈增益g(t)的自适应调整率满足:
(19)
利用这个规律调整可调系统,最后可达到,当t→∞时,e=0,Φ(t)=0,φ(t)=0,即
Ap(h)+Bp(h)f(t)=Am
Bp(h)g(t)=Bm
从而可知可调系统输出的动态响应和参考模型输出一致。
3 控制效果比较
水轮机调节系统水头为500m与480m时,分别对其采用PID控制与模型参考自适应控制,其中自适应控制中的控制器按式(18)的规律随水头变化自调整参数,研究分析不同水头下PID控制与模型参考自适应控制方式控制效果。
水头500m时,被控对象参数:eh=1.5,eqh=0.5,Tw=1.0,Ta=8.0,ts=0.1,En=1.0。水轮机工作在100 MW时受到100 MW的阶跃信号作用,分别使用PID和自适应两种控制方式,PID控制时,控制参数:kp=0.5,ki=1.0,kd=2.0,bp=0.05;自适应控制时,控制参数:k1=0.8,k2=0.8,k3=2.1,bp=0.05。机组功率特性响应曲线如图3所示。
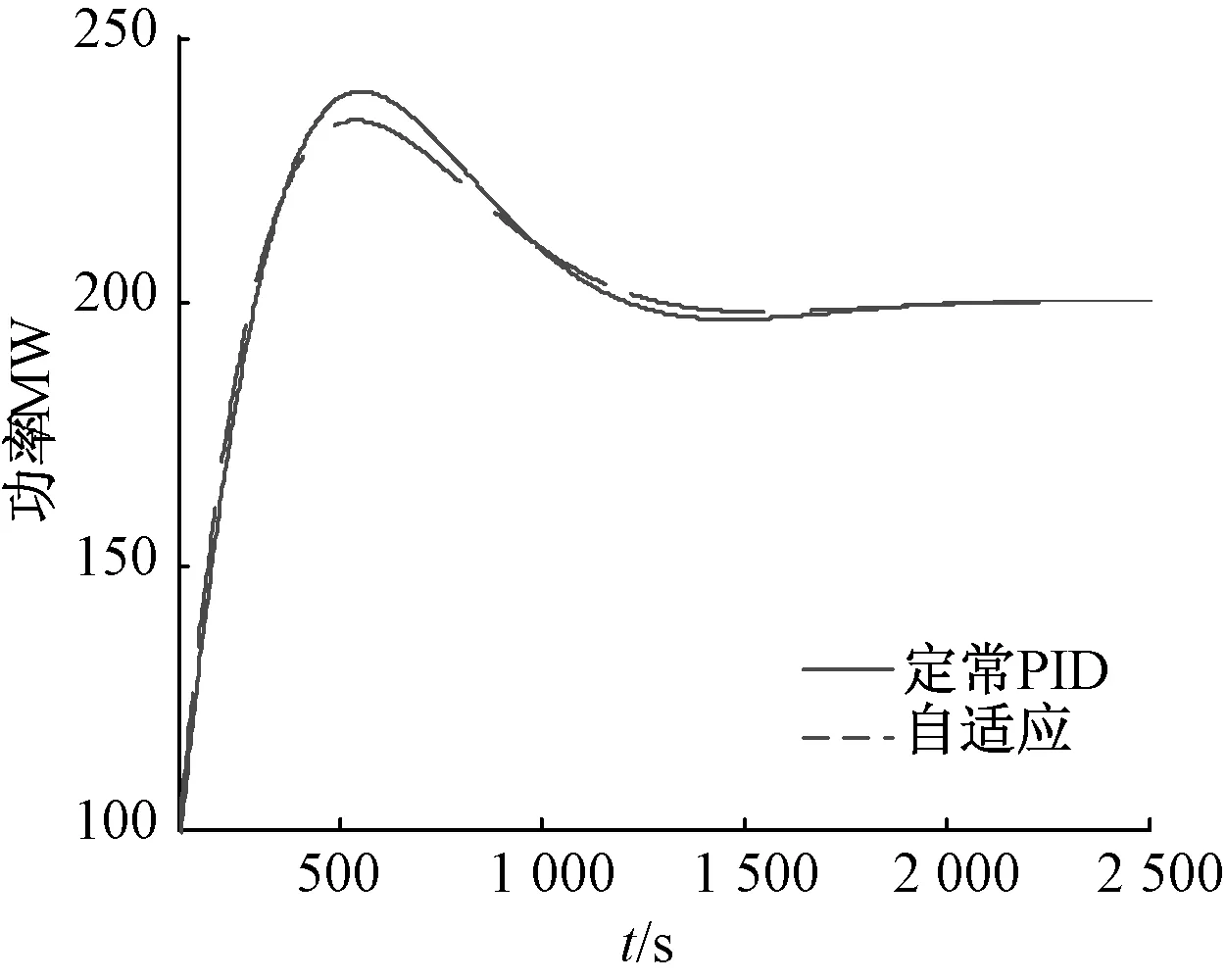
图3 水头500m时水轮机阶跃响应曲线
水头下降到480 m时,被控对象参数:eh=1.72,eqh=0.58,Tw=1.0,Ta=8.0,ts=0.1,En=1.0。PID控制参数不变,自适应控制参数为:k1=1.12,k2=0.96,k3=2.12,bp=0.05。机组功率仿真曲线如图4所示。
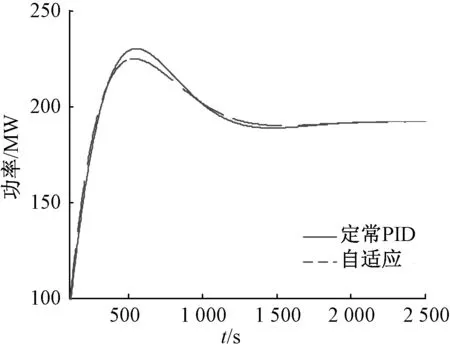
图4 水头480 m时水轮机阶跃响应曲线
由图3、4可看出水轮机运行过程中,自适应控制方式取得了比PID控制响应速度快、超调量小、调节时间短、稳定性好等良好的控制效果,从而提高了系统的动态性能。
在500 m水头时,水轮机组受到10%额定功率的外界扰动,对被控对象采用PID控制和自适应两种控制方式,控制效果如图5所示。
水头下降到480 m时,水轮机组受到10%额定功率的外界扰动,两种控制方式如图6所示。
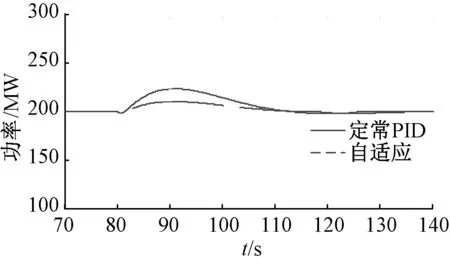
图5 水头为500m水轮机组负荷扰动功率特性曲线

图6 水头为480m水轮机组负荷扰动功率特性曲线
由图5、6可知,水轮机在稳定状态受到外界扰动,定常PID控制下机组功率特性变化幅度大,达到稳定所需时间长;而自适应控制可随实际输出和理想输出的偏差改变控制策略,消除不稳定因素,受到外界扰动后能很快恢复稳定运行。
4 结论
为抽水蓄能电站水轮机建立了数学模型,根据对象时变特性,使用李雅普诺夫稳定性理论和波波夫的超稳定性理论可推导出模型参考自适应控制器,实现水轮机自适应控制。比较分析两种控制效果可知模型参考自适应控制较PID控制超调量小、调节时间短、稳定性好、控制性能良好,能够优化PID控制效果。
[1]徐飞,陈磊,金和平,等.抽水蓄能电站与风电的联合优化运行建模及应用分析[J].电力系统自动化,2013,37(1):149-154.
[2]程雄,申建建,程春田,等.大电网平台下抽水蓄能电站群短期多电网启发式调峰方法[J].电力系统自动化,2014,38(9):53-60.
[3]李意扬,吴定会.基于风能转化系统的模糊PID自适应控制[J].江南大学学报(自然科学版),2013,12(1):17-22.
[4]张建辉,刘友宽,李晓娇,等.PID参数自适应控制下的汽轮机功率抗扰研究[J].电力科学与工程,2013,29(8):33-38.
[5]魏守平.水轮机调节系统仿真[M].武汉:华中科技大学出版社,2011.
[6]魏守平.水轮机调节系统一次调频及孤立电网运行特性分析及仿真[J].水电自动化与大坝监测,2009,33(6):27-33.
[7]刘昌玉,李崇威,洪旭钢,等.基于改进粒子群算法的水轮机调速系统建模[J].水电能源科学,2011,29(11):124-127.
[8]谭波,张荣,王江淮.基于物理机理建模的抽水蓄能机组仿真研究[J].电力科学与工程,2011,27(6):57-62.
[9]刘晓丽,郑源,高亚楠.抽水蓄能电站可逆机组导叶关闭规律探析[J].水电能源科学,2011,29(6):151-153.
[10]郑黎明,许移庆.变速风力发电机模型参考自适应控制[J].华北电力大学学报,2005,32(2):57-61.
Hydro-turbine Model Reference Adaptive Control in Pumped Storage Power Station
Jin Cuicui1, Liu He1, Yang Chunyu2
(1.School of Control and Computer Engineering, North China Electric Power University, Beijing 102206, China; 2. Yanbian Power Supply Company, Jilin Electric Power Company, State Grid Corporation of China, Yanji 133000, China)
Aiming at the time-varying characteristics of hydro-turbine, hydro-turbine model reference adaptive control, which is employed in hydro-turbine regulation system, is researched in this paper. Then the control of hydro-turbine of pumped storage power station based on PID control is put forward. And the mathematical model of hydro-turbine regulation system is established. Combined with Lyapunov stability theory and Popov super stability theory, the change rules of controller parameters have been deduced. The simulation results show that adaptive control performs better in adaptability, stability, overshoot and regulation time than PID control.
pumped storage power station; hydro-turbine; model; adaptive control
2015-06-29。
晋萃萃(1991-),女,硕士研究生,研究方向为水利水电等方面,E-mail:jincuicui2012@126.com。
TK734
A
10.3969/j.issn.1672-0792.2015.09.009
