关于非自反空间类映射的拓扑度
2015-06-01吴柳婵陈晓玲
吴柳婵,陈晓玲
(广东工业大学 应用数学学院, 广东 广州 510520)
吴柳婵,陈晓玲
(广东工业大学 应用数学学院, 广东 广州 510520)
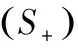
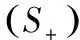
拓扑度理论是研究非线性算子定性理论的有力工具,从它可推出许多著名的不动点理论.研究非线性方程解的问题在理论上和应用上都十分重要,但常用的解析工具(如压缩映射)处理非唯一(例如出现分歧现象)的解却无能为力.度理论的建立,为研究非线性方程多解问题提供了有力工具,它能导出非线性方程解的许多结果,还可推出许多著名的不动点定理.因此,拓扑度理论直接或间接地在物理、力学、微分方程等学科里获得了广泛的应用.
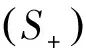
1 预备知识
为了讨论问题方便起见,本文出现的空间E均为实非自反Banach空间(没有特别说明的情况下),E*为E的共轭空间,E**为E*的共轭空间,Ω⊂E**为非空有界开子集.
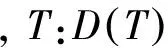
φ,T:ΩF→E*按范数拓扑连续,则称T为有限维连续.
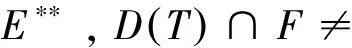

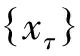
弱*收敛于f0=Tx0.
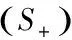
(1) 存在Ttx:[0,1]×D→E*为有限维连续;
(2) 任取
弱*收敛于
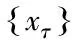
弱*收敛于f0=Tt0x0.
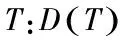
弱*收敛于
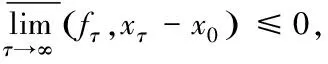
则称T为广义伪单调映射.
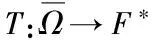
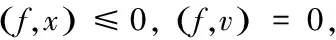
对任意v∈F0都成立,其中d(·,·,·)为有限维空间连续映射的拓扑度.
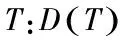
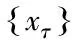
(1)
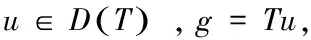


(2)

证明 设xτ∈E**,fτ=Txτ,gτ=φxτ,xτ弱*收敛于x0,满足

引理3[20]设E为实Banach空间,若E*可分,则E可分.
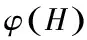
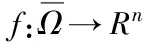
2 主要结论
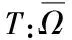
则存在有限维F0⊂E**,使得任意有限维空间F⊃F0,均有θ*∉TFx,对任意x∈∂ΩF都成立.
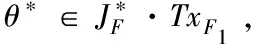
令WF={任取x∈∂Ω,存在f=Tx,使得
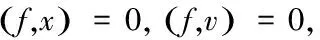
对任意v∈F都成立}为有界集且WF≠φ
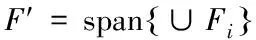
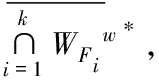
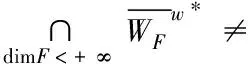
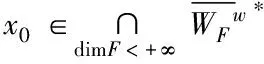
对任意v∈F,取F0,dimF0<+∞,使得
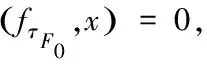


矛盾.故存在有限维F0⊂E**,使得任意有限维空间F⊃F0,均有θ*∉TFx,对任意x∈∂ΩF都成立.
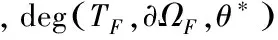
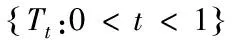
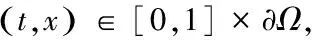
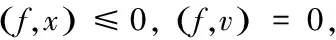
对任意v∈F都成立}.则WF≠φ
是WF在[0,1]×E**的闭包.
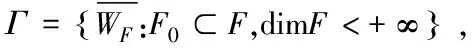
使得tτ→t0,xτ弱*收敛于
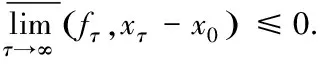
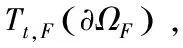
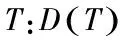
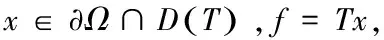
由以上的命题,可定义
⊃F0,dimF<+∞,dimF0<+∞.
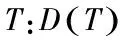
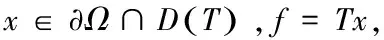
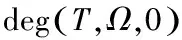
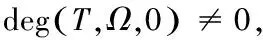
(2) 若Ω1,Ω2均是Ω的开子集,Ω=Ω1∪Ω2,Ω1∩Ω2=φ,则

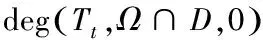
证明 (1)和(2)的证明同有限维空间的性质[22];
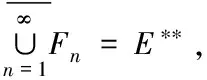
则

矛盾.
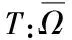
证明 假设F为Hilbert空间,则F*=F.对于有限维空间
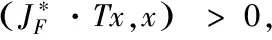
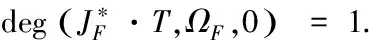
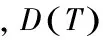
⊆
φ.
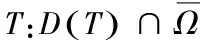
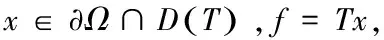
则存在N>0,使得0∉
⊆
对任意n>N,其中

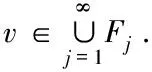
弱*收敛于
矛盾.
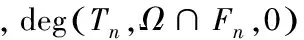
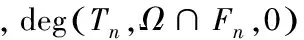
任意v∈Fnk都成立.任取x∈Fnk,k=1,2,…,假设xτk弱*收敛于x0,同命题6的证明,有
弱*收敛于
对任意v∈Fnk矛盾.
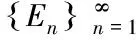
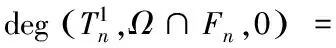

证明 令
由命题7知,存在N1>0,N2>0,当n>N1,N2时,有
(3)
(4)
结合式(3)和(4),故
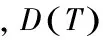
⊆
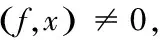
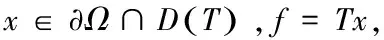
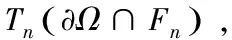
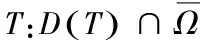
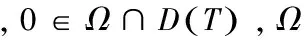
⊂E**非空有界开子集⊂E**的稠密子空间为的有限维空间序列⊆
满足Ω∩Fn≠φ,若
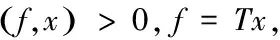
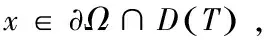
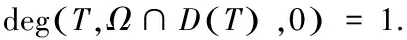
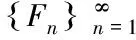
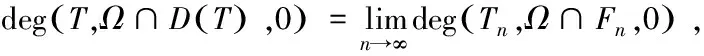
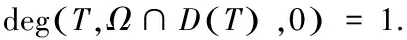
[1]BrowderFE.Fixedpointtheoryandnonlinearproblems[J].BullAmerMathSoc,1983,1:1-39.
[2]LerayJ,SchauderJ.TopologieetequationsFonctionnelles[J].AnnSciEcoleNormSup,1934,51:45-78.
[3]BrowderFE.Degreeofmappingsfornonlinearmappingsofmonotonetype[J].ProcNatAcadSci,1983,80:1771-1773.
[4]ZhangSS,ChenYQ.Degreetheoryformultivalued(S)typemappingsandfixedpointtheorems[J].ApplMathMech,1990,11(5):441-454.
[5]ChenYQ,O’ReganD,WangFL,etal.Anoteonthedegreeformaximalmonotonemappingsinfinitedimensionalspaces[J].ApplMathLetters,2009,22(11):1766-1769.
[6]ChenYQ,WangFL,O’ReganD.Degreetheoryformappingsofclass(S+)innon-reflexiveBanachspaces[J].ApplMathComputer,2008,202(1):229-232.
[7]ChenYQ,O’ReganD.CoincidencedegreetheoryformappingsofclassL-(S+) mapping[J].Appl Anal,2006,85:963-970.
[8] O’Regan D,Cho Y J,Chen Y Q.Topological degree theory and applications[J].Boca Raton:Chapman and Hall/CRC Press,2006,:127-168.
[9] Chen Y Q,Cho Y J.Topological degree theory for multi-valued mappings of class(S+) mappings[J].Arch Math,2005,84(4):325-333.
[10] Chang S S,Lee B S,Chen Y Q.Variational inequalities for monotone operators in non-reflexive Banach Spaces[J].Appl Math,1995,8(6):29-34.
[11] Chen Y Q,O’Regan D.On the homotopy property of topological degree for maximal monotone mappings[J].Appl Math Comput,2009,208(2):373-377.
[12] Petryshyn W V,Fitzpatrick P M.A degree theory,fixed point theorems,and mapping theorems for multivalued noncompact mappings[J].Amer Math Soc,(1974),194: 1-25.
[13] Adhikari D R,Kartsatos A G.A new topological degree theory for perturba-tions of the sum of two maximal monotone operators[J].Nonlinear Anal,2011,74(14):4622-4641.
[14] Aizicovici S, Chen Y Q.Note on the topological degree of the sub-differential of a lower semi-continuous convex function[J].Proc Amer Math Soc,1998,126:2905-2908.
[15] Berkovits J, Mustonen V.On the degree for mappings of monotone type[J].Nonlinear Anal, 1986,12:1373-1383.
[16] Browder F E.Degree of mappings for nonlinear mappings of monotone type:densely defined mappings[J].Proc Nat Acad Sci,1983,80:2405-2407.
[17] Browder F E,Petryshyn W V.Approximation methods and the generalized topological degree for nonlinear mappings in Banach spaces[J].Funct Anal,1969,3:217-274.
[18] Troyanski S.On locally uniformly convex and differentiable norms in certain non-separable Banach spaces[J].Studia Math,1971,37:173-180.
[19] Chen Y Q,Wang F L,O’Regan D.Degree theory for monotone type mappings in non-reflexive Banach spaces[J].Appl Math Lett,2009,22(2):276-279.
[20] 张恭庆,林源渠.泛函分析讲义:上册[M].北京:北京大学出版社,1987:126-145.
[21] 郭大钧.非线性泛函分析[M].2版.济南山东科学技术出版社,2001:87-135.
[22] Wang F L,Chen Y Q,O’Regan D.Degree theory for monotone type mappings in non-reflexive Banach spaces[J].Appl Math Lett,2009,22(2):276-279.
Wu Liu-chan,Chen Xiao-ling
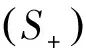
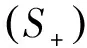
2013- 06- 07
吴柳婵(1989-),女,硕士研究生,主要研究方向为非线性泛函分析.
10.3969/j.issn.1007- 7162.2015.01.028
O177.91
A
1007-7162(2015)01- 0138- 05
(School of Applied Mathematics, Guangdong University of Technology, Guangzhou 510520,China)
