基于交互多模型的测量噪声累积误差修正方法研究
2015-06-01刘国霞闫安萍
刘国霞,闫安萍
(南京电子技术研究所,江苏南京210039)
基于交互多模型的测量噪声累积误差修正方法研究
刘国霞,闫安萍
(南京电子技术研究所,江苏南京210039)
针对传感器的测量噪声水平会随时间变化,很难用单个的测量噪声水平模型进行描述;提出利用多个描述目标不同测量噪声水平模型次优的交互多模型方法。与单个模型的跟踪方法相比,多模型能够自适应修改不同模型的比例权重,从而选择局部最优的组合去逼近真实值,整个过程不需要设计复杂的逻辑跳变,具有较强的实用性。最后,通过仿真进一步验证了该方法的有效性和可行性。
交互多模型;测量噪声;累积误差修正;自适应
0 引言
在现代电子战中,传感器的工作环境极其恶劣。传感器的测量精度不仅仅由自身的物理条件所限制,而且还受工作环境好坏的影响。因测量环境的复杂性及不确定性,传感器特别是被动传感器的测量数据一般随时间有一定程度的累积,现有的估计理论一般都认为测量噪声水平是已知的,这与实际情况不相符,势必导致定位精度的下降。因此有必要深入研究测量噪声累积误差[1⁃2]修正的问题。
1 交互多模型跟踪算法
正如前面所提,传感器实际的测量噪声水平和变化趋势不能准确获得,很难用单个的测量噪声水平模型进行描述。测量噪声水平随时间的变化会引起跟踪模型与实际模型之间的失配,不仅对定位精度产生较大的影响,甚至会导致跟踪发散。因此基于单个模型的算法难以获得令人满意的结果;次优的交互多模型[3⁃6](IMM)算法使用多个描述目标,不同测量噪声水平的模型进行交互跟踪目标,由于其结构简单、效费比高而倍受青睐。
正因为交互式多模型效费比高,并且模型切换不需要复杂的逻辑跳变设计,因此重点探讨交互式多模型对累积测量误差修正的方法。
本文将探讨被动传感器在不同测量噪声水平交互作用下的跟踪效果,同等条件下分别比较单个测量噪声水平的跟踪精度,给出相应的分析结论。下面简要介绍交互多模型滤波算法流程:
(1)跟踪模型建立
IMM算法中第j个模型的状态方程及量测方程为:

式中:Fj(⋅)为模型j的非线性方程;Hj(⋅)为模型j的量测函数;Vj为不相关的零均值高斯白噪声,其方差为Rj。因为各个模型微分方程都为非线性方程,都采用非线性的滤波方法进行滤波,本项目采用SRF[7⁃9](Shift Rayleigh Filter)作为基础滤波器。
(2)输入交互
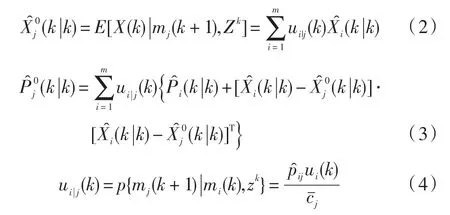
(3)滤波计算
(4)模型概率更新

(5)输出交互
将以模型为条件的估计和协方差组合,得到系统最终的估计结果。
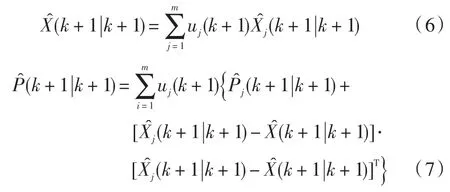
通过上述多模型的办法对空中目标进行跟踪,与单个模型的跟踪方法相比,多模型能够自适应修改不同模型的比例权重,从而选择局部最优的组合去逼近真实值,整个过程不需要设计复杂的逻辑跳变,具有较强的实用性。
2 仿真结果与分析
2.1 仿真场景设置
假设被动传感器测量噪声随时间而变,测量噪声前300 s为1°,301~600 s为5°,601~900 s为8°。交互多模型集测量噪声为[0.5°,1°,2°,4°,8°]。传感器与目标的相对场景图如图1所示,传感器的测量角度如图2所示。
用5个单模型与交互多模型的跟踪误差比较图,如图3所示。图4,图5是交互多模型的模型概率转换图。
图1 仿真场景图
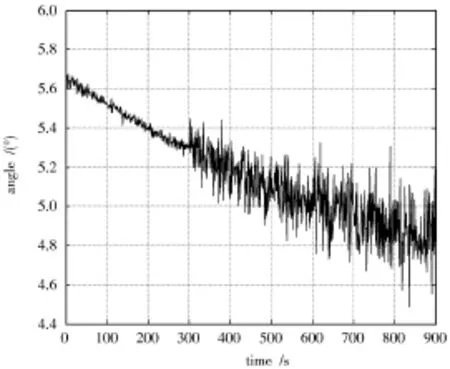
图2 测量角度
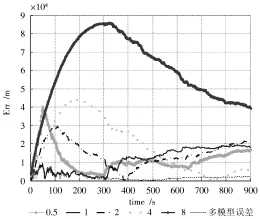
图3 跟踪误差比较图
2.2 仿真结果与分析
从图2可知,传感器的测量误差随着时间在不断累加。这正是累积测量误差的体现,图3是交互式多模型和各个单模型跟踪误差比较图,从图中可得交互式多模型的跟踪效果比任何一个单模型都要好,更为重要的是它并不随着累积测量误差的增加而精度变差,它的跟踪精度、稳定性和鲁棒性都比单模型要好得多。
图4,图5体现了交互式多模型的工作过程,它会自适应调整最相似的模型以最大的概率去跟踪实际目标,例如在前面300 s中,1°模型占的概率超过90%,而300~600 s时4°模型占主要成分,600~900 s时8°模型也起重要作用,这个过程与实际的噪声大小是相符的,体现了交互式多模型的有效性。

图4 IMM模型概率转换图(一)
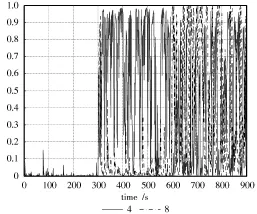
图5 IMM模型概率转换图(二)
3 结论
仿真结果验证了采用交互式多模型对于累积测量噪声具有较好的修正效果,与单模型跟踪效果比较,无论是在跟踪精度、跟踪的稳定性以及鲁棒性都具有较大程度的提高。
[1]周宏仁,敬忠良,王培德.机动目标跟踪[M].北京:国防工业出版社,1991.
[2]何友,修建娟,张晶炜,等.雷达数据处理及应用[M].北京:电子工业出版社,2006.
[3]BLOM H A P,BAR⁃SHALOM Y.The interacting multiple model algorithm for systems with Markovian switching coeffi⁃cients[J].IEEE Transactions on Automatic Contro1,1988,33(8):780⁃783.
[4]王志敏,肖卫初.机动目标跟踪IMM算法的性能分析[J].湖南城市学院学报,2003,24(6):109⁃111.
[5]LI R X,JILKOV V P.A survey of maneuvering target tracking:dynamic models[C]//Proceedings of SPIE Conference on Sig⁃nal and Data Processing of Small Targets.Orlando:IEEE,2000:4048⁃4052.
[6]徐毓,金以慧.相关噪声下的机动目标跟踪SMFEKF⁃IMM算法[J].清华大学学报:自然科学版,2003,43(7):865⁃868.
[7]CLARK J M C,VINTER R B,YAQOOB M M.The shifted Rayleigh filter for bearings only tracking[C]//Proceedings of the 8th International Conference on Information Fusion.[S.l.]:IEEE,2005,1:93⁃100.
[8]CLARK J M C,ROBBIATI S A,VINTER R B.The shifted Rayleigh mixture filter for bearings⁃only tracking of maneuve⁃ringtargets[J].IEEETransactionsonSignalProcessing,2007,55(7):3218⁃3226.
[9]CLARK M,MASKELL S,VINTER R,et a1.A comparison of the particle and shifted Rayleigh filters in their application to a multisensor bearings⁃only problem[C]//Proceedings of 2005 IEEE Aerospace Conference.Big Sky:IEEE,2005:2142⁃2147.
Correction method based on interaction multi⁃model for measurement noise cumulative error
LIU Guoxia,YAN Anping
(Nanjing Research Institute of Electronics Technology,Nanjing 210039,China)
Since sensor measurement noise level changes with time,it is difficult to describe with a single measurement noise level model.The suboptimal interaction multi⁃model method of different measurement noise level models for multiple de⁃scription objects is proposed in this paper.Compared with the single model tracking method,multi⁃model method can modify the proportion weight of different models adaptively,so that local optimal combination is selected to approximate the true value.It is unnecessary to design complex logic jumping in the whole process because it has strong practicability.The validity and feasibili⁃ty of the proposed method was verified further by simulation.
interaction multi⁃model;measurement noise;cumulative error correction;self⁃adaption
TN103⁃34
A
1004⁃373X(2015)13⁃0024⁃03
刘国霞(1982—),女,宁夏同心人,硕士,工程师。主要从事雷达数据处理。
闫安萍(1973—),女。主要从事机载雷达数字系统集成。
2015⁃01⁃23
