超声波振动切削TC4钛合金的残余应力数值分析

中航工业沈阳黎明航空发动机(集团)有限责任公司 杨万辉 陈 雷 杨金发 杨惠欣

TC4钛合金因质量轻、强度高、耐热性好、抗腐蚀性强而被广泛应用于航空航天工业，但钛合金切削过程具有冷硬现象严重、切削温度过高、刀具易粘附磨损等特点。超声波振动切削是一种具有分离和变速特性的脉冲式切削技术，可有效降低切削力和切削热，提高刀具使用寿命，改善工件表面加工质量。因此，超声波振动切削成为加工钛合金材料的有效手段。

TC4钛合金的超声波振动切削过程是高度复杂的非线性问题，有限元法逐步成为研究振动切削加工机理的重要途径。N.Ahmed[1]建立了超声波振动切削和普通切削Inconel 718的三维有限元模型，对比分析了2种方式下切削力和切削温度分布情况。S.Amini[2]对超声波振动切削IN738进行了有限元分析，重点研究了切削速度、刀具几何参数以及刀具振动幅度对切削过程的影响。杨亮[3]建立了超声波振动切削单晶铜的二维有限元模型，给出了振动过程中应力分布和切削区温度分布的变化规律。易俊杰[4]通过二维正交振动切削模型，对TC4钛合金的振动切削和普通切削进行了对比分析。国内外学者通过有限元法对超声波振动切削已开展一定的研究工作，但在分析振动切削TC4钛合金的残余应力方面仍然不够。由于振动切削具有冲击特性，很有必要对TC4钛合金切削产生的残余应力进行深入分析。

1 切削加工模型及有限元理论

1.1 切削有限元模型

在有限元软件中建立的三维斜角切削模型包含待加工工件和刀具实体模型，待加工工件由工件基体、失效层和切屑层组成，如图1所示。工件材料为钛合金TC4，基体尺寸为2mm×1mm×0.3mm，切屑层和失效层的厚度分别为0.03mm和0.005mm；刀具设为离散刚体，采用材料PCBN，刀具前角为18°，后角为8°，刃倾角λS为10°。工件和刀具采用C3D8T八节点六面体双线性热力耦合单元，分别采用结构化和自由网格划分技术。

图1 斜角振动切削有限元模型Fig.1 FEM model of oblique vibration cutting

1.2 材料本构方程

斜角振动切削是一种具有大变形、高应变率、局部高温特点的动态过程，可采用Johnson-Cook模型描述。该模型综合考虑了加工过程中材料的应变强化效应、应变率强化效应和温度软化作用，定义的本构方程为：

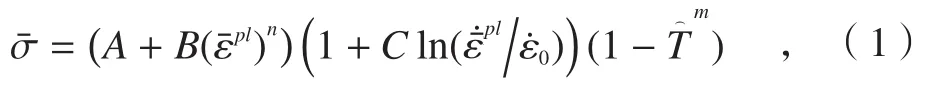
式中，T为当前材料温度，Tr为参考温度，Tm为熔点温度。TC4钛合金材料的5个Johnson-Cook模型常数如表1[5]所示。

表1 TC4的Johnson-Cook模型常数

1.3 材料失效准则

斜角超声波振动切削采用Johnson-Cook材料失效准则，该准则通过失效参数ω判断切屑失效分离情况。当ω＞1时，单元积分点处的材料失效破坏；当单元所有积分点处的材料都失效时，该单元从网格中删除，实现切屑与工件基体分离。材料失效参数ω定义为：

式中,为等效塑性应变增量，是材料失效应变。失效应变的定义为：

式中，d1～d5为失效参数，p为静水压力，q为Mises应力。TC4钛合金材料的单元失效准则参数在表2[5]中给出。

表2 Johnson-Cook失效准则参数

1.4 切削热及热传递模型

在钛合金超声波振动切削过程中，切削热主要来源于切屑剪切区的塑性变形功、前刀面与切屑的摩擦功、后刀面与工件的摩擦功。由于后刀面的摩擦功相对较小，可以忽略不计。在设定钛合金材料均匀且各向同性的条件下，超声波振动切削工件的三维非稳态热传导控制方程为：

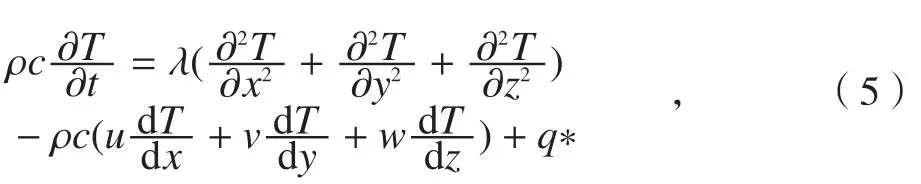
式中，ρ为材料密度，c为比热，λ为热传导系数；x、y和z为笛卡尔坐标，u、v和w为运动热源在x、y、z方向的速度分量；，为塑性变形导致的单位体积热流率；ηp为塑性功转换为热能的系数，一般取值为0.9。振动切削钛合金的热传导过程应考虑热接触和对流换热边界条件：

(1)刀具与切屑的接触摩擦导致的单位面积热流率为qf=ηfτ vchip，其中：ηf为摩擦功转换为热能的系数，一般取值为1.0；τ为接触面的切应力；vchip为接触面相对滑动速度。

(2)刀具前刀面与切屑的接触热传导由qg=kg(θa-θb)式决定，其中：qg为热流密度，kg为间隙热传导系数，θa和θb分别为间隙两边接触物体的温度。

(3)刀具和工件的自由表面与空气的对流换热由式qc=hc(Ts-T0)决定，其中：qc为热流密度，hc为对流换热系数，Ts为刀具或工件的表面温度，T0为周围环境温度。

2 残余应力数值模拟及结果分析

2.1 残余应力数值模拟过程

为研究工件残余应力的大小和分布规律，采用以下3种有对比性的加工模拟方案： (1)施加初始边界条件→普通切削→约束转换→降温冷却； (2)施加初始边界条件→超声波振动切削→约束转换→降温冷却； (3)施加初始边界条件→超声波振动切削→振动时效→约束转换→降温冷却。

在振动切削阶段，工件移动速度为v，刀具振动切削速度vr=Aωcosωt，临界切削速度vc=Aω，速度系数k=v/vc。在振动时效阶段，激振力通过在工件上施加随时间正弦变化的面载荷来模拟[6]。若使工件受力点产生应力释放而又不发生破坏，则动应力σd与残余应力σr之和应大于工件屈服强度σs，同时动应力σd应小于工件疲劳极限σ-1。在约束转换阶段，去除工件的边界条件和接触条件，并通过三点约束法限制工件的刚体运动。在降温冷却阶段，通过设置工件外表面为热交换表面，与外部环境进行对流换热，将工件温度降至与周围环境同温，消除切削热对残余应力的影响。

2.2 结果分析

2.2.1 振动切削对工件残余应力的影响分析

将方案(1)和方案(2)进行对比，研究普通切削和振动切削对残余应力的影响。普通切削时，刀具不动，工件以v=0.5m/s的速度运动；超声波振动切削时，在工件底部加载水平运动速度v=0.5m/s，在刀具刚体参考点处加载振动切削速度，振幅A=10μm，频率f=20kHz，临界切削速度vc=0.628m/s，速度系数k＜1。图2给出振动切削过程中等效应力的分布情况，超声波振动切削的瞬时冲击作用使工件产生很不均衡的应力分布。

图2 切削过程中应力分布Fig.2 Stress distribution in cutting process

如图3所示，在切宽为0.3mm的条件下，普通切削阶段的稳态切削力达到20N，而振动切削阶段的瞬态切削力峰值约为20N。振动切削过程的平均切削力较小，但力加载率非常大，工件受到较强的瞬时冲击。

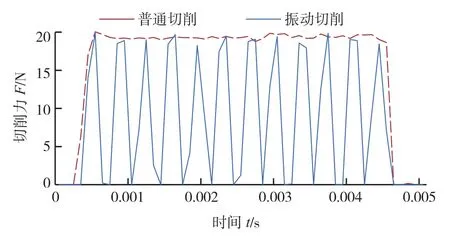
图3 切削力Fig.3 Cutting force

利用2种切削方式去除工件表层材料后，工件沿层深方向的残余应力等值线如图4所示。在普通切削方式下工件沿层深方向的残余应力分布较为均匀，随着距表层距离的增加，残余应力逐渐由表层的拉应力转为压应力，且数值趋于减小；在振动切削方式下工件沿层深方向的应力数值变化范围较大，工件基体的残余应力分布很不均衡，拉应力和压应力夹杂存在，应力梯度变化很大，在工作条件下容易因外界载荷和边界条件变化而引起工件尺寸和形状变化，影响零件疲劳强度和冲击韧性，减弱零件抗疲劳性能。

2.2.2 振动时效对工件残余应力的影响分析

将(2)和(3)进行对比分析，研究振动时效对残余应力的影响。在振动时效阶段，在已加工表面施加随时间正弦变化的激振力，幅值为100MPa，频率为1kHz。沿工件层深方向的应力对比情况如图5所示，振动时效使工件受力部位产生适度的塑性变形，表层残余应力逐步由拉应力转变为压应力，增强零件尺寸稳定性，提高疲劳强度。

图4 不同切削方式下应力等值线Fig.4 Stress contour in different cutting ways

图5 沿工件层深的残余应力分布Fig.5 Residual stress distribution along vertical direction of workpiece

3 结论

(1)超声波振动切削的分离特性，可有效降低平均切削力，改善切削散热条件，提高TC4钛合金工件的加工质量。

(2)超声波振动切削具有的冲击特性，降低了零件的疲劳强度和冲击韧性，使被切削工件表层的应力梯度变化较大，残余应力分布很不均衡，沿层深方向的拉应力和压应力夹杂存在。

(3)在合理的工艺参数下，振动时效能有效地降低和均化超声波振动切削产生的表层残余应力，可在一定程度上提高工件尺寸、形位精度的稳定性以及工件表层的抗疲劳性能。

[1] Ahmed N, Mitrofanov A V, Babitsky V I, et al. Analysis of material response to ultrasonic vibration loading in turning Inconel 718.Materials Science and Engineering, 2006, 424(1/2)： 318-325.

[2] Amini S, Soleimanimehr H. FEM analysis of ultrasonic-vibrationassisted turning and the vibratory tool. Journal of Materials Processing Technology, 2008, 201(1-3)：43-47.

[3] 杨亮, 卢泽生. 精密超声振动切削单晶铜的计算机仿真研究. 系统仿真学报, 2007,19(4)：738-741.

[4] 易俊杰, 刘长毅. 钛合金TC4超声波振动切削有限元仿真.中国制造业信息化, 2008, 37(23)： 29-32.

[5] 吴红兵,刘刚,柯映林,等.钛合金的已加工表面残余应力的数值模拟. 浙江大学学报(工学版), 2007, 41(8)：1389-1393.

[6] 付建科,范万里,陈维壁,等.基于有限元法的重大焊接结构振动时效工艺参数研究.机械设计与制造, 2008(2)：119-121.