浅谈高中数学教学中的两个生成问题
2015-05-30高慧
高慧
在教学中会发现,学生思维的潜力是无限的,在课堂上经常会提出一些预设外的问题,此时,如果顺着学生的思维去探索,就可能有意外的收获——能力的生成.本文着重从在数学活动中生成知识和在数学探究中生成能力两方面探讨了高中数学教学中的生成问题.
一、在数学活动中生成知识
在中学数学课教学中,教学的重点是提高学生的学习能力,因此在教学中要采用多种教学手段以激发学生的学习兴趣,创设活跃的问题情境和指导灵活的学习方法,培养学生的学习能力,帮助学生建构知识.
案例1函数的奇偶性教学片段
师:实际生活中,对称性在许多地方起着极其重要的作用,例如:为保持飞行方向和飞行平稳,火箭的尾翼成中心对称设计;为易于驾驶汽车设计成轴对称等.
(多媒体动画演示)
师:对称也是函数图像的一个重要特征,通过图像的对称我们可以得到函数(函数值变化)的又一个重要性质.
(板书课题:函数的奇偶性)
师:f(x)=x2是同学们非常熟悉的一个函数,下面请大家按照列表、描点、画图的过程画出函数f(x)=x2的图像,并观察分析随自变量的改变函数值的变化特征,说说你有怎样的发现?
生1:如果我将画出的函数图像沿y轴进行翻折,可以发现其图像重合,也就是说f(x)=x2的图像关于y轴对称.
师:很好,生1同学从函数图像角度观察出其图像关于y轴对称,那么,同学们还有其他发现吗?
生2:当自变量x的取值互为相反数时,函数y=f(x)的函数值相等,例如:f(-1)=f(1),f(-2)=f(2)……一般地,当x∈R时,有f(-x)=f(x).
师:很好!从图像上看,函数f(x)=x2关于y轴对称;从数量关系上看,函数f(x)=x2对定义域中的每一个x,都有f(-x)=f(x),我们把具有这种性质的函数叫作偶函数.
(板书偶函数定义)
师:用类似的方法,请同学们对函数f(x)=1x进行研究,能有怎样的发现?
(由此得出奇函数的概念并板书,然后对奇函数与偶函数的定义加以分析)
在上述案例中,笔者通过创设联系实际生活的问题情境,用生活中的对称问题创设情境,让学生动手操作、动脑联想,使学生了解了函数的奇偶性与日常生活实际的紧密联系,明确了研究函数奇偶性的意义和价值.
二、在数学探究中生成能力
在课堂教学过程中,由于师生互动、生生互动而产生更多的信息和创新的火花,尽管是奇谈怪论、异想天开的,但其中很多信息是有价值的,对师生的思维发展具有很大作用.
案例2在高三一轮复习的一堂解析几何课上,笔者提出了这样一个问题让学生思考:
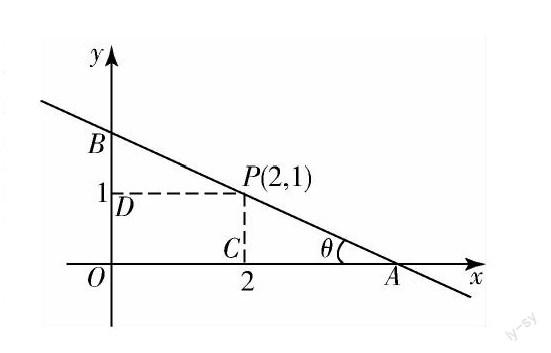
问题:过点P(2,1)作直线l,分别交x轴和y轴正半轴于A,B两点,O为坐标原点,若△AOB面积最小,求直线l的方程.
学生经过思考、探讨后得出以下解法:
解设直线l的方程为y-1=k(x-2).
由题设知k<0,令x=0得y=1-2k;令y=0得x=2k-1k,则S△ABC=122k-1k·(1-2k)=-(2k-1)22k=12(4-4k-1k)=2+(-2k)+-12k≥2+2(-2k)·-12k=4,其中当且仅当-2k=-12k,即k=-12或k=12(舍去)时,(S△ABC)min=4,此时直线l的方程为y-1=-12(x-2),即l:x+2y-4=0.
接着笔者分别对上述解法做了总结点评,正当此题即将讲解结束时,一名学生举起了手,他意外地又提出了一个问题:老师,既然△AOB面积有最小值,我在想线段AB是否有最小值?若有,又是多少?
笔者先前备课可没想到这个问题啊,但是学生突然有这样的问题,便顺水推舟说:“这名同学的问题很好,让我们一起再来探讨,解决这个问题.”接下来的情况让笔者出乎意料,大部分同学把AB用斜率k的函数f(k)=2k-1k2+(1-2k)2来表示,但这个函数式比较复杂,接下来学生无能为力了;少数几名学生受到解法2的启发,引入角度令∠BAO=θ,θ∈0,π2作为自变量,则AB=1sinθ+2cosθ,θ∈0,π2,当笔者把上述两种思路展示后,同学们一致同意后面的一种解法,全班同学又就后面式子的解法探讨起来,最后大家一致同意用导数知识去解决这一问题.当笔者把上述过程讲解完后,同学们运用同样的方法求得了函数f(θ)=asinθ+bcosθ,θ∈0,π2,(a>0,b>0)的最小值,过程略,那么这个函数的最值问题有了一个解析几何的背景,即过第一象限内一点P(a,b)的直线在两坐标轴上截得的线段的最小值问题的解法.至此,由一名学生的意外问题获得了一个精彩的结论.
总之,生成性教学是一种融教学价值观、认识论、知识观与方法论于一体的教学理念,它是对“预成论”教学的一种批判与超越.作为教师,应该创造条件促进教学生成,及时捕捉教学生成的每一个瞬间,不断增强数学教育的时代感、针对性、实效性.
