追击相遇问题的教学设计
2015-05-30李文宾
李文宾

1.教学目标
(1)知识与技能目标。①理解什么是追及和相遇问题。②掌握解决追及和相遇类问题的两个关键——速度相等、位移相等。
(2)过程与方法目标。通过一题多解、多解取优,一题多变、多变归一的研究方法,培养学生发散性思维和创造性思维。
(3)情感、态度与价值观目标。培养学生严谨的科学态度、创造性地思考问题的方法,潜移默化地对学生进行解题规范教育。
(4)教学重点、难点。根据学生的实际情况、个性特点,为了更好地完成本节课教学目标,我设计本节课的重点是:解决追及和相遇问题的基本方法。难点是:速度相等是追上、两物体相距最远和最近的条件。
2.教学分析
(1)教学内容分析。“追及和相遇问题”是高一物理第二章“直线运动”的规律的具体应用,本节课是作为匀变速运动规律的运用特例而编排的。通过本节课的教学,使学生进一步巩固匀变速运动规律的知识,掌握解决追及和相遇类问题的两个关键,为学习牛顿第二定律的两类动力学基本问题奠定基础。
(2)教学对象分析。在学习本节内容之前,学生已经学习掌握了匀变速直线运动及其规律,知道了如何判断物体的运动是否是匀变速直线运动,这都为本节课的教学奠定了基础,但由于追及和相遇类问题涉及的是两个物体的运动关系,这对高一新生来说是一个很难掌握的知识点,因此本节课的教学,我由最简单的追及和相遇类问题入手,一题多解,让学生树立信心,再一题多变,逐渐扩展加深,最终达到通过一道例题将各种追及和相遇类问题联系起来,学生只要掌握了这个例题及变式,在高一遇到的各类追及和相遇问题就都可以迎刃而解。
3.教学方法
(1)教学过程。讨论追及、相遇问题,其实质就是分析讨论两物体在相同时间内能否到达相同空间位置的问题。①两个关系:时间关系、位移关系。②一个条件:两者速度相等。速度相等往往是物体间能否追上、追不上或距离最大、最小的临界条件,也是分析判断的切入点。
(2)解题思路。
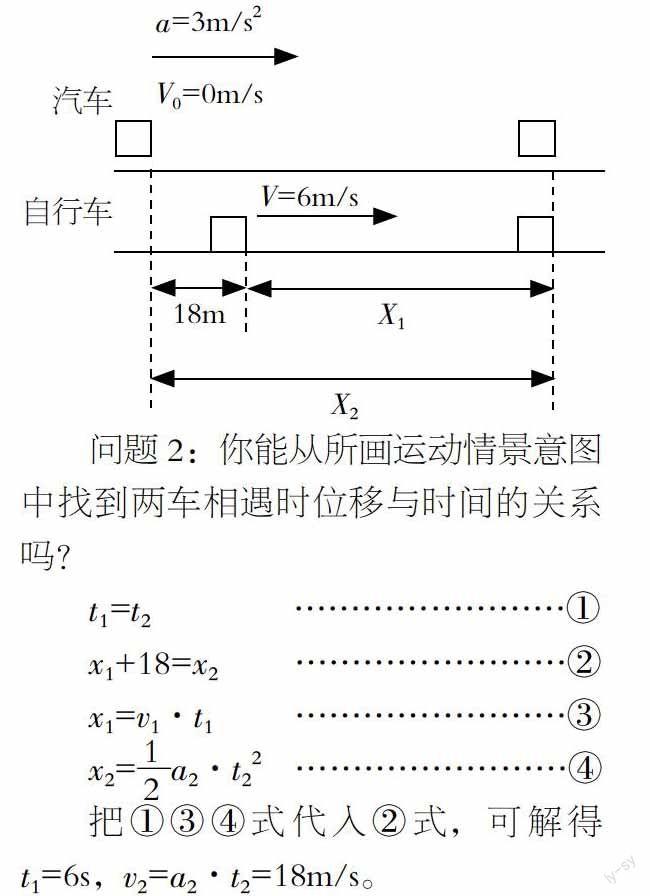
(3)典型例题。例如:匀加速追匀速:一辆汽车在十字路口处等候绿灯,当绿灯亮时汽车以3m/s2的加速度开始行驶。恰在这时一辆自行车在前方18m的同一直线上以6m/s的速度匀速同向运动,试求:①什么时候汽车追上自行车,此时汽车速度是多少?②汽车从路口开始出发后,在追上自行车之前经过多长时间两车相距最远?此时距离多少?
解一:情景分析法
问题1:试分析两车的运动过程,并试着完成运动情景图。
汽车做匀加速运动,自行车做匀速运动,两车开始相距18米。
问题2:你能从所画运动情景意图中找到两车相遇时位移与时间的关系吗?
问题5:你觉得哪一时刻两车相距最远?此时两车速度应有何种关系?你如何计算最远距离?
两车在2s时最远,此时两车速度相等,因此在此之前,自行车速度总大于汽车速度,两车距离不断拉大,至两车速度相等时,距离不再拉大,所以速度相等时,距离最远。
问题6:我们把这种分析情景过程,最终解得答案的方法称为情景分析法,你还有其他方法吗?
引导学生找到两车间距离与时间的函数关系。
提出问题链(让学生讨论完成)。①试在图象中找出0~t1时间内,自行车与汽车的位移,谁大?说明什么?②画出0~t2时间内,自行车与汽车的位移,谁大?③比较t1、t2两个时刻,汽车与自行车的距离如何变化?为什么?④由上面的问题,你能找到自行车与汽车间距离最大的时刻吗?⑤试画出2s~t3时间内,自行车与汽车的位移,谁大?大多少?你能在图象上找到吗?⑥在t3时,两车谁在前?⑦比较0~2s和0~t3两段时间内,两车间的距离如何变化?为什么?⑧汽车在哪一时刻把开始运动后与自行车拉开的距离弥补完?这时汽车追上自行车了吗?⑨汽车追上自行车还要什么条件?你能试着在图象中表现出来吗?
距离最大时:t=2s, ?x=—×6× 2+18=24m
相遇时:18=—×[6+(3·t-6)]×(t-4) t=6s
(作者单位:江苏省南京市高淳县湖滨高级中学)
