基于ANSYS的FSC赛车车架有限元分析

张宇 马健 陈旭

【摘要】中国大学生方程式汽车大赛（简称“中国FSC”）是一项由高等院校汽车工程相关专业在校学生组队参加的汽车设计与制造比赛^[1]。对于非承载式车身的赛车，车架承载着赛车整个车体，车架的结构强度很大程度上影响着整车的安全性、动力性、舒适性、操纵稳定性等多种综合性能。本文对FSC赛车车架进行典型工况下的强度和刚度校核，确定其固有频率及稳定性，并进行疲劳分析，得出车架应力应变结果，为结构的改进提供合理化建议。

【关键词】FSC;ANSYS/Workbench;车架;分析

1 车架有限元模型建立

1.1三维模型导入及网格划分

本文FSC赛车车架采用桁架式结构，在Catia中完成三维模型建立，将其转化成IGS文件导入到ANSYS Workbench中，车架选用4130合金钢，弹性模量为2.11E11Pa，泊松比为0.279，密度为7850 kg·m-3，屈服强度为785MPa，强度极限930MPa。文中将车架的CATIA模型导入到ANSYS Workbench中，进行模型简化处理^[2]。

网格划分是有限元分析前处理中的关键步骤，对后面分析的结果有重要影响。在进行网格划分时，本文对一些主要的受力部位进行网格细化，取1mm的网格大小，对一些非重要受力部位统一采用10mm的网格大小来进行划分，在保证分析精确度的同时还可以提高整个网格分析的效率。划分结果为分成7809个节点，4423个单元^[3]。

2车架工况分析

2.1弯曲工况分析：

弯曲工况是指赛车在满载状态下匀速行驶的状况。计算弯曲工况时，由于车辆行驶的动态效应，车架承受的实际载荷需乘上一个动载因数，一般为 2.0-2.5，本文取2.5，车架静态工况加载方式为：重力场加载800N;座舱底杆集中载荷1875N;发动机固定杆集中载荷2000N;差速器支撑杆集中载荷300N。在分析中忽略对整车分析影响较小的零件，重力加速度取10m/s?^[4]。

通过分析可知，弯曲工况下车架管件所受的最大组合应力为175.35MPa，位于座舱底部，小于屈服极限785MPa。车架的变形主要发生在座舱底部和主环的顶部，最大总变形量为2.0956mm。

2.2紧急转弯工况分析：

赛车在赛道上高速转弯时，由于离心力的作用将受到侧向载荷，此工况下将要求车架具有足够的侧倾稳定性，此处模拟赛车在8字绕环比赛中向左制动转弯的情况，赛道宽3m，由直径是18.25m 的两个圆形赛道组合而成，赛车队在赛车的动力性能计算中得出6秒左右是赛车完成八字绕环单圈所需要的最短时间，我们假设赛车的内侧轮绕直径为16m的圆运动，外侧车轮绕17.5m的圆运动。由向心力的计算公式可知外侧车轮所受向心力与内侧车轮所受向心力的比值为35：32，接近1：1。所以此处近似将赛车所受的侧向向心力平均分布在4个车轮上。取转弯半径为8m，根据上式可求得此时所需的向心力为2381N，乘以动载系数1.5后，总共加载的横向载荷约为3572N。

由仿真分析结果可知，紧急转弯工况下车架的最大应力为171.5MPa，位于座舱底部。车架的最大变形依旧在座舱底部，为2.1858mm左右。

3车架的模态分析

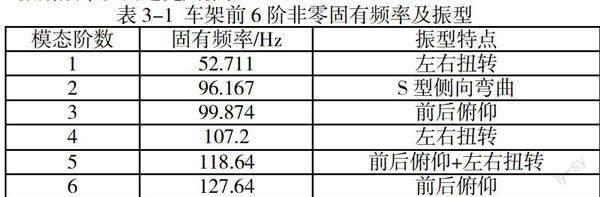
本文应用Ansys workbench 的Modal模塊，在完全固定悬架点的情况下对车架进行非自由模态分析，并设置阶数为六阶，得出车架前六阶的固有频率及对应振型结果如下表3-1所示。

本文赛车选用的发动机为CBR600，怠速转速为1000r/min，怠速频率为33.3Hz，正常转速为5000～7000r/min，频率范围是166.7～233.3Hz。从分析结果可知车架的固有频率能够避开发动机的怠速频率以及正常使用时的频率范围。由于路面对赛车的激励频率低于21Hz，所以车架也可以很好地避开路面的激励频率从而避免共振。

表3-1 车架前6阶非零固有频率及振型

模态阶数

固有频率/Hz

振型特点

1

52.711

左右扭转

2

96.167

S型侧向弯曲

3

99.874

前后俯仰

4

107.2

左右扭转

5

118.64

前后俯仰+左右扭转

6

127.64

前后俯仰

4 车架屈曲分析

屈曲分析主要用于研究结构在特定载荷下的稳定性以及确定结构失稳的临界载荷。本次的赛车车架采用桁架式结构，有一些管件会在特定的状态下受到较大的轴向压力，为了避免在此种压力下造成管件的失稳，所以要进行屈曲分析。

此次屈曲分析主要分析发动机的长固定杆、前环斜撑、主环斜撑以及前环前隔板之间的长底杆，分析时的约束加载同弯曲工况时相同。以发动机的长固定杆为例，首先在发动机的长固定杆上施加100N的单位载荷，由屈曲分析求得的特征值表示屈曲载荷系数，计算的临界线性失稳载荷因子与载荷的乘积，即屈曲载荷=载荷因子×载荷。由于此处施加的载荷为100N，由分析结果可计算出最小的屈曲载荷约为126360N，明显大于发动机实际会受到的载荷施加，所以不会有失稳的情况出现。

5 车架的疲劳分析

疲劳分析是在线性静力学分析之后，通过设计仿真自动执行的。由于在几何方面，疲劳计算只支持体和面，线模型目前还不能输出应力结果，所以疲劳计算对于线是忽略的，所以我们需要对车架模型重新进行简化导入来进行弯曲工况的仿真分析，从而在此静力学分析的基础上进行疲劳分析。从分析结果可以得出，车架座舱底杆和主环及主环附近杆件的寿命及安全系数较低，如果需要增加车架的使用寿命，需要加固相应的杆件。

6 结论

在设计FSAE赛车车架时，应使车架在满足规则及强度要求的前提下，优化车架结构，合理设计刚度，减轻车架自重，降低制造成本。基于对本车架进行的各方面分析结果，根据上述设计原则，该车架可以采取如下方式优化结构：

1）由于车架在各工况下最大应力都远小于材料屈服强度，且有较高的安全系数，故可以适当减少车架杆件壁厚或使用密度相对较小的材料以减轻车架自重。

2）对一些为形成三角结构但并没有承受很大力的杆件可以适当采用细杆来代替，从而更好地实现车架的轻量化。

3）为了提高单位质量下的扭转刚度，在设计车架的结构时应尽量将杆件排布成三角形结构。由于三角形良好的稳定性，可平稳地传递焊接节点间作用力，并减少车架变形。

参考文献：

[1]中国汽车工程协会.中国大学生方程式汽车大赛规则[G].2014.

[2]阳文君，郭振辉.FSC车架静态性能的有限元分析与试验验证[A].湖北：湖北汽车工业学院汽车工程系，2012.

[3]邓泽涵，范正帅，殷行山.基于ABAQUS的FSAE赛车车架有限元分析[A].大连：大连理工大学汽车工程学院，2013.

[4]施长政，师忠秀，柳威，王甜甜.FSC赛车车架的有限元分析[A].山东：青岛大学机电工程学院，2013.