浅析初中数学中全等三角形的教学设计
2015-05-30郑维军
郑维军
老师常说,小学到初中,再到高中,传统的教学方法已经湮灭年轻一代积极主动、善于思考的本性,以致于他们到了大学甚至出了社会工作都缺乏创新的能力,中国不缺乏勤奋苦干的人,缺少的是能开发、会创新的人才。要想彻底突破思想的禁锢,就必须从教学方法开始,老师应该以培养学生的主动思考意识为目的,探索新的教学方式方法。
初中数学是人们生活中不可缺少的一部分。它是开发思维的一门学科,也是学技术的基础,同时也是智力的体现。它可以开发人的智力,培养人的思维能力,挖掘人的内在潜力,提高人们分析问题和解决问题的能力。所以,初中数学教学要求教师一定要引导学生思考,开发学生的思维能力,以培养学生的主动思考意识,如何来培养学生的主动思考意识呢?笔者在多年的初中数学教学中通过实践总结出了一系列经验和方法,最有效的手段是做好一份引导学生的教学设计并实施,本文我以全等三角形为例,如何设计引导学生学习从而达到预期教学目的。
全等三角形是初中几何比较简单的部分,掌握这部分内容是学习三角形相似及四边形的基础,是做一系列复杂证明题必须掌握的,也是整个几何学习的开端。学好全等三角形能引导学生认真、饶有兴趣地学习后面的内容。
(一)教学目标
1.知道什么是全等形、全等三角形及全等三角形的對应元素;
2.知道全等三角形的性质,能用符号正确地表示两个三角形全等;
3.能熟练找出两个全等三角形的对应角、对应边。
(二)教学重点、难点
重点是全等三角形的性质;难点是找全等三角形的对应边、对应角。
(三)教学过程
1.提出问题,创设情境,引导学生主动思考
⑴ 问题:你能发现这两个三角形有什么美妙的关系吗?
这两个三角形是完全重合的。
⑵ 学生自己动手(同桌两名同学配合)
取一张纸,将自己事先准备好的三角板按在纸上,画下图形,照图形裁下来,纸样与三角板形状、大小完全一样。
⑶ 获取概念
通过前面的引导让学生开动大脑用自己的语言叙述:全等形、全等三角形、对应顶点、对应角、对应边,以及有关的数学符号。大概有三分之一的学生踊跃的举手,等他们一个个说出自己的答案之后,我就告诉他们新婚却的答案,这样他们就比较深刻的记住了。
形状与大小都完全相同的两个图形就是全等形。
要是把两个图形放在一起,能够完全重合,就可以说明这两个图形的形状、大小相同。
概括全等形的准确定义:能够完全重合的两个图形叫做全等形。请同学们类推得出全等三角形的概念,并理解对应顶点、对应角、对应边的含义.仔细阅读课本中"全等"符号表示的要求.
2.导入新课
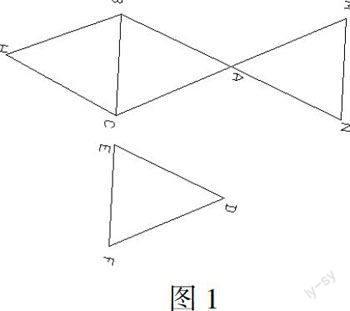
将△ABC沿直线BC平移得△DEF;将△ABC沿BC翻折180°得到△HBC;将△ABC旋转180°得△AMN,如图1所示。
议一议:各图中的两个三角形全等吗? 通过一番激烈的讨论,我们得出的结果是结果是:
△ABC≌△DEF,△ABC≌△HBC,△ABC≌△AMN.
(注意强调书写时对应顶点字母写在对应的位置上)
图1
启示:一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,所以平移、翻折、旋转前后的图形全等,这也是我们通过运动的方法寻求全等的一种策略。
观察与思考:寻找图1中两三角形的对应元素,它们的对应边有什么关系?对应角呢?
引导学生从全等三角形可以完全重合出发找等量关系,从而得到全等三角形的性质:全等三角形的对应边相等.全等三角形的对应角相等。接下来通过三个列子来加强记忆,达到举一反三的目的。同样是学生先思考,然后在黑板上把他们的过程写出来,然后由我来讲。
[例1]如图,△OCA≌△OBD,C和B,A和D是对应顶点,说出这两个三角形中相等的边和角。问题:△OCA≌△OBD,说明这两个三角形可以重合,思考通过怎样变换可以使两三角形重合?
将△OCA翻折可以使△OCA与△OBD重合。因为C和B、A和D是对应顶点,所以C和B重合,A和D重合。∠C=∠B;∠A=∠D;∠AOC=∠DOB。AC=DB;OA=OD;OC=OB。
总结:两个全等的三角形经过一定的转换可以重合.一般是平移、翻转、旋转的方法。
[例2]如图,已知△ABE≌△ACD,∠ADE=∠AED,∠B=∠C,指出其他的对应边和对应角。
分析:对应边和对应角只能从两个三角形中找,所以需将△ABE和△ACD从复杂的图形中分离出来。
根据位置元素来找:有相等元素,它们就是对应元素,然后再依据已知的对应元素找出其余的对应元素。常用方法有:
(1)全等三角形对应角所对的边是对应边;两个对应角所夹的边也是对应边。
(2)全等三角形对应边所对的角是对应角;两条对应边所夹的角是对应角。
解:对应角为∠BAE和∠CAD;对应边为AB与AC、AE与AD、BE与CD。
[例3]已知如图△ABC≌△ADE,试找出对应边、对应角。这个题就由学生讨论完成。 借鉴例2的方法,可以发现∠A=∠A,在两个三角形中∠A的对边分别是BC和DE,所以BC和DE是一组对应边。而AB与AE显然不重合,所以AB与AD是一组对应边,剩下的AC与AE自然是一组对应边了。再根据对应边所对的角是对应角可得∠B与∠D是对应角,∠ACB与∠AED是对应角。所以说对应边为AB与AD、AC与AE、BC与DE.对应角为∠A与∠A、∠B与∠D、∠ACB与∠AED。
做法二:沿A与BC、DE交点O的连线将△ABC翻折
180°后,它正好和△ADE重合。这时就可找到对应边为:AB与AD、AC与AE、BC与DE。对应角为∠A与∠A、∠B与∠D、∠ACB与∠AED。
3.课堂练习
课本练习1。经过上面的讲解,同学们很轻松就完成了这个练习。
4.课时小结
这个环节是非常重要的,它是一个总结概括的行为。所以一定要让同学们亲自说出来,从学习委员开始,经过很多人的补充完善,大家七嘴八舌地就很全面地总结了本次课的内容。通过本节课学习,我们了解了全等的概念,发现了全等三角形的性质,并且利用性质可以找到两个全等三角形的对应元素,这也是这节课大家要重点掌握的。找对应元素的常用方法有两种:
第一、从运动角度看
1.翻转法:找到中心线,沿中心线翻折后能相互重合,从而发现对应元素。
2.旋转法:三角形绕某一点旋转一定角度能与另一三角形重合,从而发现对应元素。
3.平移法:沿某一方向推移使两三角形重合来找对应元素。
第二、根据位置元素来推理
1.全等三角形对应角所对的边是对应边;两个对应角所夹的边是对应边。
2.全等三角形对应边所对的角是对应角;两条对应边所夹的角是对应角。
综上所述,无论在日常的生产和生活中,还是在涉及生存和发展的关键时刻,数学都起着非常重要的作用。通过教学方案的设计,创设问题情境,引导学生自主思考,使学生开动大脑跟随老师的教学积极回答问题。从而使学生养成积极主动思考问题的习惯,为以后的学习和工作奠定思维基础。培养学生积极主动地思意思不仅有利于个人的学习和工作,也是素质教育的要求,高全民族的数学素质,培养具有创新能力的人才,更是我们初中数学基础教育应有的教学元素。
