空间微动目标高分辨成像方法研究

宋扬 魏建新 郭世伟

【摘要】 对于空间微动目标，本文介绍了三种微动形式及现有的ISAR成像方法，针对滑动散射点模型的单个进动锥体，根据其回波模型提出一种基于复数后向投影的高分辨成像方法，并进行仿真实验以验证算法的可行性。

【关键词】 微动 进动锥体 复数后向投影

一、引言

对于空间运动目标，除质心平动外往往还伴随着小幅振动、转动和其他高阶运动，称为微动，微动定义为目标或目标构件在径向相对雷达的小幅非匀速运动。空间目标的微动形态主要有自旋、进动和章动。自旋是指目标绕自身主轴以一定角速度进行的旋转运动；进动是指目标除了绕其主轴做自旋运动之外，还以一定角速度绕锥旋轴做锥旋运动；章动是指目标在进动的过程中，进动角随时间做周期性变化的一种运动。

由于微动的非平稳性，使得现有的成像方法（如RD）失效，现有的文献中，空间目标ISAR成像方法大致有以下几种：一是基于经验模态分解的方法对微动目标旋转部件的成像[1，3]。二是基于后向投影的成像方法，对自旋目标进行了高分辨成像[2]。三是基于正交匹配追踪的自旋目标窄带雷达成像算法[4]。

针对真实目标可能存在的滑动散射点，在第2部分建立滑动散射点模型，基于复数后向投影算法，对其距离慢时间回波进行相干积累，从而实现高分辨成像。

二、基于复数后向投影的高分辨成像方法

在实际问题中往往会遇到滑动散射点的情况，滑动散射点是指散射点位置随雷达视线变化的散射点。下面以光滑锥体为例，建立光滑锥体的进动模型，研究基于复数后向投影的成像算法。

2.1回波模型

光滑进动锥体目标为旋转对称体，其自旋运动并不影响回波的散射特性，这里只考虑锥旋运动。如果雷达发射LFM信号，则在f-tm域，进动锥体的回波为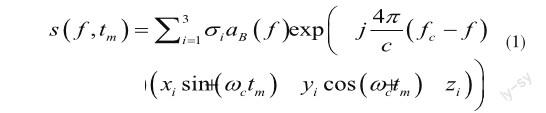

其中B是信号带宽，aB（f）是宽度为B的矩形窗，当|f|≤B/2时，aB（f）为1，否则为0， f表示距离频率，σi为第i个散射点的后向散射系数，fc为载频，c为光速。从式（1）可以看出，光滑进动锥体上三个特征散射点对应的回波包络和相位均为正弦曲线。

这里假设锥体的旋转周期能够准确估计。式（1）描述的回波包络在距离慢时间域为正弦曲线，该曲线在距离慢时间信号中的形状及位置是由散射点位置参数（xi，yi，zi）决定的。如果能对各条曲线加以拟合则可得到曲线信息，也就相应得到了散射点的位置信息。散射点三维坐标主要通过下面关系式决定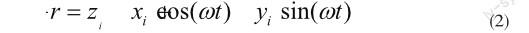

利用旋转点目标回波在距离慢时间域的周期性变化规律，通过拟合正弦曲线就可估计散射点空间位置信息，从而可以进行成像。

2.2成像算法及仿真实验

复数后向投影算法的表达式为：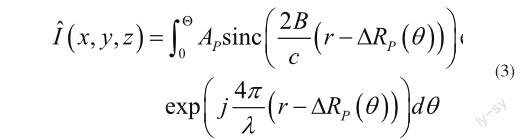

其中r=xsinθ+ycosθ+z。可以看出，式（3）描述的算法沿不同的正弦曲线进行相干积分。以散射点P为例，当x=xP，y=yP，z=zP时，相位项被匹配为0，而被积分项的幅度则变为AP。因此，参数域（x，y，z）的峰值点位置将对应散射点的坐标（xP，yP，zP）。具体的成像算法步骤为：

Step1：通過距离压缩来获得距离-慢时间域回波；

Step2：对Step1的数据按照式（3）沿不同的正弦曲线进行相干积分；

Step3：对Step2的结果，取出不同的x，y，z对应复数后向投影的最大值，进行成像。

下面采用电磁仿真数据的仿真实验来验证算法的有效性。电磁数据的仿真模型为：弹头为对称圆锥体，锥体高度0.96m，底面半径0.25m，锥顶为圆弧型，半径为0.01m，下文使用的仿真数据是HH极化数据。仿真实验进动角为5°，仿真结果如图1和图2：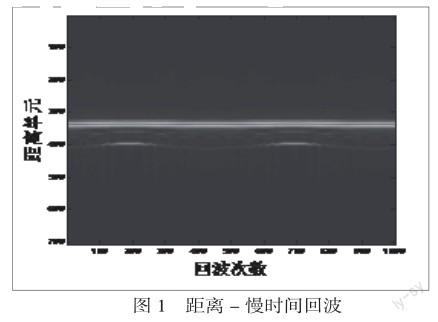

对于上述仿真结果，图1为距离慢时间回波；图2是在复数后向投影算法的基础上合成的图像，其中合成的图像是指分别搜索锥顶和锥底两个散射点的位置，然后幅度归一化后合成到一幅二维图中的结果，验证了算法的可行性。

三、结束语

本文主要研究了空间微动目标的高分辨成像方法，首先介绍了锥体自旋、进动和章动三种微动形式；对于实际存在的滑动散射点，本文提出了一种基于复数后向投影的高分辨成像方法，对于速度已经完全补偿的目标，通过对其距离慢时间回波的相干积累，从而实现高分辨成像。

未补偿速度的光滑锥体多目标高分辨成像将是下一步的研究的方向。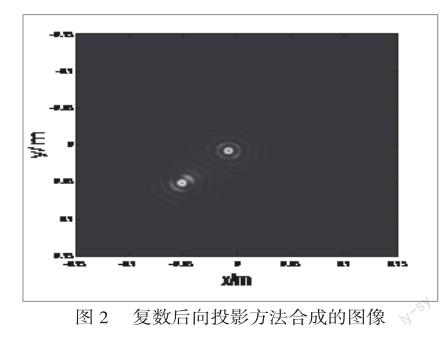

参 考 文 献

[1] Bai Xueru， Xing Mengdao， Zhou Feng， Lu Guangyue， Bao Zheng. Imaging of micromotion targets with rotating parts based on empirical-mode decomposition. IEEE Transactions on Geoscience and Remote Sensing. Nov. 2008， Vol. 46（11）. 3514-3523.

[2] Bai Xueru， Xing Mengdao， Zhou Feng， Bao Zheng. High-resolution three-dimensional imaging of spinning space debris. IEEE Transactions on Geoscience and Remote Sensing. Jul. 2009， Vol. 47（4）. 2352-2362.

[3] 白雪茹， 周峰， 邢孟道， 保铮. 空中微动旋转目标的二维ISAR成像算法. 电子学报，2009年9月，Vol. 37（9）. 1937-1943.

[4] Bai Xueru， Sun Guangcai， Wu Qisong， Xing Mengdao， Bao Zheng. Narrow-band radar imaging of spinning targets. SCIENCE CHINA Information Sciences. Apr. 2011. Vol. 54（4）. 873-883.