基于运输问题的求解方法探讨

段连伟　牛凤秋　刘芬

[摘要]运输问题是运筹学的一个分支，是线性规划的特殊形式。它研究的是如何在一个大物资调运中，制定出一个由若干个产地将物资根据已知的运输交通网运到各个销售地的方案，使得总运费最小。利用Matlab依据遗传算法的理论来计算出最佳结果是很有必要的，文章以运输问题为例阐述了基于Matlab 的定量分析方法，解决了运输最优方案求解这一大难题，可以广泛应用于物流配送领域。

[关键词]Matlab；遗传算法；产销平衡；产销不平衡；表上作业法

[DOI]1013939/jcnkizgsc201533073

1问题陈述和正文内容

运输是物流功能中最基本的功能。为了降低物流成本，我们有必要研究物流运输中如何组织物资调运才能使总运输成本最低这一重要问题。利用Matlab优化工具箱，可以求解线性、非线性、多目标和二次规划等大中型问题，为优化方法在工程中的实际应用提供了更快捷的途径。

在Matlab中构建函数l（x）解决线性规划问题。运输问题的最优解本质属于极值问题，极大值问题的求解可以转化为极小值问题，因此在Matlab中以求极小值为标准形式，构建的函数l（x）的具体格式如下：

[X，v，e，o，l]=l（F，A，b，m，n，M，N，P，Z）。

式中：X为问题的解向量；F为由目标函数的系数构成的向量；A为一個矩阵；b为一个向量，表示线性规划中不等式约束条件，A，b是系数矩阵和右端向量；m和n为线性规划中等式约束条件中的系数矩阵和右端向量；M和N为约束变量的下界和上界向量；P为给定的变量的初始值；Z为控制规划过程的参数系列；v为优化结束后得到的目标函数值。e=0表示优化结果已经超过了函数的估计值或者已声明的最大迭代次数，e>0表示优化过程中变量收敛于解X，e<0表示计算不收敛。

Matlab处理矩阵运算的强大功能编写遗传算法程序有着巨大的优势，它们结合的原理步骤如下：

（1）编码：采用二进制编码方案，用二进制数构成的符号串表示个体，然后随机产生一个初始种群。

（2）解码：编码后的个体构成的种群须经过解码转换成原问题空间的决策变量构成的种群，之后才能计算相应的适应值。

（3）选择与交叉：选择过程是利用解码后求得的各个体适应值大小，淘汰一些较差的个体而选择出一些比较优良的个体，选择产生的新个体重新配对，形成新的交配对象。

（4）变异：对于二进制的基因串，变异操作就是按照变异概率随机选择变异点，在变异点处取反。

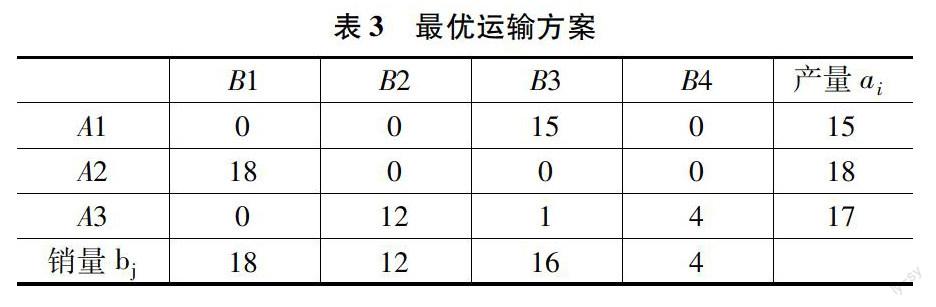
2实例分析

针对产销不平衡问题，核心方法是将产销不平衡转换为产销平衡的情形，然后进行求解。

（1）对于“产>销”情形：可虚拟一个销售地（库存），让多余的产量均运抵此销售地，则其销售量=“产-销”，同时令该虚拟的销售地的单位运价为0；

（2）对于“销>产”，可虚拟一个产地，让其产量=“销-产”，同时令该虚拟的产地的单位运价为0。

对于这个实际问题，虚设一销地，令其销量为产销量之差：B4=ai-bj=4。该列单位运价为0，即可化为产销平衡问题。如表1所示。

3结论

在物流运输中运用Matlab软件，借助遗传算法的思想，解决运输线路的优化问题，简化了复杂的运输过程，提高了运输规划的效果。且能寻找出物流运输方案的最优解，从而降低物流成本，使得一些公司在物流上的投资可以进行优化，赢得更多的效益。