广义线性模型及其在车险定价中的应用

摘 要：文章简单分析了传统非寿险精算方法存在的缺陷，引入了非寿险精算的经典模型——广义线性模型，并通过R语言对实例进行了分析，并给出广义线性模型在车险定价中的一般步骤。

关键词：非寿险；广义线性模型；车险定价

广义线性模型（Generalized Linear Models，简称GLM）是1972年由Nelder和Wedderburn提出的，通过对经典线性回归模型进行了进一步的推广，建立了统一的理论和计算框架，推进了回归模型在统计学中的发展。继20世纪80年代Nelder和MaCullagh将GLM引入到精算学后，20世纪90年代，英国的精算师首次将广义线性模型引入到非寿险定价中，这大大解决了传统的非寿险定价方法--单项分析法所面临的局限性，直至现在汽车保险和商业保险等非寿险仍旧使用这一方法。近年来，GLM在理论和应用方面都得到了快速的发展，包括在拓展模型，模型的诊断以及参数估计方法等方面的研究都不断趋近于成熟，适用与GLM的计算机软件也日益增多，包含GLM专用程序GLIM（Genneralized Linear Interactive Modelling），SAS统计软件（Genmod模块），统计软件R中相应的程序包也可以完成GLM常见模型的估计和假设检验问题。在中国车险定价中，得益于保监会在2010年出台的《关于在深圳开展商业车险定价机制改革试点的通知》，为广义线性模型在车险定价方面提供了制度上的保障。

1 传统的非寿险定价方法

1.1 单项分析法（One-Way Analysis）

单项分析法是指每次仅计算一个费率因子对其保险产品价格的影响。由于忽略各个费率因子之间的相互关系，容易导致定价结果的严重扭曲，只有当各个费率因子之间是相互独立的，这种方法所得到的结论才是稳定可靠的。例如，在汽车保险定价中，对车龄进行单项分析，结果表明汽车时间越长，保险成本越高。但是导致这一现象的很大原因可能是女性驾驶员驾驶旧车，这才导致了旧车的保险成本较高。而根据车龄和驾驶员性别的单项分析结果来厘定车险费率，将会重复使用驾驶员性别对车险费率的影响，导致对女性驾驶员收取过高的保险费。在竞争日益激烈的非寿险市场下，单项分析这一传统方法明显过于简单。

1.2 最小偏差法（Minimum Bias Method）

最小偏差法是19世纪60年代发展的一种分类费率厘定的方法，可同时确定两个或两个以上分类变量的相对费率。这一方法需要通过方程组建立损失数据和各个费率因子之间的关系，通过迭代的方法求解未知参数的最优解。在仅有两个费率因子的情况下，

其中eij为费率单元（i，j）的风险单位数，mij为权数，？琢i，？茁i分别为相应费率因子在不同水平的相对费率，yij为观测值。相比于单项分析法，最小偏差法虽然解决了因忽略各费率因子之间的相互关系所可能导致的定价结果扭曲，但是仅有两个费率因子的情况下，迭代都是十分复杂的，更何况实际情况下不止两个费率因子，所以这一方法依然无法形成一个完整的统计框架。

2 广义线性模型（GLM）基本理论

广义线性模型可以解决以上两种传统方法存在的问题，同时考虑多个费率因子，并处理整个指数族分布。广义线性模型基于传统的线性回归模型的一系列假设之上，放宽对这些假设的要求，广义线性模型的假设一般由三部分组成：随机成分、系统成分和连结函数。

2.1 随机成分

随机成分是指因变量Y或误差项的概率分布。y1，y2，…，yn是因变量Y的相互独立样本，服从指数分布族的其中一种分布，指数分布族包含正态分布、泊松分布、伽马分布、逆高斯分布等分布。指数分布族的概率密度为：

2.3 连结函数

连结函数是人们在一般线性模型中常常忽略的部分，在一般线性模型中连结函数是单位连结函数，而广义线性模型的连结函数是严格单调并可微的，将变量Y的期望与系统成分连接起来，此时E（Y）=g-1（？浊），这里g是一个单调可微的函数。

文章主要通过R软件的相关函数，完成广义线性模型的相关统计分析，鉴于篇幅有限，相关程序代码就不一一列出，只给出模型检验的最终结果。

3 广义线性模型的实证分析

3.1 数据说明及模型构建

广义线性模型对数据量的要求较大，这是要保证较多风险类别对结果影响的可信度，所以广义线性模型一般使用原始数据，文章采用某保险公司公开的机动车第三方责任险数据，可从网站（www.statsci.org）上直接下载。样本数据共有7个变量，我们考虑4个影响索赔额的费率因子：

（1）年均里程数kilometres，共分5个水平：K1，K2，K3，K4，K5；（2）行车区域zones，共分7个水平：Z1，Z2，Z3，Z4，Z5，Z6，Z7；（3）无赔款折扣等级bonus，共分7个水平：B1，B2，B3，B4，B5，B6，B7；（4）车型make，共分9个水平：M1，M2，M3，M4，M5，M6，M7，M8，M9。

此样本共有5×7×7×9=2205个风险类别，除去23个风险暴露数（没有被保险人）为0的，剩下2182个风险类别。

我们首先对索赔次数和索赔额进行了传统的多元线性回归，结果发现索赔次数和索赔强度的拟合结果出现了负值，这显然是不合理的。

下面建立广义线性模型，

这里Yijkl和mijkl分别表示单元（i，j，k，l）的索赔强度和索赔次数，i，j，k，l分别代表上述4个费率因子的各个水平，即i=1，2，…，5，j=1，2，…，7，k=1，2，…，7，l=1，2，…，9。

由于索赔次数的建模方式与索赔强度一致，此处就不再重复表达。由索赔频率=索赔次数/风险暴露数，可以得到索赔频率的结果，则纯保费为索赔频率的期望与索赔强度期望的乘积。

3.2 对模型进行实证分析

（1）索赔次数

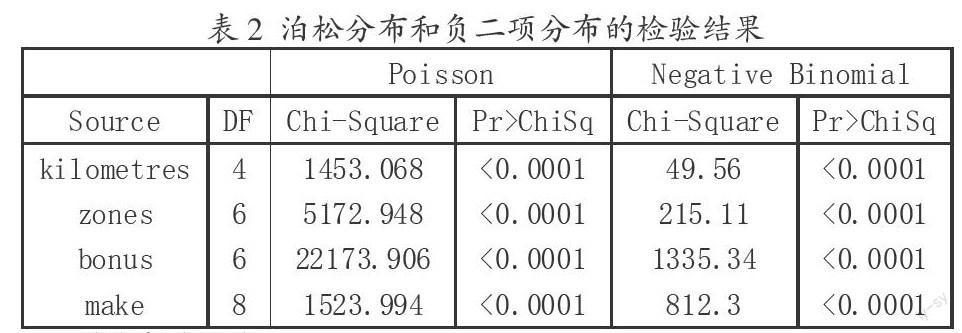
在估计索赔次数时，常用泊松分布和负二项分布假设下，用对数连结函数建立广义线性模型，这是为了保证各个费率因子之间是乘积关系。下面运用R软件的glm（）语句对数据进行拟合（表1），从表中可以看到负二项分布的离差小，对数似然值大，AIC值小，表明负二项分布的拟合优度较好。

（2）索赔强度

在估计索赔强度时，常用伽马分布和逆高斯分布假设下，用对数连结函数建立广义线性模型。下面运用R软件的glm（）语句对数据进行拟合（表3），从表中可以看出伽马分布的离差小，对数似然值和AIC与逆高斯分布的AIC值相差不大，可知伽马分布假设下的模型拟合效果相对较好。

3.3 结束语

根据模型的拟合效果，我们选择负二项分布GLM对索赔次数进行分析，选择伽马分布GLM对索赔强度进行分析。在实证分析中我们发现，有些费率等级拟合效果并不显著，可考虑将进行等级的合并，精算师在实际运用广义线性模型进行费率厘定时，应充分考虑建模本身的风险，模型参数的风险以及随机误差的风险等。目前，随着广义线性模型不断程度的加深应用，多种统计软件也日益完善成熟，鉴于R软件不断更新，包含GLM以及GLM的许多拓展模型如：GAM，GAMLSS等，也可以在R中找到相关函数，可通过www.jstatsoft.org找到最新研究成果。

参考文献

[1]王新军，王亚娟.基于广义线性模型的车险费率费率厘定研究[J].保险研究，2013（9）：43-56.

[2]张连增，吕定海.广义线性模型在非寿险费率分析中的应用[J].数理统计与管理，2013，32（5）.

[3]孟生旺.广义线性模型在汽车保险定价的应用[J].数理统计与管理，2007，26（1）.

[4]薛毅，陈立萍.统计建模与R软件[M].北京：清华大学出版社，2007.

[5]De Jong P，Heller G.Generalized Linear Models for Insurance Data[M].New York：Cambridge University Press，2008.

[6]McCullagh P，Nelder J A.Generalized Linear Models[M].Londen： Chapman&Hall，1989.

作者简介：张天舒（1991-），女，满族，辽宁省兴城市，辽宁师范大学，硕士，应用统计。