强度参数统计特性对边坡稳定可靠性的影响

桂勇　罗嗣海　邓通发

摘要：由于对边坡强度参数统计特性考虑不全面，使得边坡可靠性指标计算值偏小，对应的失效概率偏大，常常超过10%，设计中难以采纳，造成地基可靠度规范的制定和执行进展缓慢。以某高速公路全风化花岗岩土质高边坡为工程背景，在分析土质参数统计特性的基础上，采用极限平衡理论和蒙特卡罗模拟法，系统地分析了土质强度参数的均值不定性、变异性、相关性、区间特性和空间变化性等对边坡稳定可靠性的影响。结果表明：土性参数的各种统计特性对边坡稳定可靠性均具有不同程度的影响。可靠性指标计算值随抽样距离的减小而增加，随c或φ均值的增大而增加，随c和φ的变异系数的增大而减小，随c和φ相关系数绝对值的增大而增加，考虑区间性后可靠性指标计算值也明显变大。即变异性对边坡稳定不利，而相关性、区间性和空间变化性对边坡稳定有利。因此，准确而全面地考虑土质参数的统计特性，尤其是在参数变异性和相关性的基础上加以考虑土性参数空间变化性和区间性会更加符合工程实际，且计算结果趋于安全，有利于地基可靠度规范的推广运用和边坡工程的安全评价。

关键词：边坡稳定可靠性；强度参数；统计特性；区间性；空间变化性

中图分类号：TU 443 文献标志码：A 文章编号：1674-4764（2015）04-0067-10

Abstract： Without comprehensive consideration of the strength parameters statistical properties， the slope reliability index calculation value become smaller and the failure probability become larger， often more than 10%， which was difficult to adopt in design.Hence， the foundation reliability norms formulate and implement made slow progress. Take a completely weathered granite soil slope of an expressway as engineering background， and based on the analysis of the statistical characteristics of soil parameters， the limit equilibrium theory and monte carlo simulation method were used to systematically analyze the soil strength parameters mean uncertainty， variability， correlation and interval characteristics and spatial variability of impact on the reliability of the slope stability. The results showed that all kinds of statistical features of soil parameters had varying degrees impact on slope stability reliability. The reliability index calculation value increased with the decrease of the sampling distance， increased with the increase of the mean values of

c or φ， decreased with the increase of the variation coefficientc and φ， increased with the increase of the correlation coefficient absolute value of c and φ， and the reliability index calculation value became obvious bigger when interval characteristics were considered. The findings indicated that variability was adverse to the slope stability and the correlation， interval characteristics and spatial variability were good for the slope stability. Therefore， with accurate and comprehensive consideration of the soil parameters statistical features， especially with the consideration of space variability and interval characteristics on the basis of the consideration of parameters variability and correlation will be more in line with the engineering practice， and the calculation results tend to be more reliable. It is advantageous to the adopt reliability norm and safety evaluation of slope engineering.

Key words： slope stability reliability， strength parameters， statistical property， interval， spatial variability

边坡系统具有显著的模糊性和不确定性，影响边坡稳定的因素也常常是不确定的，定值法分析没有考虑这种特性，结果往往偏于危险，比如，安全系数大于设计规范值的边坡也有可能失稳[1，6]，具有相同安全系数的边坡，其可靠性却可能不一样[2]。可靠度分析是一种基于概率论理论的分析结构物安全程度的分析方法，能够有效地考虑边坡系统内实际存在的变异性和相关性，能够说明“边坡有多稳”。

20世纪70年代以来，在各类工程结构的设计中全面引入了概率极限状态的设计原则和方法，但由于对边坡土质强度参数统计特性的考虑不全面，使得可靠性指标计算值偏小，失效概率计算值偏大，往往超过10%，设计中难以采纳，即使对已证明是安全稳定的边坡工程也是如此[3]。这种理论与实际相背离的情况使得目前国内外对于地基可靠度规范的制定和执行进展缓慢[3]，因此，系统地分析土质强度参数统计特性对边坡稳定可靠性的影响具有重要的理论意义和实践价值。

不少学者对此进行了研究，取得了一些研究成果。陈鹏等[4]基于因素敏感性采用Rosenblueth法进行边坡稳定可靠性分析，发现将敏感性较大的因素作为随机变量时所得的破坏概率较大，且其变异性也会对结果产生重大影响。李宗坤等[5]探讨了参数c、φ的相关性和变异性对土石坝边坡稳定可靠性的影响，得出参数负相关性对坝坡稳定有利而参数变异性对坝坡稳定不利的结论。李萍等[6]基于点估计法进行了黄土边坡可靠性分析，发现强度参数的变异性是影响边坡失效概率大小的主要因素。蒋水华等[7]采用Sarma法和随机响应面法进行边坡稳定可靠性分析，发现潜在滑体的可靠指标随着c、φ间负相关性增加而增大。谭晓慧等[8]采用有限元法和Mohr-Coulomb屈服准则分析了参数离散性和相關性等对边坡稳定性的影响，发现c、φ对可靠性指标的相对影响比其他参数的影响要大得多，并且随着c、φ间负相关系数的增加，其对可靠性指标的相对影响也相应增加。朱红霞等[3]基于随机场理论和方差折减函数进行了天津港口边坡可靠度分析，发现φ的变异性对可靠度指标的影响较c更为敏感。郑敏洲等[9]采用Excel规划求解工具分析了花岗岩残积土边坡稳定可靠性，结果表明边坡稳定可靠度不仅与土体参数的均值有关，而且与其相关性和变异性有关，且变量的相关性对可靠度影响较大。陈群等[10]分析了土石坝坝料强度参数的均值不定性、相关性和变异性对坝坡失稳概率的影响，表明失稳概率随土质强度参数均值的增大而减小，随变异系数的增大而增大，并且两个强度参数的相关性对坝坡的失稳概率也有影响显著。

不难看出，现有的研究着重于强度参数的变异性和相关性对稳定可靠性的影响上，而对强度参数的其他统计特性，如参数的区间特性和空间变化性则缺乏考虑。以某高速公路全风化花岗岩土质高边坡为工程背景，在分析土质参数统计特性的基础上，利用极限平衡理论和蒙特卡罗模拟法，系统地分析了土质强度参数的均值不定性、变异性、相关性、区间特性和空间变化性等统计特性对边坡稳定可靠性的影响。

1 理论分析

1.1 蒙特卡罗法基本原理

可靠度计算方法主要有一次二阶矩法、Rosenbluth点估计法和蒙特卡罗法等[11-14]。其中蒙特卡罗模拟法是以数理统计原理为基础的一种抽样计算理论，该法回避了可靠度分析中数学上的困难，且不受分析条件的限制，随机变量可以具有任意分布的特点，只要模拟的次数足够的多，计算精度就能相对的高，因此，蒙特卡罗模拟法在许多领域均具有广泛的应用。蒙特卡罗法假定随机变量的概率分布以及变量之间的相关结构都是已知的，生成足够多组服从给定概率分布规律的随机变量数据。然后对每组随机变量分别运行数值模型，再用数理统计的方法评价这些随机变量所对应的模拟结果即可获得模拟结果的可靠度。其用于边坡稳定可靠度分析的基本原理如下：

2 算例分析

2.1 工程概况

计算实例边坡位于大庆至广州高速公路江西里仁至龙南段K53+190左坡，该地区地质情况详见文献[15]。边坡共分为5阶，前4阶坡高为8 m，第5阶坡高7.5 m，边坡总高39.5 m。前3阶坡度为1∶1，后2阶坡度为1∶1.25。采用有限元软件Geostudio的Slope/W和Seep/W模块进行分析，并考虑了地下水位的影响，以年均降雨量为0.3 mm/h的稳态渗流计算结果作为地下水分布的初始状态。即先用Seep/W模块进行稳态渗流分析，再将其结果导入Slope/W模块进行边坡稳定可靠度分析。有限元模型见图2，初始压力水头分布见图3，模型共计5 000个单元和5 034个节点。

2.2 全风化花岗岩强度参数统计特性

由于地基中不同地点的岩土在成土环境、矿物成分、颗粒级配组成和应力历史等方面存在差异，造成地基土中点与点之间的土性会存在不同程度的差异，这种差异在空间上一般表现为渐变性。同时，在土质强度参数测量中，由于试验设备和操作人员的不同，加上存在人为扰动和试验误差，土性参数测试条件与实际情况有出入等因素会导致测量参数的离散性。试验表明，土性指标与其所处的空间位置密切相关，即土层中任意两点的同一参数指标（如相邻土体φ与φ、c与c之间）存在自相关性，土层中同一点的不同参数指标（如相同土体的c和φ之间）存在互相关性[16]，且其相关系数的大小在-0.72～0.35之间[17]，这种相关性会随着地基中两点间距离的增大而逐渐减弱，当超过一定的距离后便可认为参数的相关性为0，从而使得土性指标表现出空间变化性。

背景工程边坡岩土体为全风化花岗岩，简化等效为各向同性连续介质。根据现场钻孔资料和室内实验统计资料，边坡土体的饱和渗透系数为2.1×10-4 cm/s，饱和含水率为37.5%，残余含水率为11.9%，重度为19.2 kN/m3，黏聚力c和内摩擦角φ视为符合正态分布随机变量，其统计特性见表1。

3 计算结果及分析

3.1 空间变化性的影响

参数相关性会随着地基中两点间距离的增大而逐渐减弱，当超过一定的距离后便可认为参数的相关性为0，即此时参数各自独立，因此，当边坡的潜在滑动面长度显著且材料单一时，空间变化性就显得尤为重要。图4为背景工程边坡的典型滑动面，在进行蒙特卡罗抽样试验时，有3种处理方法：1）对整个滑面的每一层土的参数只取样一次；2）沿着滑面对每个土条的参数取样；3）沿着滑面，每间隔一定抽样距离取样土的参数。方法1）实际上没有考虑土质参数的空间变化性，方法2）取样间距过小，人为地将空间变化性考虑过大，因此，对土只取样一次和对每个土条都取样一次都不太符合实际，间隔一定的距离取样的方法3）比较合适，但方法1）、2）可以用来计算失效概率的上、下限范围。

为了研究土性参数空间变化性对边坡稳定可靠性的影响，不考虑表1参数取值的区间特性，取黏聚力c和内摩擦角φ为符合正态分布的随机变量，计算不同抽样距离下边坡稳定可靠性指标，得到可靠性指标随抽样距离的变化曲线（图5），从图中可见，随着抽样距离的增加，可靠性指标总体趋势是下降的，一开始急剧下降，随后下降趋势变缓，最后趋于一个定值。另外，可靠性指标的变化范围较大，为区间[1.775，9.078]，由此可见，土性参数空间变化性对边坡稳定可靠性具有较大的影响，考虑空间变化性有利于边坡的稳定，正确认识和模拟空间变化性是正确采用可靠度计算边坡稳定性的前提。

根据背景工程的钻孔资料和室内实验统计资料，本边坡的抽样距离取8 m（即下面的分析均按8 m计算），计算的边坡稳定系数为1.061，失稳概率为0，可靠性指标为5.295，边坡处于稳定状态，但由于计算稳定系数小于1.2，故设计中采用了一定的工程防护措施和防排水措施。

3.2 区间性的影响

从表1可知，试验得来的土质参数具有最小值和最大值，即在一个区间范围内，边坡可靠度研究应可虑这个特点才更加符合工程实际。以表1中黏聚力c为例，c的概率分布密度曲线在不考虑区间和考虑区间两种情况下是有很大差异的，分别见图6和图7。为了研究土质参数区间性对边坡稳定可靠性的影响，在后面的分析中，均分考虑区间性和不考虑区间性两种情况进行了对比计算，计算结果及分析见下文。

3.3 均值的影响

保持黏聚力c和内摩擦角φ的变异系数不变，分别改变各自的均值μ进行边坡稳定性概率分析。在表1参数基准均值的基础上，分别减小1倍、2倍和3倍标准差，增大1倍、2倍标准差，共获得6组不同的均值数据，并分考虑区间和不考虑区间两种情况分别计算。计算工况和结果如表2所示，边坡的失效概率和可靠性指标随参数均值的变化曲线见图8和图9。

由图可知，当c和φ的变异系数不变时，边坡的失稳概率随c或φ的均值的增大而减小，可靠性指标随c或φ的均值的增大而增大。其中，φ的均值对边坡稳定性指标的影响要比c的均值的影响大，即φ的边坡稳定敏感性要比c大。从参数区间性来看，区间性考虑与否对边坡的失稳概率的影响不大，但对可靠性指标的影响较大，考虑区间性后，失效概率和可靠性指标随參数均值的变化曲线变得更陡，即区间性使得均值对边坡稳定性的影响更加灵敏。

从表2中计算结果可知，c和φ的均值对概率分析所得的安全系数的均值影响较大，安全系数的均值随c和φ的均值的增大而增大。

3.4 变异性的影响

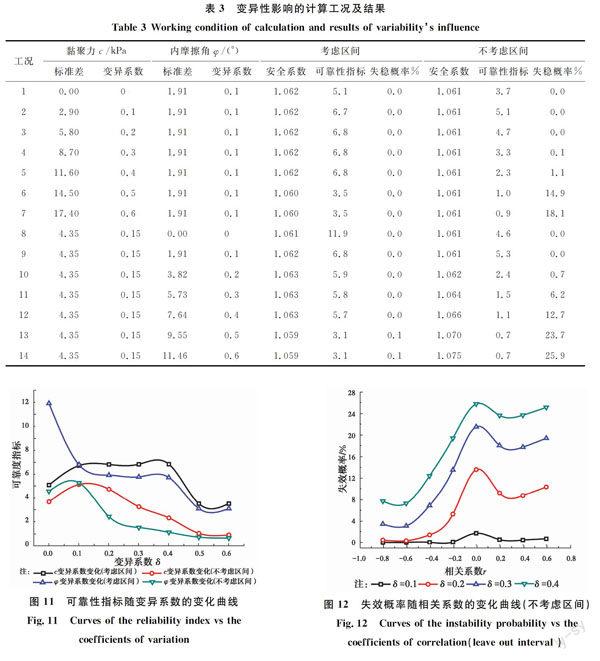
保持参数c和φ的均值不变，分别改变各自的变异系数进行边坡稳定可靠性概率分析，并分考虑区间和不考虑区间两种情况分别计算，计算工况及结果见表3。边坡的失稳概率和可靠性指标随c和φ的变异系数的变化曲线见图10和图11。由图可知，在c和φ的均值不变的情况下，当不考虑区间时，边坡的失稳概率随c和φ的变异系数的增大而增大，其中φ的变异系数对边坡失稳概率的影响比c的变异系数的影响大，可靠性指标总体趋势是随c和φ的变异系数的增大而减小，可见，参数变异性对边坡稳定不利；当考虑区间时，失稳概率计算值接近于0，可靠性指标规律性不强，但均明显大于不考虑区间时的可靠性指标值，即考虑区间后对边坡稳定有利。

3.5 相关性的影响

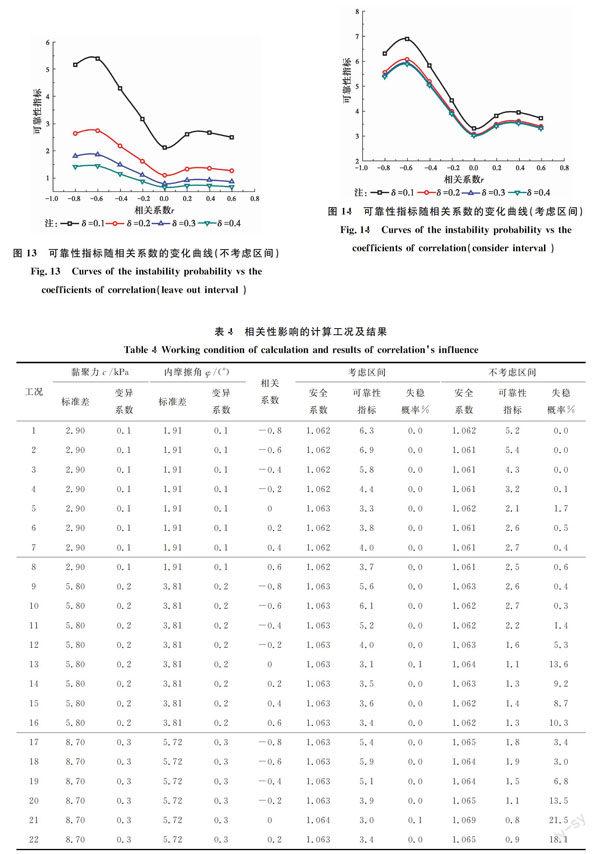
在参数c和φ均值和变异系数都不变的情况下，改变c和φ的相关系数进行边坡稳定可靠性概率分析，并分考虑区间和不考虑区间两种情况分别计算，计算工况及结果见表4，边坡的失稳概率和可靠性指标随c和φ的相关系数的变化曲线见图12、13和图14。

由于c和φ互相关的相关系数范围在-0.72～0.35之间[17]，由图可知，在各种变异系数情况下，当c和φ的相关系数为0时，边坡的失稳概率最大而可靠性指标最小，随着相关系数绝对值的增大，失稳概率逐渐变小而可靠性指标逐渐变大，且相关系数为负数时变化更加剧烈，可见，参数相关性对边坡稳定有利。从参数区间性来看，考虑区间时失稳概率计算值接近为0，而可靠性指标的变化规律更不考虑区间时类似，但数值上明显大于不考虑区间时的结果，进一步说明考虑区间后对边坡稳定有利。另外，从不同变异系数对应曲线的对比分析可进一步说明变异系数越大，边坡的失稳概率也越大。

从表4中计算结果可知，参数c和φ的相关系数对边坡稳定可靠度分析所得的安全系数影响很小。

4 结 论

以某高速公路全风化花岗岩土质高边坡为工程背景，在分析土质参数统计特性的基础上，利用极限平衡理论和蒙特卡罗模拟法，系统地分析了土质强度参数的均值不定性、变异性、相关性、区间特性和空间变化性等统计特性对边坡稳定可靠性的影响。

1）土性参数空间变化性对边坡稳定可靠性具有较大的影响，随着抽样距离的增加，可靠性指标总体趋势是下降的，一开始急剧下降，随后下降趋势变缓，最后趋于一个定值，正确认识和模拟空间变化性是正确采用可靠度计算边坡稳定性的前提。然而，目前抽样距离的计算尚无定论，建议在综合分析边坡潜在滑坡面的长度及所通过的土层的数目等因素确定。

2）强度参数c和φ的均值不定性、变异性和相关性对边坡稳定可靠性的均具有一定的影响，其中，φ的影响更加显著。可靠性指标随c或φ均值的增大而增加；失稳概率随c和φ的变异系数的增大而增大，可靠性指标随c和φ的变异系数的增大而减小，参数变异性对边坡稳定不利；当c和φ的相关系数为0时，边坡的失稳概率最大而可靠性指标最小，随着相关系数绝对值的增大，失稳概率逐渐变小而可靠性指标逐渐变大，且相关系数为负数时变化更剧烈，参数相关性对边坡稳定有利。

3）考虑参数区间性后，各组曲线的变化趋势大致不变，但是计算的失效概率明显小于不考虑区间时的结果，而可靠性指标明显大于不考虑区间时的结果，即考虑区间性的结果要趋于安全，对边坡稳定有利。

4）安全系数受强度参数均值的影响较大，而对参数的空间变化性、区间性、变异性和相关性均不敏感，由此可见，作为定值法的安全系数不能反应边坡稳定可靠性的情况。

5）准确而全面地考虑土质参数的统计特性，尤其是在参数变异性和相关性的基础上加以考虑土性参数空间变化性和区间性会更加符合工程实际，计算结果趋于安全，将有利于地基可靠度规范的制定和推广运用，有利于更科学合理地评价边坡工程的安全性。

参考文献：

[1]姚爱军， 薛延河. 复杂边坡稳定性评价方法与工程实践[M]. 北京： 科学出版社， 2008.

[2]Park H， Westb T R. Development of a probabilistic approach for rock wedge failure [J]. Engineering Geology， 2001， 59（3-4）： 233-251.

[3]朱红霞，闫澍旺.天津港地基土随机场特性及可靠度分析[J].岩石力学与工程学报，2007（Sup2）：3959-3965.

Zhu H X， Yan S W. Random field model and reliability analysis of foundation soil in tianjin port[J]. Chinese Journal of Rock Mechanics and Engineering， 2007（Sup2）： 3959-3965.（in Chinese）

[4]陈鹏，徐博侯.基于因素敏感性的边坡稳定可靠度分析[J].中国公路学报，2012（4）：42-48.

Chen P， Xu B H. Reliability analysis of slope stability based on factors sensitivity[J]. China Journal of Highway and Transport， 2012（4）： 42-48.（in Chinese）

[5]李宗坤，杨艳荣.土体强度参数统计特性对土石坝边坡可靠性的影响分析[J].中国农村水利水电，2011（8）：146-148.

Li Z K， Yang Y R. The effect of strength parameters on reliability index of soil slope stability[J]. China Rural Water and Hydropower， 2011（8）： 146-148.（in Chinese）

[6]李萍，王秉綱，李同录，等.陕西地区黄土路堑高边坡可靠度研究[J].中国公路学报，2009（6）：18-25.

Li P， Wang B G， Li T L， et al. Study of reliability for loess cutting high slopes in Shaanxi province[J]. China Journal of Highway and Transport， 2009（6）： 18-25.（in Chinese）

[7]蒋水华，李典庆.基于随机响应面法和Sarma法的边坡可靠度分析[J].铁道工程学报，2011（7）：21-27.

Jiang S H， Li D Q. Analysis of reliability of slope stability with stochastic response surface and sarma method method[J]. Journal of Railway Engineering Society， 2011（7）： 21-27.（in Chinese）

[8]谭晓慧，王建国，刘新荣，等.边坡稳定的有限元可靠度计算及敏感性分析[J].岩石力学与工程学报，2007（1）：115-122.

Tan X H， Wang J G， Liu X R， et al. Finite element reliability computation and sensitivity analysis of slope stability[J]. Chinese Journal of Rock Mechanics and Engineering， 2007（1）： 115-122.（in Chinese）

[9]郑敏洲，简文彬，吴茂明.花岗岩残积土边坡稳定性可靠度分析[J].岩石力学与工程学报，2005（Sup2）：5337-5340.

Zheng M Z， Jian W B， Wu M M. Reliability analysis of stability of granite residual soil slope[J]. Chinese Journal of Rock Mechanics and Engineering， 2005（Sup2）： 5337-5340.（in Chinese）

[10]陈群，唐岷，朱分清.强度参数的不确定性对土石坝坝坡失稳概率的影响[J].岩土工程学报，2008（11）：1594-1599.

Chen Q， Tang M， Zhu F Q. Influence of uncertainty of strength parameters on instability probability of Embankment dam slopes[J]. Chinese Journal of Geotechnical Engineering， 2008（11）： 1594-1599.（in Chinese）

[11]赵明华， 曾昭宇， 刘晓明， 等. 考虑轴向横向荷载共同作用的基桩可靠度[J]. 建筑科学与工程学报， 2005， 22（2）： 57-60.

Zhao M H， Zeng Z Y， Liu X M， et al. Reliability of pile foundation under vertical and lateral loads [J]. Journal of Architecture and Civil Engineering， 2005， 22（2）： 57-60.（in Chinese）

[12]李志纯， 朱道立. 随机动态交通网络可靠度分析与评价[J]. 交通运输工程学报， 2008， 8（1）： 106-112.

Li Z C， Zhu DL. Analysis and evaluation of reliability for stochastic and dynamic transport network [J]. Journal of Traffic and Transportation Engineering， 2008， 8（1）： 106-112.（in Chinese）

[13]阙云， 凌建明， 曾四平. 加筋土路堤内部稳定的可靠指标分析[J]. 交通运输工程学报， 2006， 6（3）： 37-41.

Que Y， Ling J M， Zeng S P. Reliability index analysis of internal stability of reinforced embankment [J]. Journal of Traffic and Transportation Engineering， 2006， 6（3）： 37-41.（in Chinese）

[14]桂勇，鄧通发，罗嗣海.基于蒙特卡罗边坡稳定二元体系的建立与应用[J].岩土力学，2014（7）：1979-1986.

GuiI Y， Deng T F， Luo S H. Establishment of slope stability dual index system based on Monte Carlo simulation and its application[J]. Rock and Soil Mechanics， 2014（7）： 1979-1986.（in Chinese）

[15]桂勇，邓通发，罗嗣海，等.考虑力学水文双重效应的生态边坡长期稳定性分析[J].公路，2014（4）：209-216.

Gui Y， Deng T F， Luo S H， et al. Study of long-term stability of ecological slope with double effect of mechanics and hydrology[J]. Highway， 2014（4）： 209-216.（in Chinese）

[16]Krahn J. Stability modeling with SLOPE/W 2007 version， fourth edition： An engineering methodology[R]. Alberta： Geo-slope International Ltd.， 2007.

[17]李亮， 张丙强. c、φ相关性对边坡整体稳定性的影响[J]. 铁道科学与工程学报， 2004， 1（1）： 62-68.

Li L， Zhang B Q. Influence of correlations of c and φ on slope stability [J]. Journal of Railway Science and Engineering， 2004， 1（1）： 62-68.（in Chinese）

（编辑 胡 玲）