基于贝叶斯统计的金融市场若干风险测度分析
2015-05-30李振翔
李振翔

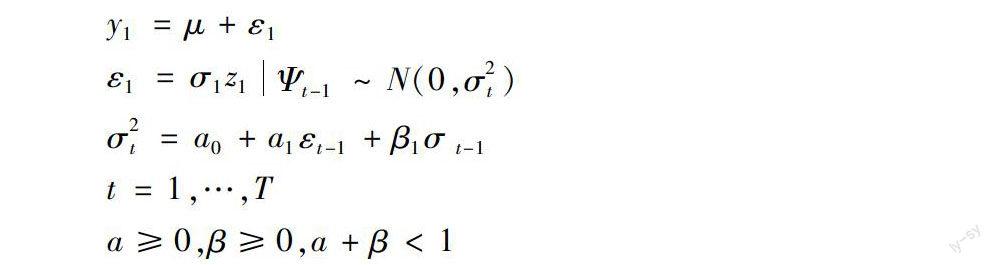
[摘 要]贝叶斯统计被很多人认为是唯一精确的统计方法,在各个领域都有所运用。随着我国对于经济发展的要求越来越高,金融市场更加繁荣,需求也有所提高。虽然我国目前金融市场运行良好,但是问题并不是突然出现的,往往在繁华的背后就会埋下风险的种子。本文基于贝叶斯的统计方法对金融市场的风险进行分析,使有关部门能够更加深入的了解金融市场运行,进行全程的把控,防止金融市场风险的演变,造成我国经济运行的混乱。
[关键词]贝叶斯统计;金融市场风险;测度分析
[DOI]10.13939/j.cnki.zgsc.2015.43.036
贝叶斯统计在桥梁设计、基因非编码区与模体识别、谷物的胚乳性状研究等多个方面都有所应用,是世界上最为先进的统计方法。金融市场包含多个方面,变量因素繁多,一直以来都没有建立一个能够全方位的进行风险测度的方法。原有的統计方法在现今金融结构中的运用已经跟不上市场发展的需求,这就要求我们必须建立一个可靠的、科学的统计方法,以便对金融市场的各方面进行监控。
1 贝叶斯统计的研究进展
对于贝叶斯统计与金融市场的结合不是短时间的,世界各国很早以前就开始对于这一方法进行系统的研究,希望能够把这一方法运用在金融市场中,增加市场的稳定运行。经济学家Zellner很早以前就提出了用贝叶斯的方法进行计量经济学中的分布滞后和完全递归模型的研究,得出了经济时间序列多维自回模型的预测分析。1965年Fama建立了随机游走模型,用来描述股价的变动,同时利用美国股票的价格证实了他的这一理论。在1983年Monahan利用贝叶斯的方法进行了模型识别、诊断检验等四项模型的分析期间只采用贝叶斯的方法。在1993年,West和Bauwens两人进行了动态角度的贝叶斯方法的使用,把贝叶斯的计量模型理论进行了完善。
在国内方面,我国也进行了大量贝叶斯模型的假设和研究,具有影响力的是王文玉在1981年以绝对损失函数为基础,使用贝叶斯的方法对一般形式的先验分布进行了预测,得出先验分布具有AR模型阶数和贝叶斯估计具有强一致性的结论。在1999年,吴长风等人利用GARCH模型对我国的股票市场的波动性方面进行了研究,得出波动性和收益率之间的关系。2007年,胡素华使用MCMC方法进行了连续时间随机波动的单一结构点与多变结构点进行了定位分析,实现了理论与实践方面的突破。2011年王汉赋等人利用贝叶斯风险对市场的风险资产损失进行了计量方面的研究,推导出了市场风险CVaR的计算公式。本文的所有理论技术和研究进程都是建立在前人研究的基础上的,再次感谢国际与国内学者的共同努力。
2 金融市场风险分析
所谓金融市场,就是资金的提供方与需求方使用一定的交易工具进行资金融通的市场,发展到现今阶段,构成形式非常的复杂,采用不同的划分方法往往就会分成完全不同的子市场。按照最简单融资时间长短的方法进行划分主要有融通时间在一年内的货币市场和融通时间超过一年的资本市场两方面。主要的交易工具有债券、股票、储蓄存单等。金融市场的主体包括金融机构、中央银行、工商企业、政府部门、家庭单位5个方面。各个方面与各个交易工具在不同子市场即兴交互,受到政策、经济形势、信用等多方面的影响就造成了金融市场的风险。其主要的表现形式是使资金经营者的实际收益与预期收益发生偏差,给资金经营者造成一定的损失或者是丧失收益[1]。
3 基于贝叶斯统计的金融市场若干风险测度分析
3.1 金融市场风险的主要因素
上文已经提到,金融市场的风险主要分为两个方面,即市场风险与信用风险。市场风险的影响因素主要有利率、汇率、股票价格和商品价格等,其发生风险的概率与市场成熟度成反比,只要市场的价格因素有所变动,就会发生市场风险,就会对金融机构造成损失,甚至是毁灭性的损失;在信用风险方面主要的风险因素是信用等级变化、信用价差波动和违约者三种信用造成的风险。其实,信用风险主要是一种违约风险,表现形式是金融机构的实际收益没有达到其目标收益而造成的损失可能性[2]。美国的次贷危机就是一个很好的例子。
3.2 市场风险的贝叶斯测度
金融市场风险无处不在,对其进行测度十分的必要,当代金融风险的度量是参照收益来进行的,以资本收益率的方法差或者是标准差作为风险度量的指标,其核心就是对收益率波动进行预测。结合上文中提到的研究成果,建立贝叶斯的GARCH-POT模型,使用两段分布模型进行测量,建立市场风险的测度模型如下:
y1=μ+ε1
ε1=σ1z1[JB(|]Ψt-1~N(0,σ2t)[JB)]
σ2t=a0+a1εt-1+β1σt-1
t=1,…,T
a≥0,β≥0,a+β<1
其中y是收益率;μ是条件均值;z是扰动项;ε是残差项;Ψ是以前各时刻的所有信息;σ是异方差。
以上模型的约束条件是针对贝叶斯统计设计的,这一方法无须考虑参数估计的二阶平稳性,可以对参数进行估计之后再利用贝叶斯的推断原理对平稳性进行判断和分析。但是上述模型不是完善的,这是因为二段分析中的GARCH模型具有杠杆效应,对于模型的数值会造成一定的影响,所以在上述的模型中加入
3.3 信用风险的贝叶斯测度
信用方面的贝叶斯模型主要是针对贷款来设定的,债务人如果违约或者是信用等级下降,就会给金融机构带来损失,金融机构进行的信用风险管理主要是在极值方面进行判断,以规避风险。根据上文中提到过的市场风险模型,进行度量风险的SW-GARCH-POT模型设定,进行债务人违约率与信用质量、连带效应与信用迁移,信用风险的SW-GARCH-POT模型如下:
yt=c(St)+εt
εt[JB(|]Ψt-1~N(0,σ2t)[JB)]
σ2t=μ(St)+ai(St)ε2t-i[DD(]p[]i=1[DD)]+βj(St)σ2t-j[DD(]q[]j+1[DD)]
其中S代表隐含变量。信用风险测度的SW-GARCH-POT模型扰动项的分布相对于市场风险的扰动项来说具有更厚的尾部特征,因此在尾部的高置区间分位数的确定依然用POT模型进行估计[4]。
4 结 论
贝叶斯模型的设计需要参考多种变量,本文针对金融市场的市场风险以及信用风险这两个主要风险进行了建模,可以利用这两种模型进行金融市场风险的测度。很多情况下,金融风险会不可避免地衍生成金融危机,需要我们早作准备。美国2008年的次贷危机已经有大型跨国金融机构进行了预测,但是由于市场结构等原因并没有引起足够的重视,也没有第一时间安排合理的措施。我国是社会主义国家,对于金融市场的宏观调控有着至关重要的作用,既然已经有了金融风险的测度模型,我们就要善加利用。
参考文献:
[1]王延彦.基于贝叶斯厚尾DCC-MSV模型的股市波动溢出效应研究[D].长沙:湖南大学,2014.
[2]汪青松.基于极值理论和贝叶斯估计的电力市场风险值VaR计算[D].重庆:重庆大学,2007.
[3]王正文.基于经济资本的中国财产保险业整合风险管理研究[D].武汉:武汉大学,2012.
[4]傅强,彭选华.基于MCMC算法的时变Copula-GARCH-t模型参数估计及应用[J].数量经济技术经济研究,2011(7):90-105,150.
