非完整统计概率分布的幂律化

李亚亚 胡娅娅

摘 要： 根据非完整统计的思想，利用最大熵原理，在约束条件下，推导了非广延参数相同和不同情况下正则系统和巨正则系统的统计分布，并借助Matlab绘制概率分布曲线。结果表明，当约束条件中非广延参数相同时，其概率分布为指数形式，这与Tsallis统计分布的幂律形式显然不一样；当约束条件中非广延参数不相同时，其概率分布不能精确求解，通过仿真拟合实现了幂律化。

关键词： 非完整统计； 统计力学； 仿真； 幂律化

中图分类号： O 414 文献标志码： A 文章编号： 1671-2153（2015）05-0094-03

1 提出问题

在复杂的物理系统中，如果不考虑系统内粒子之间的相互作用，就能够统计出可能出现的所有微观态的数目w，即有pi=1。如果考虑系统内粒子与粒子之间相互作用时，由于系统内相互作用的复杂性等因素的影响，导致无法准确统计可能出现的微观态的数目。设能够统计的微观态的数目为？淄，即有piq=1，把q称为非广延参数。其中？淄可能大于w，也可能小于w；当？淄=w时，所对应的统计为完整统计，当？淄≠w，所对应的统计为非完整统计，这是Q.A.Wang于2001年提出的非完整统计思想[1-2]，同时对统计力学中的shannon熵进行了变形，得出非完整shannon熵，即SqI=-kpiqlnpi，上标I代表非完整统计。在统计物理中，只要确定了所研究系统的概率分布函数，利用概率分布可得到统计系统的宏观性质。本文根据非完整统计思想，利用最大熵原理，推导了基于非完整shannon熵的正则分布（也称为E分布）和巨正则分布（也称N-E分布）。通过仿真，实现了统计分布的幂律化。

2 非完整shannon熵的E分布

若系统与源之间仅仅有热交换，这里忽略系统的粒子数涨落和体积涨落而认为各微观态的粒子数和体积取一定值N，V。由于热源很大，系统在源的作用下，各微观态的能量？着i可能不同，但在系统和源达到平衡时，系统的平均能量E是一定的，以Pi表示系统微观态的概率，取约束条件：

piq=1， （1）

piq？着i=E。 （2）

根据非完整统计思想，式（1）和式（2）可能具有不同的q值，这里假定它们相同的条件下，根据最大熵原理，所求的统计分布应使非完整shannon熵

SqI=-kpiqln pi， （3）

在约束下取极值，就可得到正则系统的统计分布。

引入Lagrange函数：

L=-+？酌（piq-1）+β（piq？着i-E）， （4）

求条件极值，=0得：

pi=e=， （5）

Zq（β，N，V）=e？酌=[exp（-βq？着i）]1/q ， （6）

其中：β，？酌为Lagrange乘子。因子e-？酌相当于归一化常数，当？酌=0，说明式（5）是归一化的。将式（5）和（6）分别称为E分布的概率分布函数和配分函数。

将式（5）带入式（3），并应用式（1）和式（2），可将式（3）化为

SqI=k[βE+lnZq（β，N，V）]， （7）

依据热力学基本关系：

N，V=kβ=， （8）

可得：

β=， （9）

则系统的平均热力学公式为

E=-lnZq（β，N，V）， （10）

式中：T为绝对温度；k玻尔兹曼常数。从式（9）中可以看出，β具有温度的性质，有时也称之为统计温度，很显然，当q=1时，就回到完整统计。

3 不同非广延参数下的E分布

由于系统内粒子相互作用的复杂性，根据非广延统计的思想，不论是约束条件，还是非完整shannon熵所对应的非广延参数可能不相同，由此将式（1）～式（3）改为

pia=1， （11）

pib？着i=E， （12）

SqI=-kpiclnpi， （13）

根据最大熵原理，应使式（13）在式（11）和式（12）的约束下取最大值。

引入Lagrange函数：

L'=piclnpi+？酌（pia-1）+β（pib？着i-E）， （14）

求条件极值，=0得：

lnpi=， （15）

式中：a，b，c为不等于零的实数。式（15）是不同非广延参数下E分布函数，由于a，b，c取值的变化性，要计算某一能量为？着i的微观态所对应的概率Pi，是非常困难的，只能借助计算机仿真模拟。

4 不同非广延参数下的N-E分布

如果系统与热源之间仅有粒子和热交换，且系统的各微观态的体积具有同一个固定值V时，此时所对应的系统为巨正则系统（或称N-E系统）。取系统限制条件：

piaNi=N， （16）

pib？着i=E， （17）

pic=1， （18）

Sq=-kpidln pi， （19）

引入Lagrange函数：

L=-+？酌（pic-1）+α（piaNi-N）+β（pib？着i-E），

（20）

式（20）中的α，β和γ为拉格朗日乘子。求？坠L/？坠pi，并令？坠L/？坠pi=0，得概率分布为

dpidlnpi+pid+αaNipia+βb？着ipib+？酌cpic=0。 （21）

式（21）也称为不同非广延参数下N-E分布，显然其概率分布非常复杂，只能借助计算机仿真模拟。

5 仿真模拟

由于不同非广延参数下E分布函数和不同非广延参数下N-E分布表达式非常复杂，通过仿真模拟来反映各量之间的函数关系。

在式（15）中，令pi=y，β？着i=x，为了保证？着i=E为常量时，有pibEi=E，即保证能量守恒规律的满足，令a=b，有

x=-？酌。 （22）

按照幂率形式利用Matlab软件进行拟合，任意取a=b=0.96，c=0.98，？酌=-10，便可得到拟合曲线（图略）。拟合方程为

y=-0.0039x5+0.2117x4-4.6422x3+51.2697x2-

285.6103x+643.2631，（23）

由式（23）可以看出，拟合方程实现了幂律化。

在式（21）中，令αNi=x，pi=y，β？着i=z，则

z=-yd-blny-yd-b-xya-b-？酌yc-b。 （24）

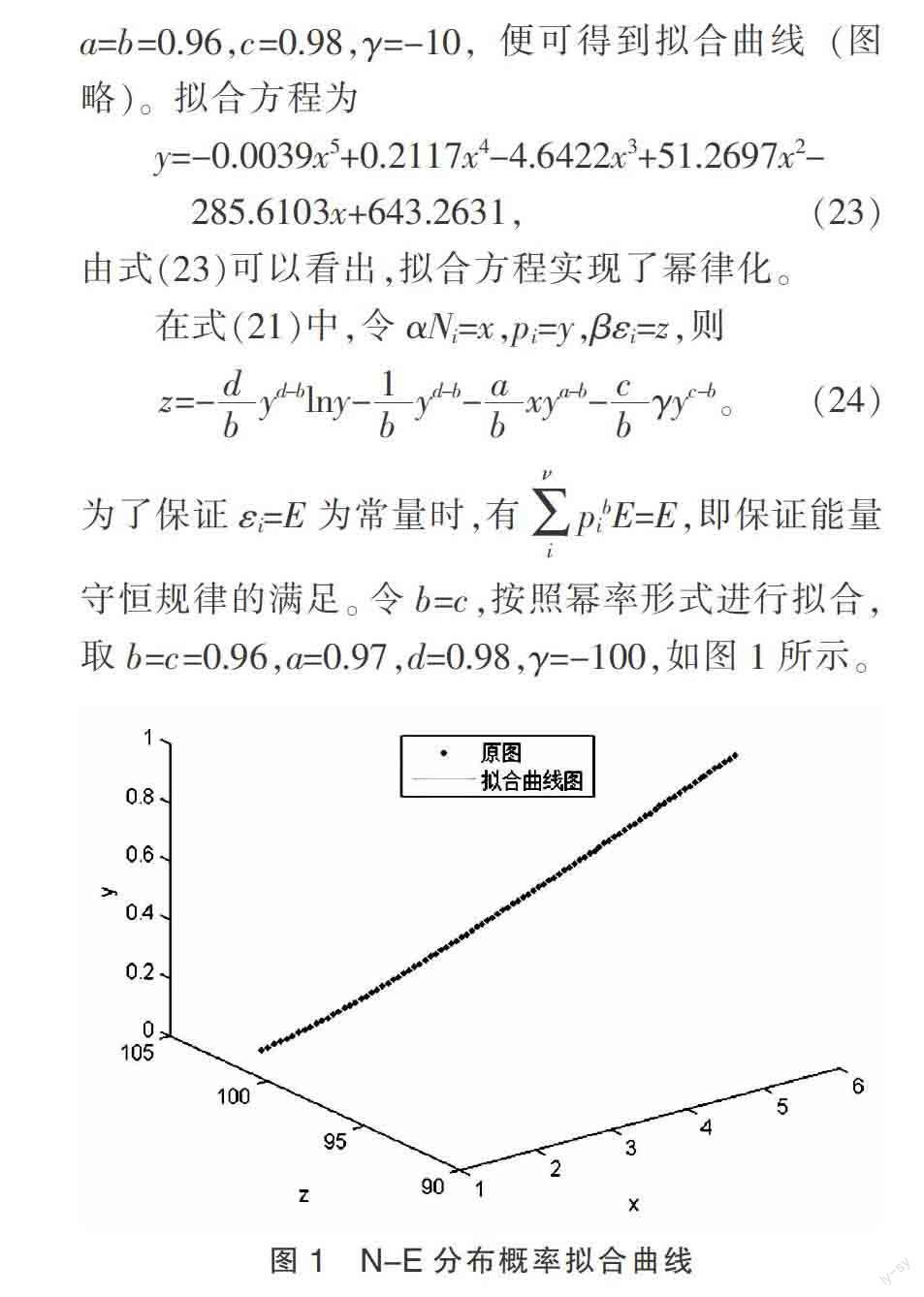
为了保证？着i=E为常量时，有pibE=E，即保证能量守恒规律的满足。令b=c，按照幂率形式进行拟合，取b=c=0.96，a=0.97，d=0.98，？酌=-100，如图1所示。

y=-0.6842+0.2032x0.9968+0.2233z0.2076， （25）

拟合之后，误差的平方和为1.8121×10-7，很好的实现了巨正则分布的幂律化。

在正则系统和巨正则系统中，由等概率假设和各态历经假设所得到的统计分布函数是指数形式[3]，而1988年巴西物理学家Tsallis设计了非广延的Tsallis熵，基于其推导出了Tsallis形式的幂律形式[4]。凝聚态物质中的分形行为[5]，反常扩散等须用幂律分布来解释；群集动物的社会行为和觅食行为也都表现出遵循幂律分布。在本文中，基于非完整shannon熵推导出非完整的正则分布（式（15））和巨正则分布（式（22））的函数形式非常复杂，通过计算机仿真模拟，实现了粒子之间相互作用复杂系统分布的幂律化，为研究一类遵循幂率分布的复杂系统提供了依据。但指数形式分布与幂律形式分布之间是否有联系？如果有，究竟是什么因素导致它们之间的这种联系，有待于深入探索。

参考文献：

[1] QIUPING A W. Incomplete statistics and nonextensive generalizations of statistical mechanics[J]. Chaos， Solitons and Fractals，2001，12：1431-1437.

[2] 李亚亚，胡娅娅. 非完整统计在完全开放系统中的概率分布[J]. 大理学院学报，2013，12（4）：34.

[3] 李鹤龄，宋金国，雷润洁. 非广延统计力学与完全开放系统的统计分布[J]. 大学物理，2010，29（5）：17-22.

[4] TSALLIS C. Possible generalization of Boltzmann-Gibbs statistics[J]. J. Stat. Phys.，1988，52（1-2）：479-487.

[5] RAFAEL M. Fernandes and Jorg Schmalian[J]. Phys. Rev. Lett.，2011，106：67004.