风扇的布局优化模型研究

吴晓林 朱倩倩 卢浩

摘 要：文章研究了在环境、空间、性能一定的情况下，将风扇放置于不同位置处，以达到布局最优的规划问题。布局最优由风扇的风速（风量）和噪音程度决定。首先，利用单摆法测量风力，再加上已知的物体重力，可以推算出风力的大小。其次，由风力计算风速：在选定的点处放置物体通过该物体的受力来估算该点的风速（事实上是周围若干点的集合，物体的受力并不均匀，但是微积分的工作量太大，我们决定不用这种太过专业的方法）。然后，根据风速的不同（即距离风扇位置的不同）测量相应的噪音程度，记录数据。最后，设定风扇的风速（风量）和噪音程度所占权重来考察距离风扇中心何种位置受益最大，即为风扇的最优布局。

关键词：风力；风速（风量）；噪音程度；权重

中图分类号：U412.1 文献标识码：A 文章编号：1006-8937（2015）26-0003-02

1 相关公式

在测量风速的过程中，单摆周期公式为：

g是重力加速度。造成重力加速度的原因是重力，那么当我们把风扇的风力加到某一物体上时，该物体做单摆运动时将有新的等效重力加速度和新的平衡位置。这时：

那么通过对T和T1的测量。

由风力计算风速时，我们用规则的圆柱体来做实验器材，已知其质量为m，半径为r，高度为h，密度分布均匀。（r和h相对于圆柱体到电风扇中心的距离d而言是极小的）空气密度为p时，假设风与圆柱的碰撞是完全弹性的，则

F=2pv2S，S=πr2

F是风力，v是风速，S是圆柱体底面积，于是我们就可以求出v的大小（风量=风速×圆柱体底面积）。

2 重述问题

随着社会经济的不断发展，市场上风扇的销售数量大不如前，大多数消费者更倾向于选择空调来缓解炎热，但这并不意味着风扇一无是处，反而我们更要提倡人们尽可能的使用风扇。由于国家资源日渐短缺，可持续性发展道路是我们最终的目标。根据市场调查发现，近几年电风扇的销售量正在大幅度的增长，我们完全有必要对风扇利用进行深入的研究。又因为人们对风扇布局最优的概念比较浅薄，而市场主要着重对风扇外观的设计以达到盈利的目的，因此我们着重通过对风扇布局的研究使风扇利用最大化，改善空气，减少资源的消耗。

研究风扇布局最优的问题，我们主要通过对距离风扇不同位置处风速（风量）和噪音程度的研究来确定风扇布局最优处。我们的工作是：①如何测定风速（风量）；②如何测量噪音程度；③如何设定综合指标考察距离风扇中心何种位置受益最大。

3 问题分析

3.1 测量风速（风量）

先测量风力：最开始考虑实验方案的时候我们想了许多静力学方面的方案，但是由于静力场测量时风的不稳定造成了测量的不准确度大大增加，于是我们决定另辟蹊径，利用单摆法。单摆周期公式为：

g是重力加速度，造成重力加速度的原因是重力，那么当我们把风扇的风力加到某一物体上时，该物体做单摆运动时将有新的等效重力加速度和新的平衡位置。这时：

那么通过对T和T1的测量，再加上已知的物体重力，可以推算出风力F的大小。然后计算风速：在选定的点处放置物体通过该物体的受力来估算该点的风速（事实上是周围若干点的集合，物体的受力并不均匀，但是微积分的工作量太大，我们决定不用这种太过专业的方法）。

我们用规则的圆柱体来做实验器材，已知其质量为m，半径为r，高度为h，密度分布均匀。（r和h相对于圆柱体到电风扇中心的距离d而言是极小的）空气密度为p时，假设风与圆柱的碰撞是完全弹性的，则

F=2pv2S，S=πr2

F是风力，v是风速，S是圆柱体底面积，于是我们就可以求出v的大小（风量=风速×圆柱体底面积）。

3.2 测量噪音程度

3.2.1 噪声标准

0 dB的标准设定，是根据听力正常的人所能听到的最小的声音而厘定的。每增加10 dB等于强度增为10倍，增加20 dB增为100倍，30 dB则增为1 000倍。

0 dB：勉强可听见的声音，如微风吹动的树叶声；20 dB：如低微的呢喃；40 dB：如钟摆的声音。

3.2.2 测量方法

①准备好试验仪器、记录表以及相应的测试架和导管；②检查试验仪器、样机状态是否符合试验要求；③测试架四脚须平稳，不得有晃动或振动声出现；④将所要测试的产品需按模拟正常使用方式安装固定在隔音室测试架上，确保换气扇与地面垂直距离至少为1.3 m，关上隔音室的内、外隔音门，并且先给其通电运行不少于5 min后对其进行测试；⑤测试时将噪音计的麦克风头正对被测试样机的指定位置，等数据跳动达到稳定状态时，记录各点测试数据，最终取各数据的平均值为准。

4 符号说明

各种符号的含义，见表1。

5 模型假设

假设风扇较新，无不良因素影响；假设风扇不受外来环境的影响；忽略周围环境对风扇噪音产生的影响。

6 模型建立

根据市场调查，人们对风速的需求远大于对噪音的抵触，本文仅设定权重比为8∶2，即最优值=风速值*80%-噪音值%20%。

7 模型求解

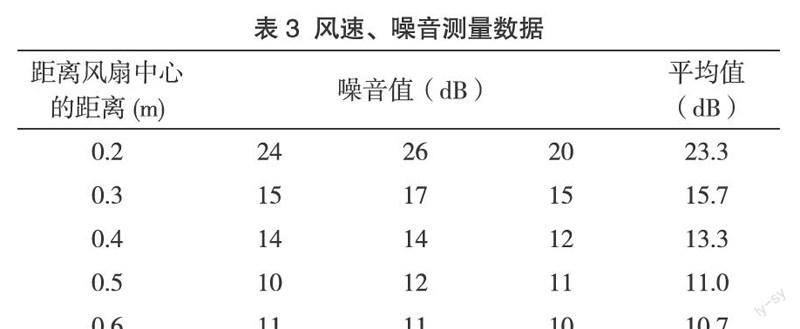
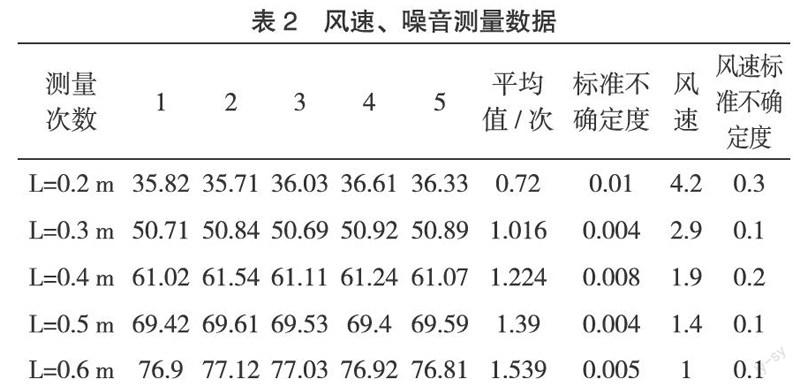
7.1 风速、噪音测量数据

风速、噪音测量数据，见表2、表3。

由以上数据可分析得到，在实际生活中人们安装风扇的位置不宜过近或过远，要充分考虑众多方面的因素。

当设定的权重不同时，最优解不同，本文仅建立在市场调查的基础之上，因此人们可以根据自身偏好重新选取权重比，达到理想的最优布局。

8 模型评价

8.1 模型的优点

①影响风扇布局的因素繁多，本文化大为小，选取仅决定性因素。

②由于测量的数据并不能直接体现风扇的布局最优问题，本文借助于权重，简洁明了。

8.2 模型的缺点

①决定风扇布局的因素还有很多，本文仅考虑了风速和噪音，考察不够全面

②距离的选取过于片面，不能充分体现不同位置处风扇的性能；

③权重比的选定说明不充分。

参考文献：

[1] 段家忯.新编基础物理实验[M].北京：高等教育出版社，2006.

[2] 高会生.MATLAB原理与工程应用[M].北京：电子工程出版社，2006，（10）.