预应力混凝土连续梁桥施工监控

娄锋

摘 要：本文背景桥梁为40+60+40m的三跨预应力混凝土连续箱梁，其施工方案为挂篮悬臂浇筑。本文主要研究桥梁的施工监控全过程。同时由于本桥宽跨比较大，剪力滞效应明显，本文将通过对比，研究剪力滞效应对本桥的影响。

关键词：预应力混凝土连续梁；挂篮悬臂浇筑；施工监控；剪力滞效应

1 基本概况

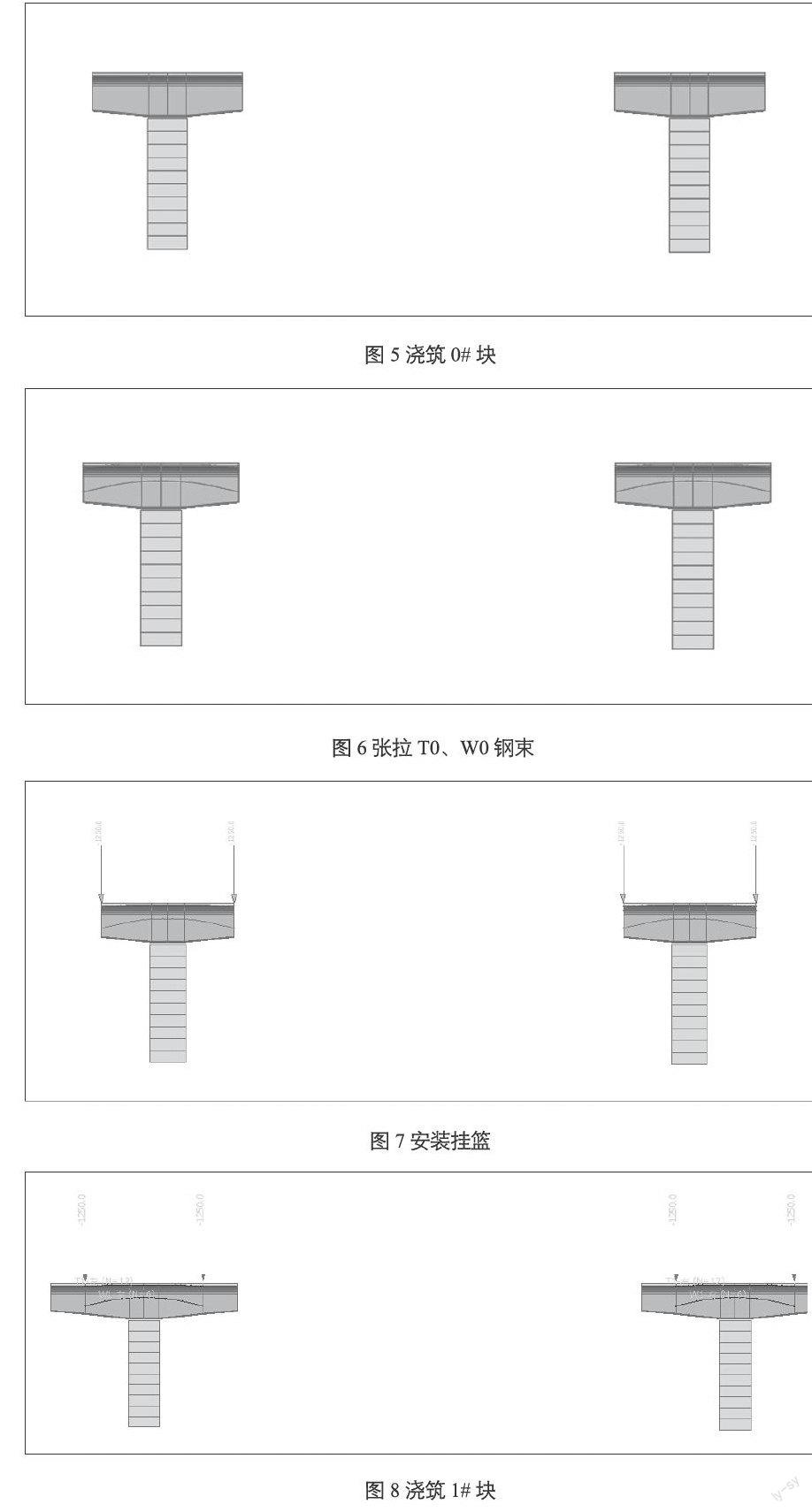
背景桥梁为左幅为40+60+40m的三跨预应力混凝土连续箱梁，上部结构为全预应力构件，采用单箱五室变截面，顶板宽33m，墩顶梁高3.8米，跨中梁高2.0m，按照1.6次抛物线变化。边跨10m范围内为等截面，梁高2.0m。施工方案为挂篮悬臂浇筑。其桥型布置图、箱梁截面及施工阶段划分见下图：

2 计算模型

本文采用有限元软件MIDAS/CIVIL建立杆系单元模型，模拟桥梁的整个施工过程。模型共有46个主梁单元，20个桥墩单元，共计66个单元。结构计算模型参见下图：

2.1 主梁结构受力分析

分别对主梁结构施工阶段抗弯承载能力、运营阶段抗弯承载能力、抗剪承载能力、抗裂性、正截面压应力及挠度进行验算，结果表明，上述各项均满足规范要求，说明主梁结构设计合理，能够满足设计荷载即公路-Ⅰ级正常运营。

2.2 桥梁施工监控

施工监控的主要内容包括变形及线形监控、应力监控。

2.2.1变形监控

变形测点布置于各节段端部0.5m处，每断面布置2个测点（左、右两侧），横断面测点布置图如下：

成桥后，在每个节段的中央分隔带边缘和防撞护栏边缘各设置一个标高测点，每个截面共4个测点，测点布置如下图所示。

由于背景桥梁为40m+60m+40m的预应力混凝土连续梁桥，其几何非线性表现不明显，故而在确定正装分析法初始线形状态时，无需迭代，直接可由倒装分析法确定。

本桥的理想设计状态为成桥10年后桥梁可维持半个活荷载挠度的上拱度，以确保桥梁的正常使用，同时保持优美线形。由此可推知成桥阶段桥梁的理想线形，详見下图。图中，Y1（x）表示1/2活荷载长期挠度的上拱度；Y2（x）表示成桥10年内恒荷载作用的长期挠度的上拱度，令Y0（x）=Y1（x）+ Y2（x），通常称为预拱度，此曲线计算后须拟合为顺滑曲线。

以上述成桥状态结构的理想状态作为倒装分析的初始状态进行倒拆，可推出正装分析的初始状态，即为桥梁施工时各节段的浇筑后标高。

各节段在施工过程中将产生以下变形：

（1）节段浇筑时挂篮受混凝土湿重作用产生的弹性变形Y3（x）；

（2）模板在混凝土湿重作用产生的弹性变形Y4（x）；

（3）当前节段在后续施工过程中预应力、临时施工荷载以及其它恒荷载等作用下产生的变形Y5（x）；

为此，采用叠加原理，可知桥梁施工过程中各节段的立模标高由下式计算：

各节段立模标高=设计标高+ 预抬值+修正值；

预抬值=Y1（x）+ Y2（x）-Y3（x）-Y4（x）-Y5（x）。

本文施工监控采用预测控制法和自适应控制法相结合的方法，在施工过程中，通过上式对后续节段立模标高进行预测，同时对当前施工节段变形进行跟踪观测，如有误差超限，则通过对后续施工节段实时修正来予以消除。

另外，由于本桥边跨9m范围采用布设支架整体现浇，其预抬值计算用下式计算：

预抬值=Y1（x）+ Y2（x）-Y5（x）+ Y6（x）；

其中Y6（x）为支架变形，其值由支架预压试验确定。

据此，计算得各节段施工预抬值Y0（x）线形及成桥理论线形如下图所示：

根据上述方法，各施工阶段结束后及成桥阶段实测标高与上述理论标高比较吻合，最大相对误差控制在2cm以内，说明立模精度得到很好的控制。

2.2.2应力监控

截面顶（底）板实测应力为截面顶（底）板上各测点应力的平均值，理论应力为按照有限元程序MIDAS/CIVIL建立杆系单元模型计算的截面顶（底）板应力值。

本桥共设12个截面对施工过程中主梁应力发展进行跟踪观测，并实时与理论设计值进行对比，对比发现：主梁应力监测截面的实测应力值及其变化趋势与理论计算结果比较吻合，但二者也存在一定的偏差。

受篇幅所限，本文仅列出主梁在1#墩中跨侧悬臂根部截面（即截面4）的施工各阶段应力数据：

2.2.3剪力滞效应研究

为计算考虑剪力滞效应的理论应力值，本文采用梁格法建立MIDAS/CIVIL空间杆系单元模型，将其计算结果与前文中按照初等梁理论建立的二维杆系模型进行对比，以计算其剪力滞效应。梁格法建立的空间杆系单元模型见下图：

结合背景桥梁的实际情况，拟选取最大悬臂施工阶段中跨0#块截面、L/4截面（即截面4、5、6）及成桥后跨中截面共3个截面作为研究剪力滞效应的观测截面。

由图 25可知，最大悬臂阶段，0#块截面剪力滞效应明显，在横向上不同腹板处剪力滞系数不等，正负剪力滞同时出现，最大正剪力滞系数1.21，最小负剪力滞系数0.80：

由图 26可知，最大悬臂状态L/4截面剪力滞效应分析结果，最大悬臂阶段，L/4截面剪力滞效应明显，在横向上不同腹板处剪力滞系数不等，正负剪力滞同时出现，最大正剪力滞系数1.31，最小负剪力滞系数0.90：

由图27可知成桥阶段跨中截面剪力滞效应分析结果，成桥阶段，跨中截面剪力滞效应明显，在横向上不同腹板处剪力滞系数不等，正负剪力滞同时出现，最大正剪力滞系数1.15，最小负剪力滞系数0.72：

3 结语

本文以一座预应力混凝土连续箱梁桥为背景，进行其施工阶段的分析控制研究。并结合其宽桥特征，对其剪力滞效应的影响进行了初步分析。本文主要结论如下：

主梁结构施工阶段抗弯承载能力、运营阶段抗弯承载能力、抗剪承载能力、抗裂性、正截面压应力及挠度验算，均满足规范要求；各施工阶段结束后及成桥阶段实测标高与上述理论标高比较吻合，最大相对误差控制在2cm以内，说明立模精度得到很好的控制；主梁应力监测截面的实测应力值及其变化趋势与理论计算结果比较吻合，但二者也存在一定的偏差。

参考文献：

[1] 杨允表，黄剑源.钱塘江二桥变截面连续箱形梁剪滞效应的分析[J].宁波大学学报： 理工版.1992（02）：83-92.

[2] 郭金琼，房贞政，罗孝登.箱形梁桥剪滞效应分析[J].土木工程学报.1983（01）：1-13.