三坐标测量涡轮导向叶片排气面积的方法研究

中航工业沈阳发动机设计研究所 高继昆

涡轮导向叶片排气面积，反映了其流通能力。对于发动机而言，涡轮叶片排气面积对涡轮前后温度、流量、推力等性能都有直接的影响，能够显著影响整机性能，是备受总体关注的参数。要有效地控制涡轮叶片排气面积，需要进行准确的测量。导向器叶片本身是一个扭曲的空间型面，它使喉道排气面积成为一个不规则截面，这对真实测量面积大小带来很大困难。因此，国、内外都规定在某一个位置上测量一个当量面积来代替真实面积。排气面积几何测量通常分为测具测量和坐标测量。测具测量往往用于批产阶段，对于大批量的相同叶片使用一个较为固定的测具进行排气面积测量能够大大节省成本和工作时间。目前在国内外发动机主要生产厂家大都采用这种测量手段。而在科研阶段，技术状态不固定，叶片结构存在更改的可能，这种情况下测具测量则比较浪费。坐标测量则凭借较高的精确度和测量能力成为了该阶段较为有效的方法之一，更可以作为一种计量手段，评定测具测量的准确性。

本文应用三坐标测量机测量涡轮叶片排气面积，进行排气面积坐标测量方法的试验研究。在测量过程中，采用不同的坐标测量方法得出排气面积值。通过对排气面积数值的对比分析，研究不同测量方法的精确度。

1 测量方法

1.1 流道检测点检测

为验证坐标系的重复性，应对流道测点的Z0坐标进行测量，通过对长度的直接测量，得到坐标系长度测量的重复性差异，作为后续测量的参考数据。

根据检测要求确定流道检测点的位置，得到流道检测点在涡轮叶片坐标系下的名义点坐标。如果已给出流道检测点的名义法线，可直接按法线方向测量得到流道检测点的实测值。如果未给出流道检测点的名义法线，则用微小平面法测量得到名义法线方向，再按该法线方向测量得到流道检测点的实测值。

1.2 排气面积检测

可采用触测法和扫描型线法进行检测。其中，触测法为当前常用的检测方法，该方法较为便捷，但是其取点方式因矢量方向的不同会引入一定测量误差；而扫描型线法从其物理意义来说更加接近所需的真实值，但其效率决定了该方法不能适应工程化测量，仅能作为计量手段使用。

1.2.1 触测法检测

根据检测要求确定喉道宽度检测点和高度检测点的位置，得到喉道宽度检测点和高度检测点在叶身坐标系下的名义点坐标。得到检测点的实测值。

1.2.2 扫描型线法检测

根据检测要求确定并扫描各高度叶片叶盆、叶背侧形成最小喉道宽度的一段型线和通过高度检测点的缘板型线，得到各型线的实际点坐标。叶盆和叶背扫描段点间距不大于0.5mm，叶缘扫描段点间距不大于0.1mm，设定时应根据扫描段的曲率变化适当缩小点间距值。

2 测量步骤

2.1 零件的装夹

涡轮叶片的装夹应按照装夹可靠、建立测量坐标系方便、不妨碍测量、有足够的检测空间的原则进行。优先选用专用夹具，无专用夹具时也可选用通用夹具。

2.2 导入数据模型

数据模型应保证完整准确，叶身光顺，无冗余、无碎面，叶缘良好，工件坐标系准确并与设计基准一致。导入数据模型，并将数据模型实体化显示。

2.3 测针配置

根据零件结构的特点选择合适的加长杆和测针。涡轮叶片的检测点和扫描型线的方向和角度不同，需配置多角度测针。测量过程中使用的所有测针或所有测针角度均需经过统一校准。

测针角度应根据涡轮叶片检测点和扫描型线的位置情况设置，确保在测量过程中，测头与零件不发生干涉。

测针配置的原则是：选用测针的直径尽可能小、加长杆尽可能短、连接点的数目尽可能少、配置最少的测针或测针角度完成所有检测任务。

2.4 建立叶片坐标系

采用6个矢量点迭代的方法建立涡轮叶片坐标系，矢量点应选取在精度较高的机加工表面上。矢量点和收敛误差应按照检测要求选取确定，如没有具体要求，可自行选取确定。

以某型号发动机涡轮叶片为例，如图1所示。根据轴向基准点1、2、3三点、径向基准点4、5两点以及周向基准点6、7的中点，进行迭代。首先选择6点迭代模式建立坐标系并输入收敛误差，然后按顺序手动测量迭代点，点的位置在名义点的位置附近即可，最后自动运行进行循环迭代。当迭代前后差异小于所设定的收敛误差时迭代停止，认为确定了该涡轮叶片的坐标系。在叶片坐标系下完成流道检测点的检测。

2.5 建立叶身坐标系

根据检测要求和图纸确定被测窗口的叶身坐标系与涡轮叶片坐标系的关系，通过平移旋转得到叶身坐标系。在叶身坐标系下完成对应窗口排气面积的检测。

3 数据处理

3.1 选用评定方法

检测点和扫描型线通常都选用最小二乘法进行拟合。不包括叶缘部分的叶身扫描型线和上下缘板扫描型线在测量软件中直接进行拟合。包括叶缘部分的叶身扫描型线应利用Blade等专业叶型处理软件进行拟合。

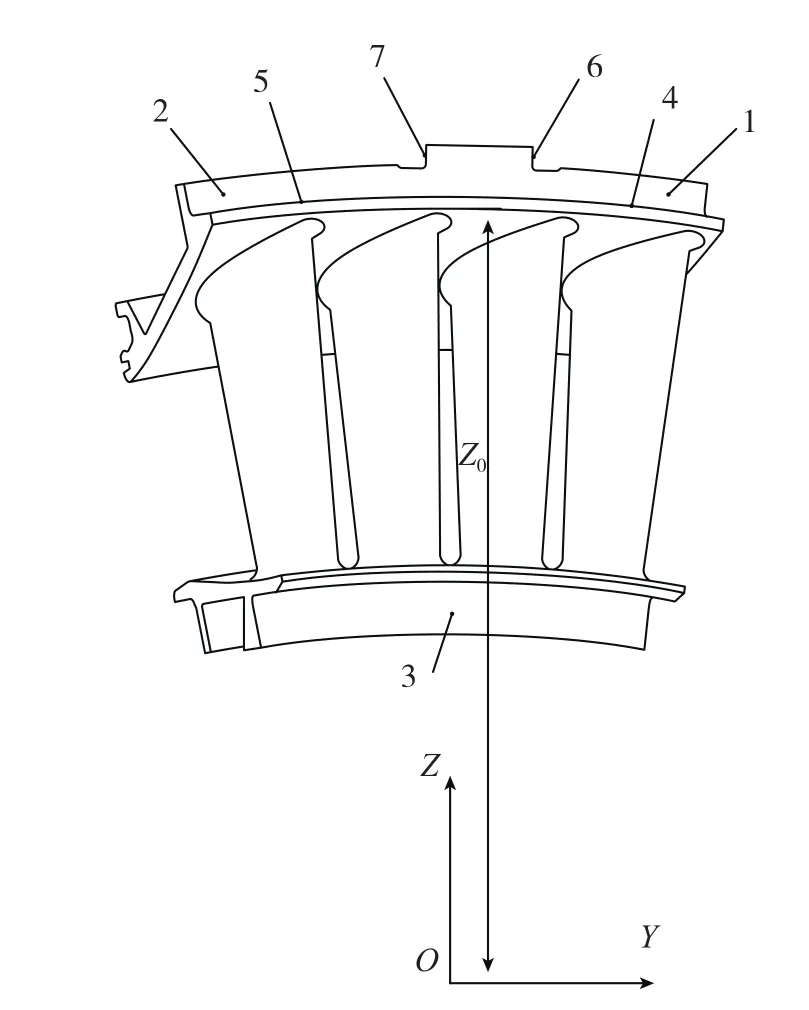
图1 用于确定涡轮叶片坐标系的定位点Fig.1 Orientation points to determine turbine guide vane coordinate system

3.2 计算排气面积

如采用触测法检测，在测量软件中可直接利用已测得的实际点坐标计算各截面的喉道宽度和通道的高度。

如采用扫描型线法检测，首先在测量软件中计算出各截面两条型线间的最小距离，如测量软件无法计算，可把测得的实际型线点坐标导入到其他三维软件中计算出各截面两条型线间的最小距离，从而得到各截面的喉道宽度。同时选取上下缘板扫描型线与相对应的理论轴向平面的两个交点，计算两个交点之间的距离得到通道高度。

根据公式下列公式可计算得到单个通道的排气面积。

式中：F为涡轮叶片单个通道的当量排气面积，单位：cm2；W1，W2，…，Wn为各截面的喉道宽度，单位：mm；H为通道的高度，单位：mm；K为修正系数。

3.3 测量数据对比分析

以某型号发动机涡轮叶片为例，对测量数据进行对比分析。

3.3.1 流道测点Z0坐标测量数据对比分析

按1.1中要求，进行迭代坐标系下的流道测点G3～G16的Z0坐标测量，通过数据对比，在一定程度上能够评价坐标测量方法的直接测量误差水平。以微小平面法确定实测点的法线和以名义点理论法线代替实测点的法线两种方法进行测量，得到实际点的Z0值，两种测量方法的差异最大值为0.004mm，见表1。

上述数据能够用于评估两种矢量方法获得的流道测量数据的差异水平。

3.3.2 测点矢量方向差异对排气面积的影响

在测量排气面积时，分别运用了微平面法和理论矢量法两种方法，获得的数据如表2所示。对比表明测量差异最大值为0.0027mm，出现在截面W3长度测量中。排气面积测量结果的差异值为0.001 cm2。

表1 两种矢量选取方法测量Z0坐标的数据差异

3.3.3 触测法和扫描型线法测量数据对比分析

在测量排气面积时，分别运用了触测法和扫描型线法两种方法，获得的数据如表2所示。对比表明测量差异最大值为0.0221mm，出现在截面W3长度测量中。排气面积测量结果的差异值为0.011 cm2，排气面积测量结果的相对差异值为0.1%。

表2 不同方法测量排气面积的数据差异

3.3.4 测量数据对比分析结果

（1）对同一组涡轮导向叶片组件同一个完整窗口进行排气面积测量，触测法和扫描法的数据差异范围最大为理论值的0.11%。满足国军标中对测量不确定度的要求（允差的1/4）。

（2）测量结果均表明，扫描法测量排气面积获得的结果比触测法小0.1%。

（3）在应用触测法测量排气面积时，理论矢量法与微平面法测量差异不大。

（4）定位基准的选择对测量结果有影响，基准的选择对坐标系的确定有影响，进而影响了测量结果。

4 不确定度分析

排气面积测量可采用触测法和扫描型线法两种方法进行测量，下面以扫描型线法为例对排气面积测量不确定度进行评定。

排气面积测量不确定度的主要来源有：三坐标测量机示值误差、扫描误差、半径补偿误差、测量重复性。

4.1 不确定度来源

使用三坐标测量机测量扫描叶片型线时，不确定度来源有：

（1）测量机示值误差引起的不确定度分量

（2）测量机扫描误差引起的不确定度分量

（3）测量重复性引起的不确定度分量

（4）半径补偿误差引起的不确定度分量

4.2 标准不确定度评定

4.2.1 测量机示值误差引起的不确定度分量u1

由校准证书可知，三坐标测量机示值误差不超过（1.5+L/350）μm，在该叶片型线测量中取L=200mm，则a=（1.5+200/350）/2=1.0μm，为矩形分布[1-2]，b＝0.6，则

4.2.2 测量机扫描误差引起的不确定度分量u2

由校准证书可知，扫描误差不超过1.3μm，则a＝0.65μm，估计为矩形分布，b＝0.6，则

4.2.3 测量重复性引起的不确定度分量u3

在重复性条件下，对同一叶片同一截面叶型进行十次重复性测量，每一次测量后计算其轮廓度误差x，得到测量结果：

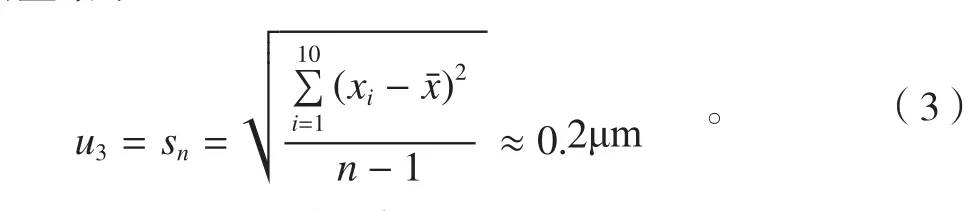
4.2.4 半径补偿误差引起的不确定度分量u4

三坐标测量机的半径补偿误差也称余弦误差，产生的原因是半径补偿的方向与实际触测点的法线方向不一致引起的。

半径补偿误差可以由以下公式计算得到：

式中，R=1mm为测针半径；β＝10°为测量点实际法线方向与半径补偿方向偏差，即实际点法线方向与XY平面的夹角；H=0.05mm为实测点Z值偏差。

估计为矩形分布，a＝δ＝6.6μm，b＝0.6 ，则

4.2.5 合成标准不确定度

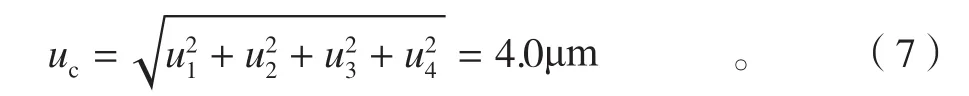
4.2.6 扩展不确定度

取置信概率p=95%，k=2，则扩展不确定度：

经过计算其扩展不确定度能够满足现阶段涡轮导向叶片排气面积测量公差的检测技术要求。

5 结论

涡轮导向叶片排气面积测量，在原有测具测量的基础上，采用三坐标测量机结合精密气动转台进行排气面积检测。利用迭代法建立坐标系，采用触测法或扫描型线法进行测量，应用三坐标测量分析软件的各项功能，计算出排气面积，是国内测量涡轮导向叶片排气面积比较先进有效的方法。

[1] 倪育才. 几何量测量不确定度评定.北京：中国计量出版社，2006.

[2] 宣安东. 实用测量不确定度评定及案例.北京：中国计量出版社，2007.