基于单周期控制的双Buck逆变器数字化控制研究

陈勋，林琼斌，2，3

(1.福州大学电气工程与自动化学院，福建 福州 350108;2.浙江大学电气工程博士后流动站，浙江 杭州 310000;3.漳州科华电子博士后工作站，福建 漳州 363000)

1 引言

对于逆变器的研究，实现高效率和提高它的开关频率是逆变器的重要研究内容。在许多情况下，高效率和高开关频率是互相矛盾的，很难同时优化。传统桥式逆变器的续流是通过体二极管来续流，而体二极管的性能较差，同时反向恢复时间长，这将导致很大损耗并限制了开关频率的提高。而双BUCK逆变电路的续流二极管不是开关管的体二极管，而是单独的一个二极管，这样可以使开关管和二极管分别优化设计。同时双Buck逆变器拓扑能够克服传统桥式逆变器的开关管直通问题［1］。

本文基于双Buck逆变器拓扑，对其数字化控制方式进行研究。与模拟控制不同的是，数字控制具有硬件电路简单，抗干扰能力强，升级换代容易等优点，同时数字控制技术也是电源技术发展的必然趋势。通常的双Buck逆变器控制算法有基本PID控制、滞环电流控制、斜坡比较控制等。其中基本PID控制以其控制简单、参数容易整定等优点被广泛应用，但是单纯的PID控制对于较为复杂的控制系统会难以胜任，所以经常和其他的一些控制方法相结合。滞环电流控制是一种很好的非线性控制方法，实现电路简单，稳定性好，动态响应快，同时具有电流限制的能力，但是这种控制的开关频率是不断变化的，会导致滤波器难以进行选取［2］。斜坡比较控制是一种恒频的线性控制，通过设置三角载波的频率，时其与调制波进行交截，能够很方便的控制开关管，但是这种控制需要额外加入最小偏置电流，造成滤波电感中始终有环流通过，导致逆变器效率难以提高。基于上述控制方法的优缺点，本文将采用双环控制，内环基于单周期控制的电流控制算法，外环基于PI控制的方法对双Buck逆变器拓扑进行数字化控制。单周期电流控制是数字控制特有的一种控制算法，这种控制算法能根据逆变器当前时刻的状态方程和输出电感电流反馈信号来计算当前开关周期的占空比，对系统参数变动反应灵敏，具有较好的稳态输出特性。同时外环采用PI控制对采样电压与给定电压的误差进行控制，使输出电压的幅值与给定电压较为稳定地变换。通过这两种控制相结合的双环控制，能够很好的结合两者的优点，克服两者的缺点，使输出电压波形与给定电压很好地进行跟踪，输出电压波形质量更好，同时满足较低的输出电压波形畸变率。

2 电感电流单周期控制算法

双Buck逆变器拓扑工作时可分为四个工作模态，如图1所示。(其中L1=L2=L)

模态1:开关管S1导通，S2关断时(等效电路如图1中模态1所示)，流过电感L1的电流线性增加，它的变化率为:

在此模态中，电感电流大小以(Ud－Uo)/L的斜率上升，此时的续流二极管是不导通。

模态2:开关管S1导通和S2都关断时(等效电路如图1中模态2所示)，此时续流二极管D1导通，流过电感L1的电流线性下降，它的变化率为:

在此模态中，电感电流大小(－Ud－Uo)/L的斜率下降，续流二极管D1导通。

模态3:开关管S1关断，S2导通时(等效电路如图1中模态3所示)，流过电感L2的电流线性增加，它的变化率为:

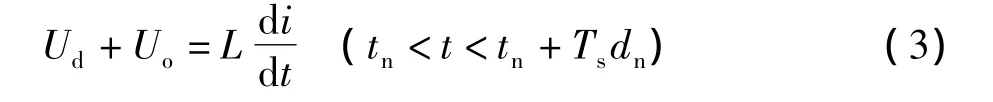
在此模态中，电感电流大小(Ud+Uo)/L以的斜率上升，此时的续流二极管D2不导通。

模态4:开关管S1和S2都关断时(等效电路如图1中模态4所示)，流过电感L2的电流线性减小，它的变化率为:

在此模态中，电感电流大小以(Uo－Ud)/L的斜率下降，此时续流二极管D2导通。

下面对每个开关周期的占空比公式进行推导，先对输出正半周的模态1和模态2进行分析，可得如下关系式:

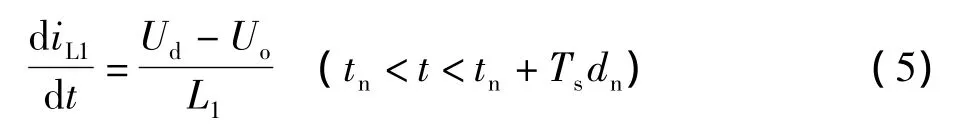
即

图1 四种电路工作模态

可得电感电流iL1在第k个开关周期的S1导通期间内上升电流为:

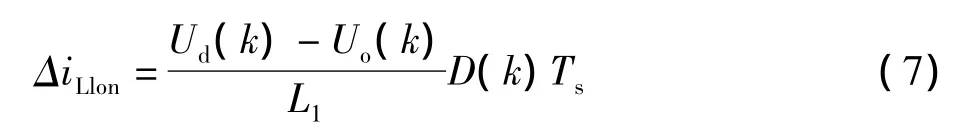
这是先由模态1所得，接下来根据模态2可得:

即

可得电感电流iL1在第k个开关周期的S1关断期间内下降电流为:

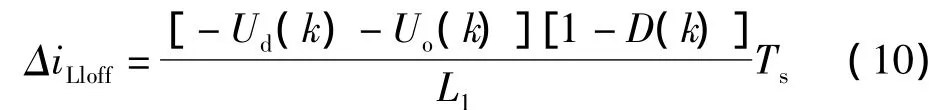
综上可得第k个开关周期的电感电流变化量为:

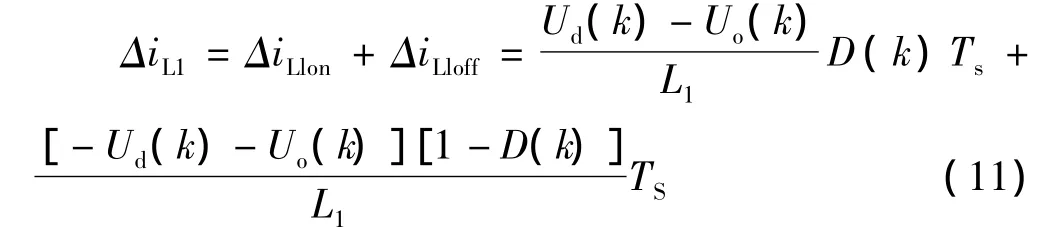
由上式可得占空比为:

3 控制系统设计

本文的控制方式是基于外环PI内环单周期控制，同时内环单周期控制还具有预测电流的效果，能够使电感电流很好地跟踪下一拍预测的给定电流。基本控制系统框图如图2所示。

图2 双Buck拓扑控制系统框图

电流内环控制的原理是基于单周期控制的思想，单周期控制能够根据当前开关频率、当前输出电压、输入电压和电感电流实时控制，每个开关周期的占空比的值都达到最佳，并且使被控对象的输出信号在每个开关周期内的平均值等于参考值，在当前的开关周期内能够消除此时的瞬态误差，避免上一个开关周期的误差累加到下一个开关周期，同时能够有效地抗输入侧电压扰动，具有很好的稳态和动态性能。内环电流算法即上一节推导的占空比公式。

电压外环主要是稳定输出电压波形，本文中的外环采用基本PI控制算法，基本PI控制算法的公式如下所示:

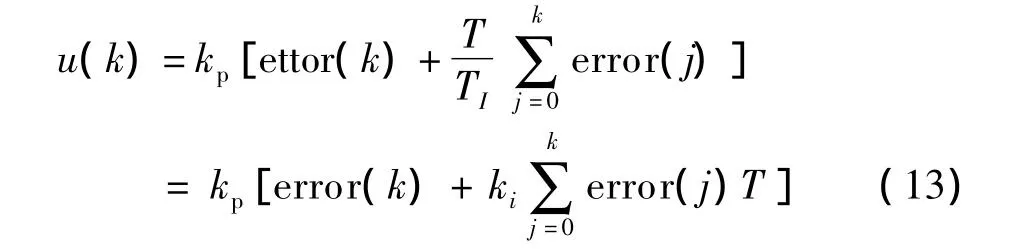
4 PSIM仿真分析

为了验证上述算法的可行性，分别对PI外环，P内环和PI外环，单周期内环的算法分别进行空载、半载(500W)和满载(1000W)的输出电压THD进行仿真分析。PSIM环境下的电路拓扑如图3所示。

图3 基于双Buck逆变拓扑的PSIM仿真图

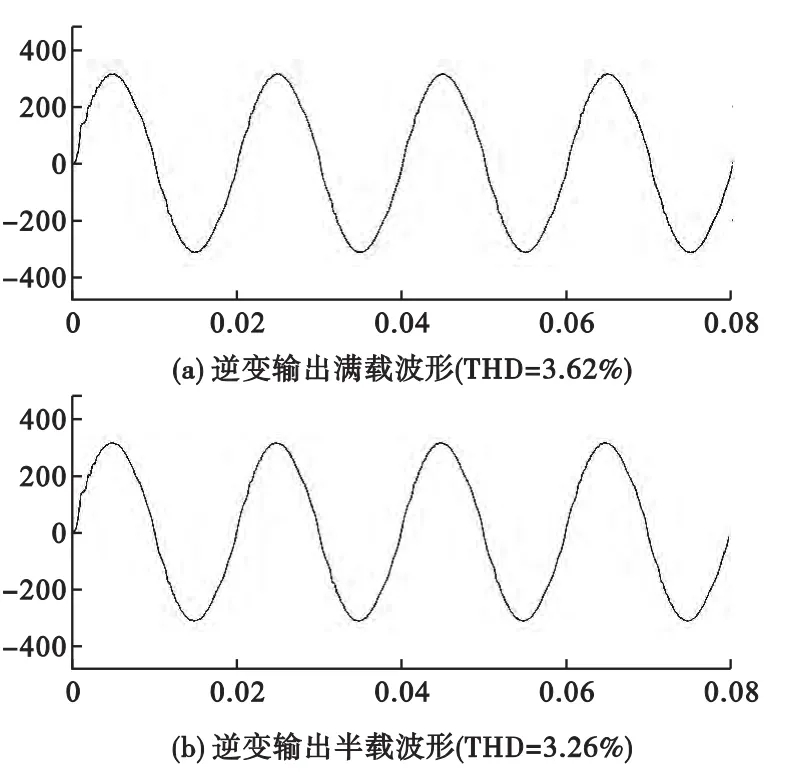
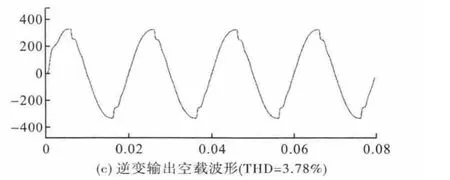
图4

图5

图4是外环PI控制，内环P控制产生的输出电压波形图，图5是外环PI控制，内环单周期控制的输出电压波形图，从上面的仿真波形分析看出，负载分别对满载、半载、空载的时候，当内环采用基于预测电流法的单周期控制的时候比内环采用比例调节控制的输出电压波形畸变率有了很大的改善。

5 结论

本文研究的双Buck逆变器，从拓扑结构上看，结构较为简单，由于开关管和续流二极管可以分别优化设计，具有损耗小、效率高的特点，同时由于不需要设置死区时间，输出波形畸变率较低。由于整个控制系统采用的是数字化控制，比模拟控制电路的元器件少了很多，简化了控制电路的设计。数字控制采用双环控制，内环采用了基于预测电流法的单周期控制算法，进一步降低了输出电压波形畸变率。

［1］张先进，龚春英.一种SPWM控制双Buck半桥逆变器研究［J］.电气传动，2009，39(2):48－51.

［2］洪峰，刘军.滞环电流控制型双BUCK逆变器［J］.电工技术学报，2004，19(8):73－77.

［3］陈坚.电力电子学—电力电子变换和控制技术［M］.北京:高等教育出版社，2004.

［4］Zargari N R.Two Switch High Performance Current Regulated DC/AC Converter Module［J］.IEEE Transactions on Industry Applications，1995，31:583－589.

［5］Gerald R Stanley，Kenneth M Bradshaw.Precision DC to AC Power Conversion by Optimization of the Output Current Waveform the Half Bridge Revisited［J］.IEEE Transactions on Power Electronics，1999，14(2):272－280.

［6］万珍梅，马运东.单周期控制正负输出Boost PFC的研究［J］.电力电子技术，2008，42(9):12－14.