怎样对数学教学素材进行重组创新？

王志南

（南通市通州区西亭小学，江苏南通226301）

在数学教学实践中，我们常常会有这样的感慨，同样的教学内容，不同的教材处理方法，教学效果往往相去甚远。寻找最能促进学生数学思考，促进学生数学知识、技能整体建构的教学素材重组创新策略，也就必然成为当下小学数学教学研究的重要内容。

事实上，研究教学素材的加工重组，不能仅仅局限于具体的数学问题情境的重组，更要研究学生数学知识建构过程中的素材重组，引领学生进行切入问题实质的“真研究”，获得有价值的“真发现”“真感悟”，进而引领学生对问题的思考由“表层”进入“深层”，直抵数学学习内容的内核和本质。那么，在数学教学实践中，我们又该怎样对数学教学素材进行重组创新，实现教学效能的最大化呢？本文结合自身的教学实践和探索，谈一谈自己的思考和见解。

一、寻根就源，挖掘教学素材的初始“模型”

在数学教学中，我们常常习惯于用已有的教学经验去展开教学，同时又被教学经验所束缚，很难在原有基础上对教学素材的重组实现新的突破。要想创新性地重组教学素材，教师预设教学活动时，必须要思考，教学素材的本源在哪里？怎样以一种最为朴素的形式呈现？

如教学《圆的认识》时，教师总是习惯于从生活中的圆引入，然后让学生借助圆形物体，用圆规画指定大小的圆，再引导学生探究圆的特征。这样的学习活动总体而言，不能激发学生的学习内驱力，对学生没有太大的吸引力。教师要实现教材重组，必须寻根就源，向深处思考，没有圆形物体（或工具）可以画出圆吗？在没有圆形物体（或工具）的时候，我们怎样画出一个比较接近圆的图形？怎样让这个图形更接近一个规范的圆？基于这样的思考，我们可以展开如下设计：

（1）你能尝试直接用水彩笔画一个圆吗？（如图1）可以怎样修改使它更像一个圆？（左右压扁一点，如图2)引导学生发现可以通过四个提示点来画圆。

（2）（出示图3）2条长度相等的线段，这样摆可以画圆吗？怎样摆可以画？（出示图4）让学生再次尝试。

（3）怎样画才能更接近圆形？提示点该怎样添加呢？（出示图5）再次画圆。

（4）回顾反思：刚才是怎样画出这个圆的？（确定中心点和一个固定长度）。引导想象，当提示点越来越多时，这个图形就是一个——圆。启发思考：这些提示点有什么特点？

显然，这样的设计不仅是创新的，更是本真的，因为它回到了画圆活动的原始状态，退到了问题的源点。弗赖登塔尔说，数学实质上是人们常识的系统化，因此学生可以在教师的指导下，通过自身的实践活动来获取知识，这个过程被他称为“再创造”。[1]在上述的探究活动中，学生经历了这样的再创造的过程，并在这一过程中逐步发现“圆是无数个与圆心等距的提示点组成的图形”。

二、意义建构，引领学生把握数学本质内涵

郑毓信教授认为，我们应当以数学思想方法的分析来带动具体数学知识内容的教学，即通过相关内容的“理性重建”使数学课真正“讲活”“讲懂”“讲深”，使学生能真正理解有关的数学内容，而不是囫囵吞枣，死记硬背。[2]因此，教师在对教学素材进行加工重组时，必须深入地研究教学素材，挖掘教学内容中所蕴含的数学方法及数学思想，寻找对数学知识进行意义构建的生长点。这样的教学活动，必须以引领学生把握学习内容的本质规律为终极目标，让学生在学习活动中进行深入思考，从数学的本质内涵的角度来展开建构，使学生不仅能掌握具体的数学知识内容，也能领悟内在的思想方法。

具体地说，如在教学《找规律——间隔规律》时，许多教师往往只注重“找”规律，即出示情境图让学生先认识情境图中的间隔现象（夹子与手帕、兔子与蘑菇、木桩与篱笆），并让学生在表格中填写相关数量的个数，研究间隔排列中有怎样的规律。然后再让学生用小棒和圆片也尝试摆出具有这样规律的间隔排列。这样的“找”显然是浅层次、浮于现象表面的，因为，从学生对规律的意义理解来讲，学生并没有弄明白为什么“首尾物体相同时，两端物体会比中间物体多1个”；从规律的发现方法而言，用不完全归纳法来探索发现一个规律有其必然的局限性；从规律的探究过程来看，教师并没有引导学生对情境图进行必要的抽象、重组，引导学生发现规律的普遍性。究其本质，教师未能从间隔规律中挖掘其蕴含的数学思想方法（一一对应思想），导致教学中的“看图说话”规律探究未能发挥其应有的教学价值。

图1

图2

图3

图4

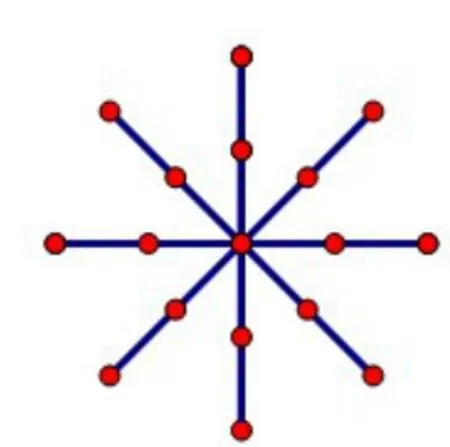
图5

图6

图7

图8

图9

图10

那么，怎样才能让“找规律”教学从简单的不完全归纳中抽离出来，走向深入和深刻呢？那就需要教师对教学素材进行重组，挖掘间隔规律中的对应思想，让学生进行意义建构，获得对规律本质的深入而透彻的理解。我们可以这样展开教学：

（1）猜一猜：（出示图6）继续排下去，下一个会是什么图形？为什么？揭示这样的排列在数学上称为一一间隔排列。

（2）启发思考：将图6中的正方形和三角形的个数进行比较，你发现什么?(个数相等)你是怎样看出这两种物体个数相等的？（数的方法、用一一对应的思想进行思考，相机出示图7）

（3）观察比较：（出示图8）让学生观察并比较两组图形排列的异同，引导学生发现图6中首尾物体不同，图8中首尾物体相同。而后引导学生发现图8中正方形和三角形一一对应后，还多一个正方形。

（4）抽象提升：（出示图9，图10）分别引导学生思考图9中正方形与三角形的数量之间的关系，进而发现规律：首尾物体不同，两种物体数量一样多；首尾物体相同，两端的物体数量比中间物体数量多一个。

（5）出示课本中的情境图，引导学生观察并思考，说一说自己的发现。

显然，当我们在进行教学素材的重组时，注重数学意义的构建，以数学思想方法的分析来重组具体教学素材，我们的数学教学才会更鲜活灵动，具有内在的思想性和深刻性。

三、重组活动，发掘探究活动的潜在价值

在数学教学素材的组织和运用中，教师一般均能根据教学目标设计一些数学探究活动，意在让学生在探究活动中自主地发现和生成数学知识。但在设计具体的探究活动时，教师往往容易被已有的经验所“遮蔽”，所设计的活动虽然能够激发学生的兴趣，引导学生进行观察、比较、分析等一系列思维活动，但教师的预设并未能有效引导学生对所进行的活动进行内化，发掘探究活动对数学知识构建的潜在价值。

如在教学《长方体和正方体的认识》时，教师在学生认识长方体的面、棱、顶点后，出示“研究提纲”，引导学生展开小组探究学习。

研究提纲：

（1）长方体有几个面？面的形状和大小是怎样的？

（2）长方体有多少条棱？棱的长短有什么关系？

（3）长方体有多少个顶点？

上述的探究活动固然可以让学生发现长方体的特征，但问题是，这样的探究仅仅局限于观察、比较等浅层次的思维活动，获得的活动体验难以深刻，所获的结论也仅仅是一种发现。显然，我们必须更加重视对于探究活动操作层面的必要超越，努力实现“活动的内化”。那么，怎样创新重组探究活动，发掘数学探究活动的潜在价值呢？

在上述案例中，在研究长方体棱的特征时，教师可以重组探究活动，变“简单观察”为“做中思考”，不再直接出示长方体让学生观察，而是提供给学生一些颜色不同的小棒和接头，让学生小组合作，自主搭一个长方体框架，然后让学生交流自己在搭的过程中的收获。在研究长方体面的特征时，教师可以变“讨论发现”为“想象配面”，通过出示长方体一组长、宽、高的数据示意图（如图11），想象它的六个面应该是什么样子？并提供相应的长方形让学生进行选择。

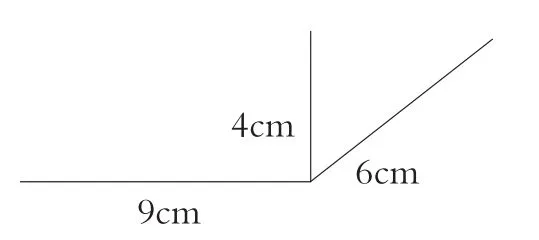
图11

这样的活动重组设计，充分发掘了探究活动对学生知识构建的潜在价值，可以有效引领学生深入到探究活动中去，并在活动中进行感知、分析、思考、想象和推理等一系列思维活动，实现数学活动的内化。进而促使学生真切地把握长方体的棱、面的内部结构，促进学生认知体系的建构和完善。

事实上，数学教学的创新归根结底就是对数学教学素材的重组创新，而对教学素材不断重组创新的过程，也是教师不断深入分析教材、解读教材、运用教材的过程。要实现教学素材的重组创新，不仅需要教师掌握教材重组的方法和策略，还需要教师不断丰厚自己的数学素养，开拓思想，抛开已有经验的束缚，创造性地对数学教学展开研究。▲

[1]弗赖登塔尔.数学教育再探——在中国的讲学[M].刘意竹，等，译.上海：上海教育出版社，1993.

[2]郑毓信.数学思维与小学数学[M].南京：江苏教育出版社，2008：170.