《认识分数——分一分（一）》教学设计

彭长江　洪志华

磨课心得

《认识分数——分一分（一）》这节课是在学习整数知识的基础上进行教学的，是数概念的一次扩展，是认识分数的第一阶段。三年级学生以前已学过整数，并且在日常生活中听到过分数。所以，教学要贴近学生已有的认知和生活经验，通过一根“线”把所有的“数”贯穿起来， 于是，我用数学大师华罗庚的话：“数起源于数”，联系华应龙这位名师把“分数”理解成先分后数（先数一共有几份，再数其中的份数，不过在数之前要看是否平均分）。抓住一个简简单单的“数”字，把“整数”和“分数”紧密联系起来，将“分数”分的动作、过程、结果用“数”字巧妙结合起来。让学生感悟数学是整体、联系、发展的，而不是孤独的分数。简简单单一条线，一站到底，体现了简约富有实效的课堂。让学生腾飞，飞得很高、很远。的确，以1个蛋糕为标准去度量，结果如果满几个蛋糕就用数字几表示；如果不满一个蛋糕，就用真分数来表示。这样，把新的学习内容纳入已有的认知框架，着眼点不仅是帮助他们把握分数的本质，渗透分数的模型思想。更在于培养学生以“系统”的眼光看待数学知识，进一步强化知识结构的完整性。

教学内容：北师大版三年级下册第67-69页。

教学目标：

（1）结合具体情境，初步理解分数的意义，体会学习分数的必要性。

（2）知道分数各部分名称，能正确读、写分数。

（3）结合折纸、涂色的活动，初步认识分数，体验数学与生活的联系，帮助学生发展，激发学习热情

教学重点、难点：学生在丰富的体验中，理解分数是一个相对概念，表示平均分后，结果中的一份或几份与总量间的关系。

教学过程

一、以旧引新，揭示课题

（1）说“整数”。关于数，华罗庚大师说过：“数起源于数。”接着，依次出现蛋糕的个数，指出有几个蛋糕就用数字几表示。

（2）说“分数”。师：指着大屏幕问：这是几个蛋糕？（半个）这一半，应该用什么数表示？12是怎么数的？

【设计意图：找到学习的起点，把整数和分数联系起来。分数怎么数？让学生带着问题，学生新课，打开学生思维的闸门，为后面的整体建构打下基础。】

二、循序渐进，全面理解12

活动一：学生折纸 课件演示

师：用圆片代表蛋糕，学生用自己喜欢的方式表示12，也就是一半。

生：交流汇报。

师：演示，把一个蛋糕从正中间分成2份，其中1份就是它的12。

【评析：通过课件演示，帮助学生建立12的表象，为下面全面的学习“分数”作了有效引领。】

活动二： 12正、反例，内化 12。

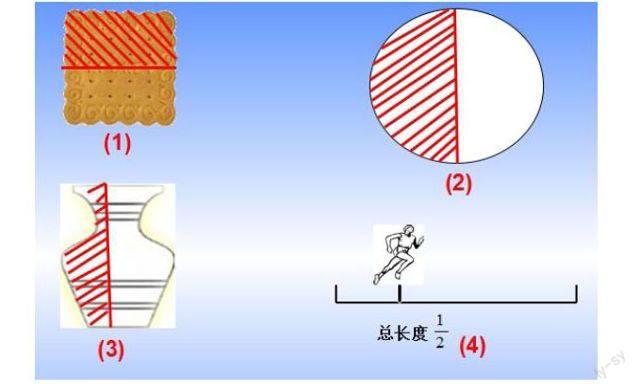
屏幕出示：

师：笑笑和我们一起学习了12，也用12表示图中的阴影部分，哪些是对的？哪些是错的？为什么？ 生：3、4是错的， 1、2是对的。师：第3图，为什么不能用12表示？师：看来，要用12表示，每份必须分得一样多。数学上把每份分得同样多，这种分法叫做怎么分？生：平均分。第3、4个要用12表示，应怎么办？

小结：看来，分数离不开平均分，它们是一对好朋友。

师：这4幅图（正确的图）形状、大小都不一样？为什么都用12表示？

小结：一个物体或图形，只要平均分成2份，其中的1份，就是它的12。

师：这些阴影部分，提问：它们分别是谁的12？

小结：在说分数时，一定要说清楚到底是谁的12。

师：说一说生活中的12。生：把一个西瓜平均分成2份，每份就是其中的12。师：12能表示这么多意思，数学真的是太神奇。指着饼干图问：图中的12是怎么数出来的？生：2份表示总共有2份，1份就是图中的阴影部分。

小结：数的方法：先数一共有2份，再数其中的1份。

【评析：12虽然是一个分数，表示分的“结果”，但每个分数都是“过程”和“结果”的统一。结果的意义就在于过程之中。初步感受分数和整数一样都要数，不同的数要先数总共有2份，再数其中的1份。其次，有利于培养学生对相关数学知识进行“分析与整合”。】

活动三：“会变的三角形”

任务一：猜一猜。 师：拿出一个图形的12，猜一猜：它整个图形是什么样子的？生：三角形。生：长方形。

师：老师变魔术，验证猜想结果是否正确。同学们，看这是什么图形？（把图形的12展开，得到一个正方形后恢复原状）生：长方形。（猜对的非常开心）

师：猜错的，还有机会。认真地看，不然就变不出来了。再把图形的12展开，看这是什么图形？生：三角形。（学生又高兴起来了）

任务二：由学习12迁移到13、23。

师：老师把图全部展开，现在阴影部分是整个图形的几分之几？ 生：13。

师：同样是这块阴影部分，怎么一会用12，一会用13，这是怎么回事？

生：长方形总共有2份，阴影部分是其中的1份，所以就是12；梯形总共有3份，所以就是13。

小结：所以我们在找分数的时候，要数清楚一共有几份。

师：追问：再涂一份，阴影部分是整个图形的几分之几？

任务三：认识分数各部分名称、意义。

（1）揭题。

（2）思考：图中的“3”、“2”、分数线分别各表示什么？（“3”表示总共有几份，“2”表示其中的几份。这3份是平均分出来的。）

（3）学生自学分数各部分的名称、读法。书空写法。

【评析：符合学生的认知规律，合理设计了适合学生学习的教学过程。学生在情境猜想中，积极地参与到学习中来，让学生思维内部真正动起来，真正体验到数学有理性的深邃，也有感性的快乐。】

任务四：整体构建

师：分数和整数都是数，分数要怎么数？先数什么？再数什么？

生：先数分母一共有几份，再数其中的份数。

师：分数啊，分数你到底是什么东西呀？其实很简单就是先分后数。你看，用一个简简单单的“数”字就把整数和分数联系起来。

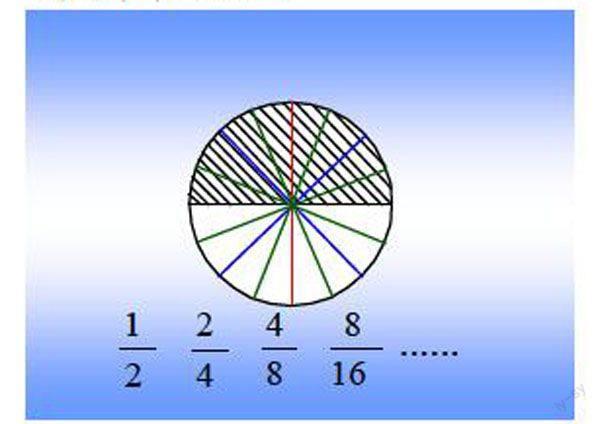
课件演示：

师：先出示一个空白的圆形。请看老师这样切（平均分成8份，阴影是4份），可用哪个分数表示阴影部分？如果阴影部分不用48表示，你还能用哪些分数表示？ 生：12、24、816。

师：请你说一说，你是怎么想的？请你上来，指一指你把多大的看作1份。

师：分一分：把一个圆形平均分得到不同分数的过程。

小结：原来数是有学问的，同一块阴影部分，用不同的标准数，就得到了不同的分数，学数学要善于从不同的角度去思考问题。

【评析：数学教学强调的不应该是孤立的数学知识的积累，更重要的是用联系与发展的数学眼光学会对相关内容进行“分析与整合”。学生感悟到的是数学是整体、联系、发展的，而不是孤独的分数。把新的学习内容纳入已有的认知框架，培养学生以“联系发展”的眼光看待数学知识，进一步强化知识结构的完整性。】

三、巩固与应用

创造自己喜欢的分数，可以折、可以涂，与同学交流，这个分数表示什么？

四、课堂总结

（1）这节课给你印象最深的是什么？

（2）解决问题。

【评析：回顾“印象最深”的片断，进一步树立学生学习数学的信心和乐趣；“解决问题”凸显学习数学的价值，提升数学素养。】