光伏发电系统中一种蓄电池状态估计的新方法

翁 珏

（广东省建筑设计研究院，广州 510000）

伏发电系统中蓄电池承担存储光伏电池板产生电能的供电任务，蓄电池荷电状态SOC（State-of- charge）是确定仅对本地负载供电或将电能上传电网的判断依据[1-2]，其开路电压为预上传的电能是否符合上传电网的标准提供依据[3]。蓄电池具有充电电流不稳定、充放电随机、易受环境温度影响等特点，是一个典型的强非线性系统。近几年国内外对电池状态估计提出了多种方法，如文献[4]提出了利用神经网络算法对蓄电池状态进行估计，文献[5]采用Sigma-point 卡尔曼滤波对蓄电池状态进行估计。但以上提到的估计方法普遍存在状态值估计精度不高，跟踪速度慢，跟踪曲线震荡剧烈，状态值估计误差大等缺点，针对以上问题，本文提出了一种新的蓄电池状态估计方法，基于渐消因子的Sigma-point 卡尔曼滤波估计方法（SFSPKF）。该方法基于Sigma-point 卡尔曼滤波（SPKF），在其滤波过程中加入渐消因子，对滤波过程中陈旧信息进行渐消，以提高滤波的实时性。仿真研究表明该方法在强非线性环境中，可取得良好的效果。

1 蓄电池电路模型

本文建立的蓄电池电路模型如图1所示，Vo为开路电压；Vp为分布电容上的电压值；Vq为储能电容上的电压值；Ro为欧姆内阻；Rp为电池内部极化电阻；Rq为充放电时的主体内阻；Cp为两个极板之间的分布电容；Cq为储能电容；I为主电路电流，Ip和Iq分布为两支路电流。

图1 蓄电池电路模型

根据基尔霍夫定律，可推导出

按照充放电特性，其开路输出电压为

由于信号采样周期时间极短，可认为在一个采样周期内，电流的大小基本不变，即故可推算出

联解式（1）、式（2）和式（3）可推得

根据蓄电池充放电特性可得到电池SOC 模型为[6]

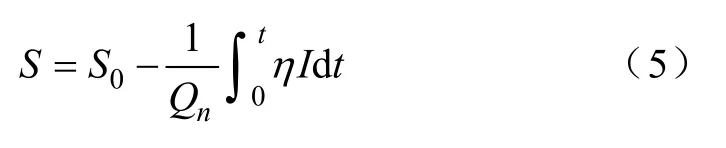
式中，S为电池荷电状态的估计值，S0为荷电状态初始值，Qn为额定容量，η为库伦系数，I为充放电时的电流。

由式（1）、式（4）和式（5）可得蓄电池的离散化后的卡尔曼滤波状态方程和系统的输出观测方程如式（7）和式（8）。

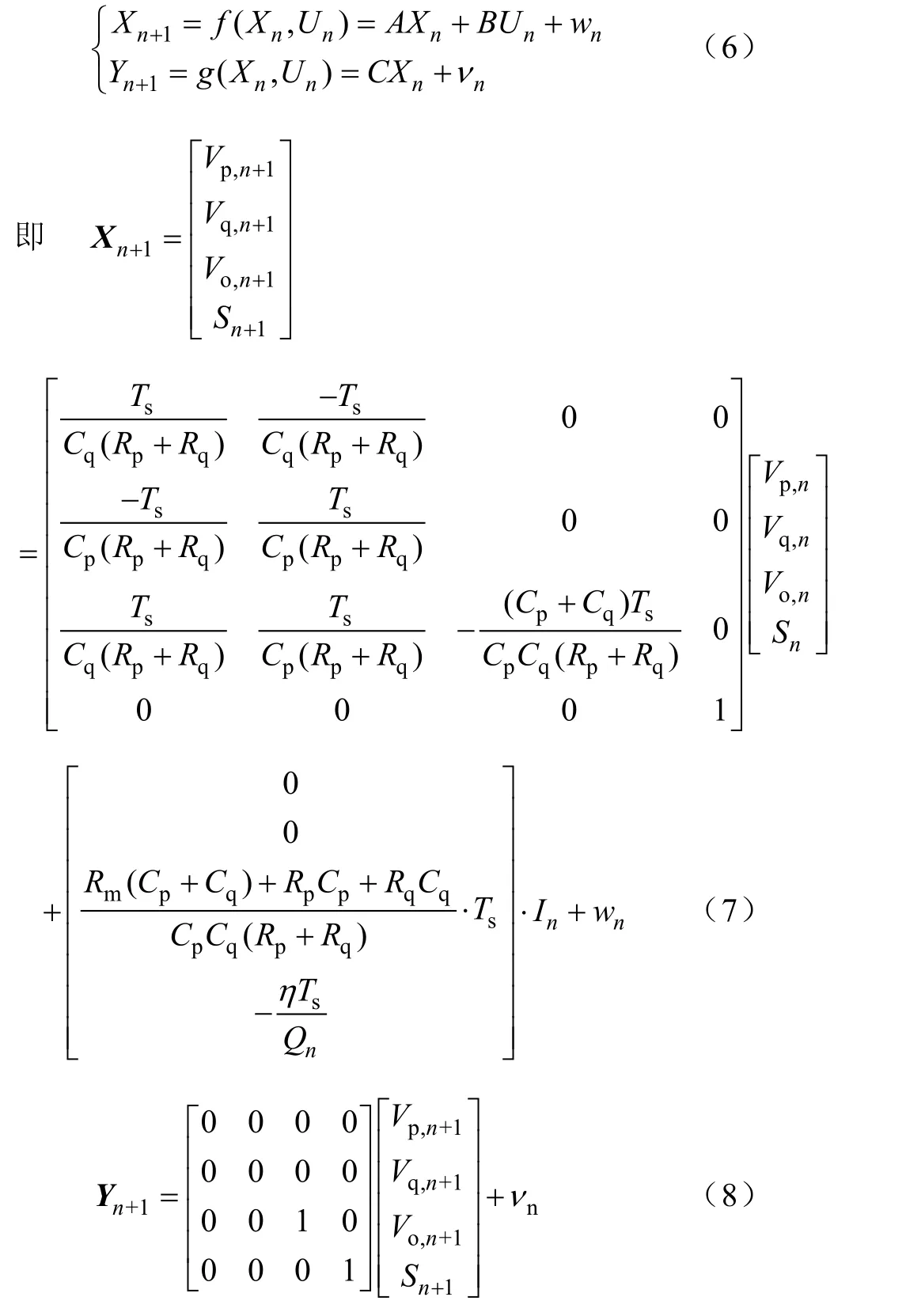
式中，Ts为信号采样周期，w(n) 和ν(n)分别为系统噪声和观测噪声，其为均匀分布的零均值高斯白噪声， 协方差矩阵分别为和

2 基于渐消因子Sigma-point 卡尔曼滤波

2.1 Sigma-point 卡尔曼滤波

Sigma-point 卡尔曼滤波，简称为SPKF，是一种基于Sigma-point 方法对非线性系统进行数理统计并估计系统状态和输出量的滤波方法[7]。

首先将状态变量Xn扩展为实际状态量xn、系统噪声wn和观测噪声νn，即

基于前次的状态量得到扩展状态的均值和方差，再选择2L+1 个采样点，L为状态量扩展后的维数，采用蓄电池电路模型L取6，然后通过状态方程得到扩展状态均值和扩展状态方差。

扩展状态均值：

扩展状态方差：

其次，确定采样点序列

确定采样点S= ｛ωi,χn|i;i= 0,1,… ,12｝，其中χn|i为选取采样点

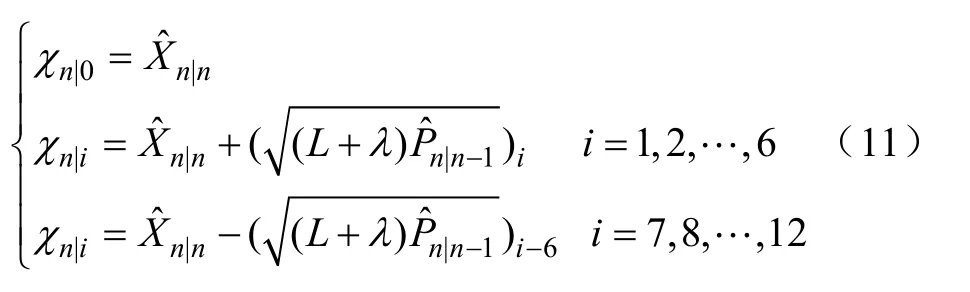
ωi为相对应的加权系数为

式中，λ=α2L-L，α为控制采样点分布距离参数，且 10-2≤α≤ 1；β减少高阶项误差的参数，取其高斯先验分布最优值β= 2；ωi(m)和ωi(c)分别为采样点均值和方差的加权系数；的平方根矩阵的第i列。

系统状态的一步预测为

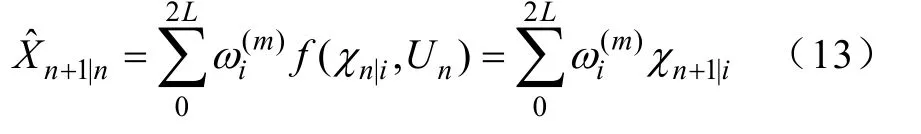
系统状态协方差估计为

系统观测输出估计为

系统输出残差序列为

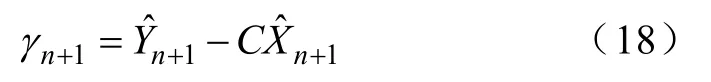
系统输出残差序列协方差为

最后计算卡尔曼滤波增益。

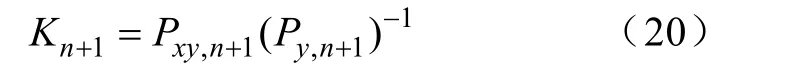
更新状态为

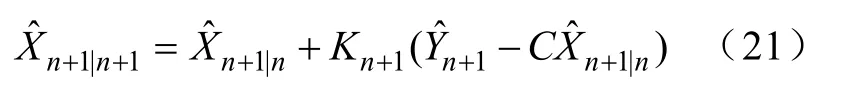
更新的状态协方差为

以上就是Sigma-point 卡尔曼滤波的迭代过程，只要确定了蓄电池系统状态均值和方差的初值，就可实现对蓄电池系统状态进行最小方差的估计。

2.2 渐消Sigma-point 卡尔曼滤波

由于蓄电池工作环境温度、湿度变化大，且其充放电具有随机性，充放电是一个复杂的非线性过程，参数检测必然存在误差。Sigma-point 卡尔曼滤波是一种基于记忆增长的滤波方法，其陈旧的估计数据对更新的状态估计值常常产生不良影响，甚至可能导致滤波发散，为了提高滤波器的跟踪能力和鲁棒性，本文提出一种渐消Sigma-point 卡尔曼滤波算法，简称SFSPKF，即在SPKF 滤波迭代过程中加入变化的渐消因子。

将滤波器中的系统状态协方差估计式（14）改为如式（23）。

其中λn+1≥ 1为渐消因子，渐消因子的作用在于实时地调整系统状态的协方差，以达到对非当前滤波产生的滤波值进行渐消目的，使之即使在过程参数变化的情况下，也能得到比较精确的状态估计值。

输出残差序列是衡量滤波性能的重要指标，从物理意义理解，当其弱自相关时，表示残差序列中的一切有效信息都被滤波器提取出来，故通过选取适当的渐消因子λn+1 ，可使系统输出残差序列弱自相关,从而抑制滤波发散。

当残差序列的期望值EVn+1≈ 0，可得如式（24）的渐消因子λ(n+ 1)表达式。

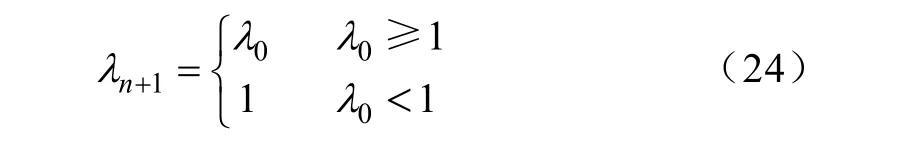
由上述，可构成渐消Sigma-point 卡尔曼滤波，如式（25）所示。

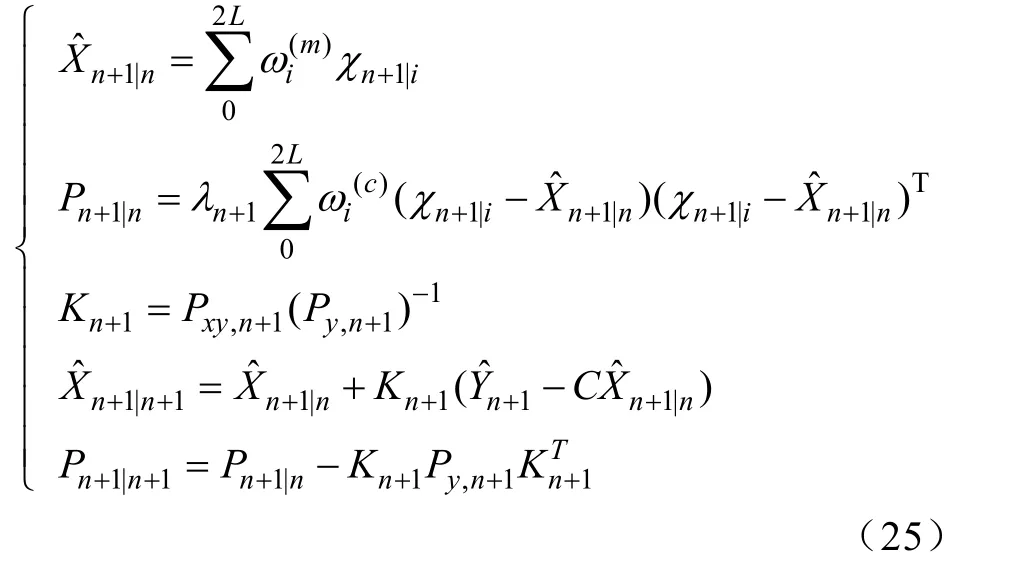
3 研究结果及其分析

根据检测不同环境温度和不同放电电流对电池放电的速率影响，运用最小二乘法可得到，在室温25℃，放电电流为6A 的情况下，可得η= 1.038；根据电池复合脉冲功率实验，电池静置实验和蓄电 池电路模型[8]，可得Ro= 0.2622Ω，Rp= 0.2582Ω，Rq= 0.0022Ω，Cp= 60.4102F，Cq= 56.18F。

蓄电池充放电工作过程的仿真研究结果如图2所示。根据对蓄电池工作电流的实际测量，可知工作电流是变化十分剧烈的，其电流均值在6A 左右。

3.1 渐消因子对状态估计的影响

在渐消Sigma-point 卡尔曼滤波中，渐消因子λn+1是一个根据协方差不断调整的因子，其表达式如式（24）所示，如将渐消因子设定为一定值1，即λn+1= 1，其与原滤波方法的对比图，如图3所示。 图4中，line1 为渐消因子取定值1 的蓄电池状态估计曲线，line2 根据原滤波方法，即渐消因子根据式（24）取值的状态估计曲线。

图2 蓄电池工作电流

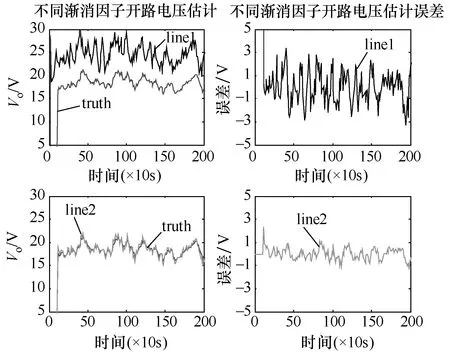
图4 不同渐消因子对开路电压估计

图3、图4为不同渐消因子估计精度对比图，表1、表2为其精度指标对比表，由表可见line2 估计精度更高。

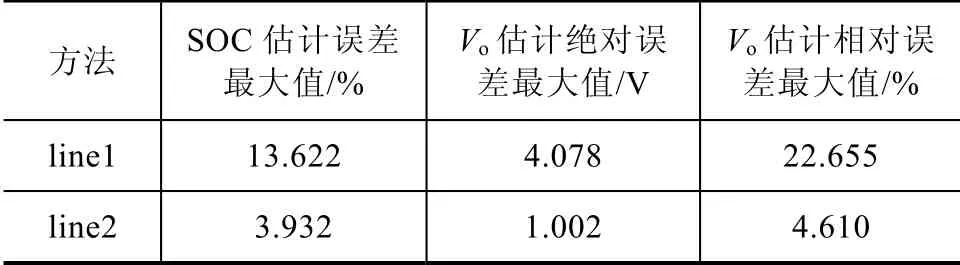
表1 不同渐消因子误差最大值比较

表2 不同渐消因子误差绝对值的平均值比较

3.2 不同滤波方法对状态估计

由于充放电过程具有随机性，为了正确估计蓄电池的SOC 和开路电压V0，这里讨论了3 种不同的卡尔曼滤波方法，以便比较滤波效果的优劣。

图5、图6为不同滤波方法估计精度对比图，表3、表4为其精度指标的对比表，由图和表可以见，SFSPKF 的估计精度最高。

图5 不同滤波对蓄电池SOC 估计

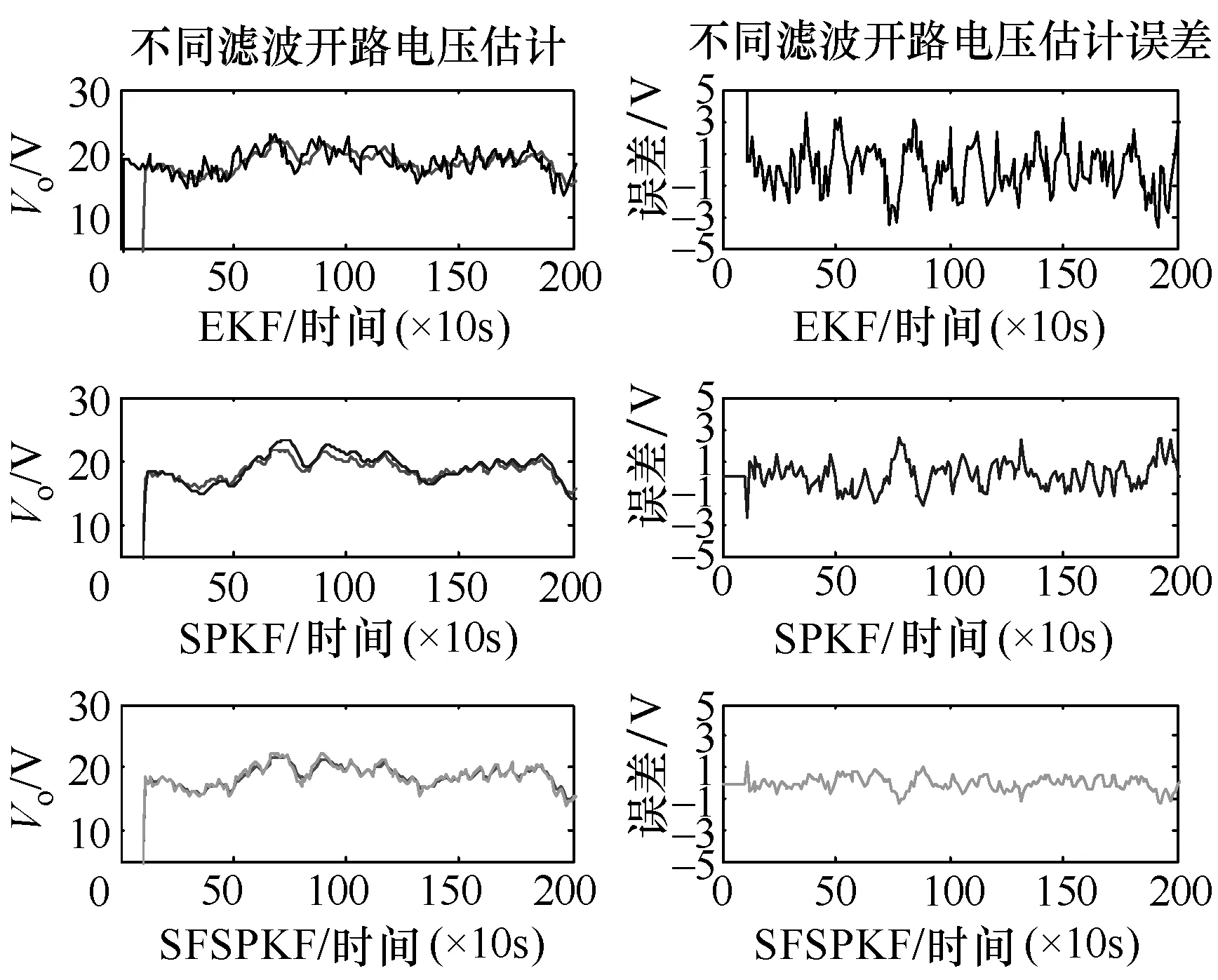
图6 不同方式对蓄电池开路电压估计

图7 渐消因子取值曲线

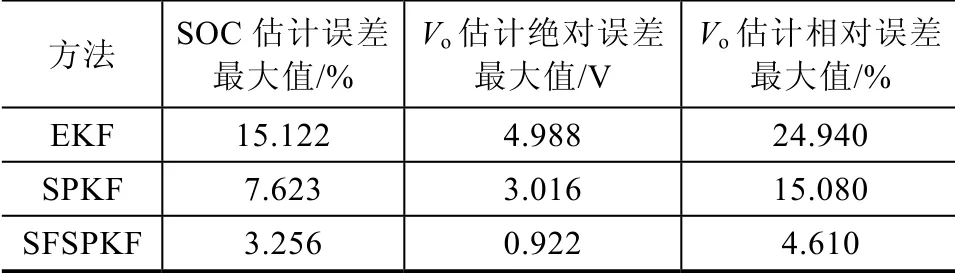
表3 不同估计方法误差最大值比较

表4 不同估计方法误差绝对值的平均值比较

4 结论

本文建立了光伏发电系统的蓄电池电路性能模型，提出了一种基于渐消Sigma-point 卡尔曼滤波方法。仿真研究对比研究结果表明，SFSPKF 较EKF和SPKF 跟踪精度更高，跟踪速度更快，最大估计误差值最小，且估计曲线波形更加平稳，是对蓄电池观测和管理的一种可行方法。

[1] 梁爽,李宁宁,纪延超,等.带蓄电池储能的静止同步补偿器的小信号模型建立及其控制[J].电气技术,2014,8(6): 1-4,30.

[2] 李锐,李鹏.储能系统在孤岛微网中应用[J].电气技术,2014,8(6): 15-18.

[3] Jin Longzhang.Battery state-of-charge estimation based on sigma point kalman filter[C]//2nd International Conference on Digital Object Identifier,2011: 3816- 3819.

[4] Wei Jian,Jiang Xuehuan,Zhang Jinliang.et al.Comparison of SOC Estimation Performance with Different Training Functions Using Neural Network [C].computer society,2012 IEEE 14th International Conference on Modelling and Simulation,2012: 459-463.

[5] 戴海峰,魏学哲,孙泽昌.基于扩展卡尔曼滤波算法的燃料电池车用锂离子动力电池荷电状态估计[J].机械工程学报,2007,43(2): 92-95,103.

[6] 高明煜,何志伟,徐杰.基于采样点卡尔曼滤波的动力电池SOC 估计[J].电工技术学报,2011,26(11): 161-167.

[7] Liu Yunfeng,Zheng Kun,Xing Zhilong.Estimation of internal states of 18650 lithium-ion batteries by Sigma-Point Kalman Filter[C]//Electrical and Control Engineering (ICECE),2011 International Conference on,2011: 1067-1070.

[8] 徐杰.基于卡尔曼滤波的动力电池组SOC 精确估计[D].杭州:杭州电子科技大学,2009.