资源约束下项目调度鲁棒优化模型研究

陈伟伟，张云宁，欧阳红祥

(河海大学 商学院，江苏 南京211100)

资源受限的项目调度问题(resource - constrained project scheduling problem，RCPSP)是研究如何在同时满足项目任务之间的资源约束和时间约束的情况下，将有限的资源合理地分配给各个任务并确定任务的开始时间，使项目工期最短。该类问题虽然理论模型十分丰富，但求解相当困难，属于强NP -hard 问题，受到国内外众多学者的关注［1-3］。在考虑相互独立的多个项目与项目之间对共享资源竞争的情况下，进一步研究RCPSP，资源约束下的多项目调度问题(resource constrained multi-project scheduling problem，RCMPSP)就应运而生。

在建设工程多项目管理中，资源包括资金、劳动力、技术及管理人员、原材料、设备、外部协作单位等，难免会遇到资源冲突的问题。然而，多项目调度相比单个项目调度资源种类繁多，关系复杂。多项目调度问题无法像单个项目调度那样耗费全部资源去保证一个项目的顺利实施，而是必须先分析项目之间错综复杂的关系及资源的特点，权衡之后再将资源进行分配。鉴于此，将基于均值-鲁棒性模型、调度鲁棒优化问题，结合遗传算法对资源受限多项目进度计划进行研究。

1 多项目调度鲁棒优化模型

在实际执行过程中，调度的目标是提高调度方案的稳定性，通常吸收一部分可以预期的不确定事件的干扰来增强方案的鲁棒性。对任务工期不确定的资源约束下多项目调度问题建立鲁棒模型。项目管理人员可通过调整模型中参数的权重系数，得出若干个可行解和最优解，从而做出决策。

1.1 均值-鲁棒模型

在研究RCMPSP 时，每种模型都有优点和缺点，通常只关注于决策者的一方面，而忽略了其他方面。为了达到更多方面的折中，羊晓飞［4］提出了一种新的鲁棒优化模型，即均值-鲁棒优化模型。该优化模型中包含两层优化：

(l)第一层优化。不考虑鲁棒性的期望性能，以期望性能作为优化指标，其目标函数如下：

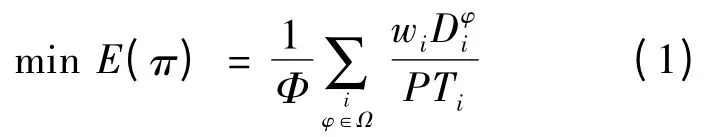
定义：坏场景φ∈Ωβ和坏场景集合Ωβ，令T=β×E*，β≥1，则可定义Ωβ⊆Ω 是一个场景的子集，表示给定的调度方案π 在实现时的性能大于给定值T的所有场景的集合，即：

(2)第二层优化。根据坏场景集定义鲁棒性度量RM(π)：

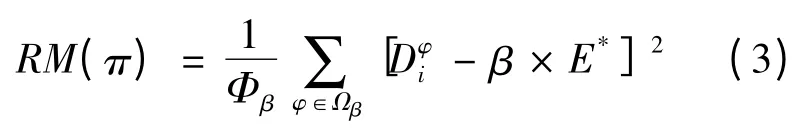
运用上述均值-鲁棒优化模型，考虑从单个最坏场景推广到多个坏场景组成的集合，提出了针对所定义的坏场景集的鲁棒优化准则。在该准则下，可在群体上抑制坏场景性能的恶化，达到项目管理人员在建设项目过程中抗风险的目的。

1.2 调度模型的假设

(1)RCMPSP 关系到一个共享资源库和若干个并行项目，且所有资源的供给量是有限的。

(2)对共享的有限资源竞争是若干个并行项目之间的唯一联系。

(3)并行项目之间互相独立，且项目之间不存在紧前关系。

(4)任务之间存在紧前关系，但不存在循环与反馈，且所有任务均需可更新的资源。

1.3 目标函数构建

在采用鲁棒优化模型研究RCMPSP 问题的过程中，国内外学者提出了不同的算法和规则。例如，在求解随机资源受限项目调度问题中，BALLESTIN 等［5］将情景集的概念应用于最优调度规则中;在离散情景的应用中，PADMAN 等［6］用其表示既定目标任务结束时间的不确定性，HERROELEN 等［7］用其表示任务工期的波动性。

然而，在大多数的研究中，多项目调度以所有项目延期加权最小为目标函数的模型中，并未考虑到项目延期与项目工期的关系，即项目工期越长，其延期时间越长的可能性越大。因此，基于单项目鲁棒调度原理，从所有项目延期加权与项目工期之比的角度出发，建立鲁棒的目标函数进行多项目调度问题研究。

由于各个项目任务工期具有不确定性，因此情景集Ω={1，2，…，Φ}为任务工期的随机性，情景φ∈Ω。在情景φ 下，第i个项目中第j个任务Aij的工期向量为在调度方案π 中，任务Aij的结束时间为则第i个项目的工期为所有任务的最晚完成时间取决于项目的调度方案π 和工期向量，即项目延期的情况取决于调度方案。据此所设计的鲁棒优化目标函数如下：

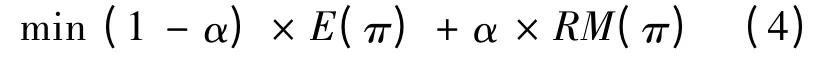
该目标是要找到满足资源及活动逻辑关系的情景φ，使得各项目延期与项目工期之比的加权与鲁棒性度量加权最小。其中，风险系数α∈［0，1］表示项目管理者抗风险偏向的程度。

1.4 调度模型的构建

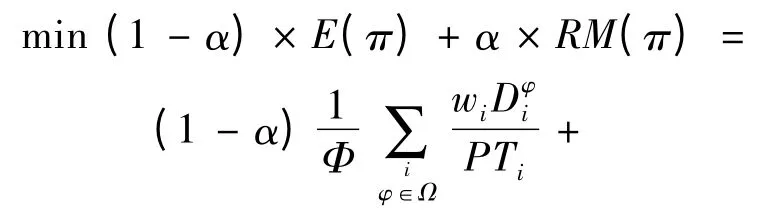
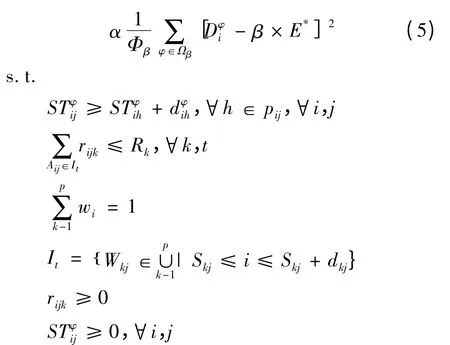
其中，It为第t阶段内正在进行的活动集合。

与传统的模型相比，该模型是一个覆盖面更广的鲁棒优化模型，通过两次求解资源受限项目调度问题，不仅大大降低了计算复杂性，而且具有理论和实际意义。另外，该模型应用于实际问题时，T=β·E*，β≥1 具有实际意义。如果把T看作项目管理者期望的项目工期延期与项目计划工期的加权，则式(2)表示所有超过项目管理者预期的坏场景集合，而式(3)则表示对所有超出项目管理者预期的坏场景的惩罚。在分析确定的任务时，在全部Φ 个情景中，可以近似拟合任务j的工期为任意概率分布。实际运用时，情景集由历史数据得到，任务的概率分布不需要了解，这使得的鲁棒优化模型更具有普适性和优越性。

2 鲁棒调度数学模型遗传算法求解

遗传算法(genetic algorithm，GA)是一种有效解决最优化问题的方法，可以较快地搜索到全局最优解，特别适用于多极点的优化问题。遗传算法对需要求解的目标函数形态没有明确要求，比传统的优化方法更加优越。在任务工期不确定的情况下求解鲁棒优化模型，一般先从全部情景中获得一个小样本，即Φ 个情景，用来对全部情景进行样本估计。因此采用小样本估计方法通过遗传算法来求解RCMPSP 鲁棒优化模型。

2.1 模型求解GA 算法参数和操作设计

根据GA 算法优化流程，对建立的鲁棒优化模型求解流程设计如下：

(1)编码方案。大多数学者运用遗传算法求解确定型RCPSP，采用任务列表法对染色体进行编码。为了能够给项目管理者提供良好的决策依据，求解的基准调度需要良好的稳定性和鲁棒性，通常采用直接表达方式。在用遗传算法求解鲁棒优化模型时，选取项目中每个任务的开始时间作为染色体π =(π1，π2，…，πj)，也就是把调度方案假定为遗传算法中的染色体［8］。

(2)初始种群。采用随机方法产生初始种群，使得各项目中的每个任务可以获得一个最早开始时间到最迟开始时间之间的随机值。

(3)适应值函数。针对鲁棒优化模型，设计适应值函数如下：

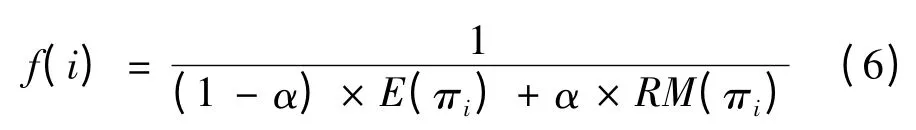
其中，f(i)为当前代中染色体i的适配值，在Φ种情景下如果目标函数值越小，则算法中个体的适应值越大。πi为第i个染色体代表的调度方案。

(4)选择算子。采用赌轮盘选择法，将上一代的优先个体传递到下一代。每个染色体被选择的概率按照式(7)计算：

(5)交叉算子。采用单点交叉算子，选取一个随机交叉点，通过在交叉点上交换亲代的基因得到若干个子代染色体。其中交叉概率为pc。

(6)变异算子。通过交叉算子获得子代染色体后，再进一步使用变异算子优化调度方案。变异算子通过改变一个或若干个基因的值从而增加种群的多样性，设变异概率为pm。变异通常有3种方式：均匀变异、增量变异和非均匀变异。这里采用均匀变异算子。

2.2 模型求解GA 算法步骤

资源约束下的多项目调度问题的鲁棒模型具体求解步骤如下［9］：

(1)初始设定遗传算法中的每个参数，并读取全部的情景样本值;

(2)根据给定各项目中的每个任务分配一个最早开始时间和最迟开始时间之间的随机值生成初始种群，根据式(6)计算每个个体的适应值;

(3)根据式(7)选择个体，采用概率pc、pm分别进行交叉运算、变异运算;

(4)重复步骤(3)直到新一代种群产生;

(5)按照式(6)计算当前种群中每一个个体的适应值，并保留和记录最佳个体;

(6)当迭代次数达到规定的代数，转步骤(7);否则，迭代次数加1，返到步骤(3);

(7)输出最佳个体，终止程序。其中最佳个体为项目调度问题的最优鲁棒解。

3 仿真算例

采用Matlab 软件对给出的一个算例进行仿真调度，选取文献［10］中的算例进行求解分析。该算例含有3 个不同网络结构的项目，其网络活动如图1 所示。这3 个项目分别由6、8、7 个活动组成，所有活动共享4 种资源(r1，r2，r3，r4)，每个资源的约束总量为4。每个项目的计划工期和需求的资源量如表1 和表2 所示。3 个项目的重要性权重分别为w1=0.5、w2=0.3、w3=0.2。3 个项目具有相同的任务开工时间，在资源无约束的情况下项目的完工工期分别为13 d、13 d 和10 d，计划完工工期是23 d、23 d 和20 d。

图1 各项目的网络活动图

表1 各项目活动的持续时间

3.1 模型求解

假设项目中任务j的随机工期+3］中的一个正整数，从所有情景集中随机选取500 个情景作为项目实际的情景集合，再从实际的情景集合中随机选取50 个情景作为小样本进行求解，即Φ =50。假定总代数GEN=200，种群大小POP=20，交叉概率pc=0.6，变异概率pm=0.1，鲁棒优化模型中α=0.5，使用均匀变异算子求解。

通过逐步迭代进化搜索所有情景下的鲁棒调度方案，如图2 所示，遗传算法求解效果显著。随着代数的增加，目标函数值逐渐减小，在GEN=30 左右开始趋于稳定，第60 代种群的目标函数值与最初种群的目标函数值相比明显变小。

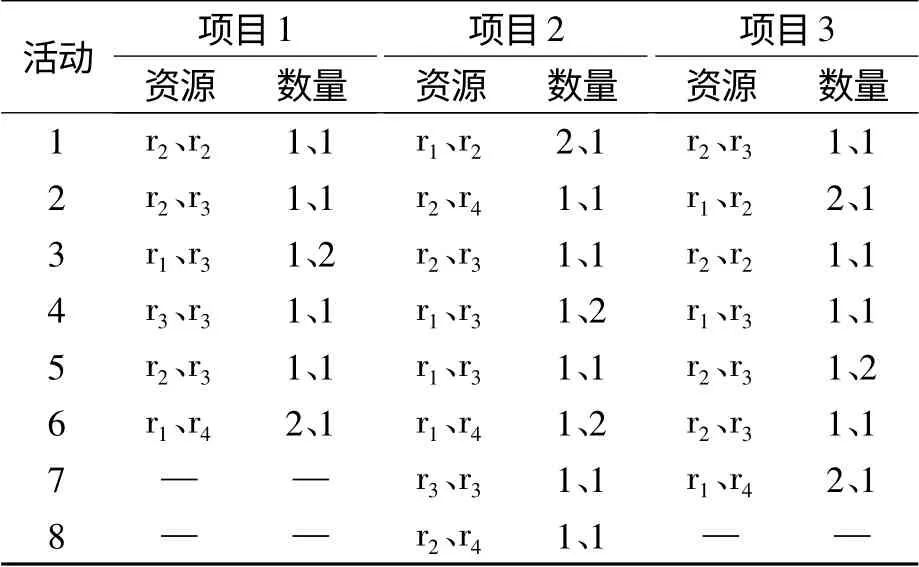
表2 各项目活动的资源需求

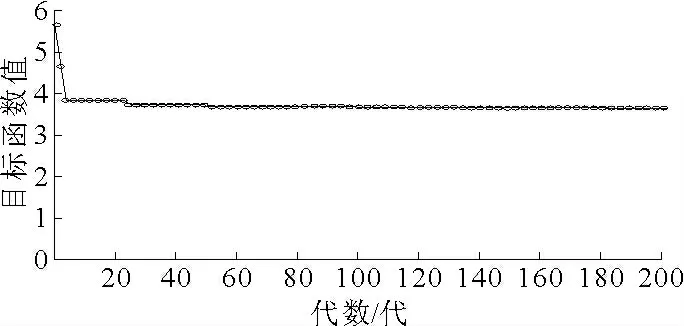
图2 遗传算法求解的进化过程

3.2 结果分析

为了表明上述的调度鲁棒优化准则的适用性，逐步调整风险系数α，每一个风险系数α 可以对应一个不同的调度方案。全部情景下调度方案的E(π)与RM(π)的变化如表3 所示。

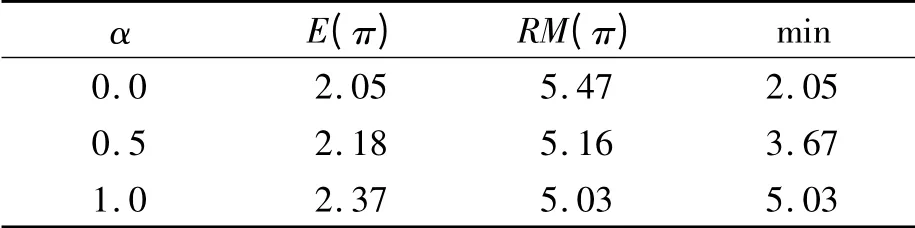
表3 风险系数α 对解的影响

由表3 可知，随着α 的增加，E(π)不断增大，RM(π)则逐渐减小。当抗风险系数α 选择较大时，项目工期的延期期望值会有所增大，但鲁棒性度量减小，即风险较大;当抗风险系数α 较小时，多项目调度方案有较小的进度延期期望值，但此时的鲁棒性度量较大，即风险较小;α=0 时，此时的鲁棒性度量最大，表明模型对项目风险控制具有一定的有效性。因此，项目管理者根据自身的风险偏好，选择符合项目实际情况的风险系数α，从而得到可以选择的多项目调度方案以供决策。

4 结论

建立了资源约束环境下的多项目鲁棒性调度模型，提出了多项目调度问题实现最大化的鲁棒性研究的一种算法。考虑到项目工期越长，其延期时间越长的可能性越大，采用了各项目工期延迟与活动计划工期之比作为指标，改进并建立了多项目调度模型。同时，在鲁棒模型的建立中，改进了传统鲁棒模型的不足，采用均值-鲁棒模型进行研究，能够更全面地提高鲁棒调度的抗风险能力，为项目管理者提供了新的决策方法。

［1］KOLISCH R，PADMAN R. An integrated survey of deterministic project scheduling［J］. Omega，2001，29(3)：249 -272.

［2］KOLISCH R，HARTMANN S. Experimental investigation of heuristics for resource - constrained project scheduling：an update［J］. European Journal of Operational Research，2006，174(1)：23 -37.

［3］寿涌毅.资源约束下多项目调度的迭代算法［J］.浙江大学学报：工学版，2004，38(8)：1095 -1099.

［4］羊晓飞.基于场景和模糊描述的不确定Job Shop 鲁棒调度［D］.济南：山东大学图书馆，2009.

［5］BALLESTIN F，TRAUTMANN N. An iterated -local- search heuristic for the resource - constrained weighted earliness-tardiness project scheduling problem［J］. International Journal of Production Research，2008，46(22)：6231 -6249.

［6］PADMAN R，ZHU D. Knowledge integration using problem spaces：a study in resource - constrained project scheduling［J］. Journal of Scheduling，2006，9(2)：133 -152.

［7］HERROELEN W，LEUS R. Project scheduling under uncertainty：survey and research potentials［J］. European Journal of Operational Research，2005，165(2)：289 -306.

［8］王伟.任务工期不确定的资源受限项目调度优化［D］.杭州：浙江大学图书馆，2010.

［9］寿涌毅，王伟. 基于鲁棒优化模型的项目调度策略遗传算法［J］.管理工程学报，2009(4)：148 -152.

［10］郑彦琦.基于活动成本目标的资源受限多项目进度计划［D］.武汉：华中科技大学图书馆，2007.