基于衡平矩阵的二元关系传递性的判别法

2015-05-25孙凤芝

大庆师范学院学报 2015年3期

孙凤芝

(大庆师范学院教师教育学院，黑龙江大庆163712)

0 引言

二元关系是离散数学集合论中重要的基本概念，实际判定某个二元关系性质时，自反性、反自反性、对称性的判定比较容易，而传递性的判定有时则较困难，是学习的重点，也是难点。特别是当集合中的元素个数较多时，其判断更为困难。本文实现了判断一个二元关系是否具有传递性变为判断它的关系矩阵是否为衡平矩阵的转化，从而可以准确而又迅速地实现二元关系传递性的判定。

准备知识

定义1 设A，B 为集合，用A 中元素为第一元素，B 中元素为第二元素构成有序对.所有这样的有序对组成的集合叫做A 和B 的笛卡儿积，记作A×B［1－3］.

笛卡儿积的符号化表示为

A×B={＜x，y ＞| x ∈A ∧y ∈B}［1－3］

定义2 设A，B 为集合，A×B 的任何子集所定义的二元关系叫做从A 到B 的二元关系，特别当A=B 时则叫做A 上的二元关系［1－3］。

定义3 对于A 是有穷集合时，设A={a1，a2，…，an}，R 是A 上的关系，

定义4 设R 为A 上的关系，若

∀x∀y∀z(x，y，z ∈A ∧＜x，y ＞∈R ∧＜y，z ＞∈R →＜x，z ＞∈R)，

则称R 是A 上的传递关系［1－3］.

定义5 设A=(aij)n×n，如果满足∀i，j，k=1，2，…，n，都有aikakj=aij，则称A 为衡平矩阵［4］。

定义6 设F，G 为二元关系，G 对F 的右复合记作F· G，其中

F· G={＜x，y ＞| ∃t(＜x，t ＞∈F ∧＜t，y ＞∈G)}

特别把R· R=R2［1－3］。

1 主要结论

引理1 设A={a1，a2，…，an}，R 是A 上的关系，则R 具有传递性的充要条件当且仅当R· R(R［5］。

证明必要性任取＜x，y ＞∈R· R

⇒∃t(＜x，t ＞∈R ∧＜t，y ＞∈R)}

⇒＜x，y ＞∈R (因为R 在A 上是传递的)

所以R· R ⊆(R。

充分性

任取＜x，y ＞，＜y，z ＞∈R，则

＜x，y ＞∈R ∧＜y，z ＞∈R，

⇒＜x，z ＞∈R· R

⇒＜x，z ＞∈R (因为R· R ⊆R)

所以R 是传递的。

定理1 设集合A={a1，a2，…，an}，R 是A 上的二元关系，R 的关系矩阵为AR=(aij)n×n令B=AR·AR=(bij)n×n，则R 是A 上传递关系的充分必要条件是:当bij=1 时，一定有aij=1 (注:此处乘法及加法分别为布尔乘法和加法)［6］。

证明必要性:设集合A 上的二元关系R 的关系矩阵为

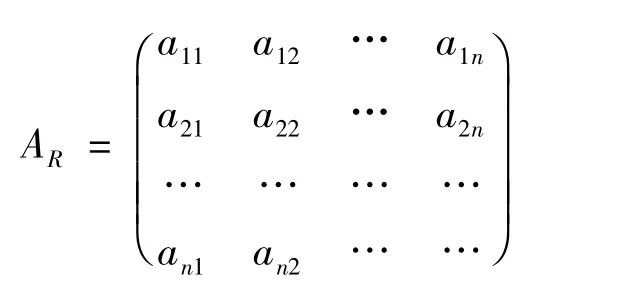
由矩阵的乘法运算规则可知

当然，其中的相加是逻辑加，即:1+1=1，1+0=0+1=1，0+0=0。

当bij=1 时，由求bij的算式(*)式可知，

至少存在一个k(k=1，2，…，n)，使aik(akj=1，

此时一定是aik=1 且akj=1，则有＜ai，ak＞∈R 且＜ak，aj＞∈R，

又由R 是可传递的，由传递性定义得:＜ai，aj＞∈R，即aij=1。

充分性:当bij=1 时，由求bij的算式(* )式可知，

至少存在一个k(k=1，2，…，n)，使aik(akj=1，

此时一定是aik=1 且akj=1，则有＜ai，ak＞∈R 且＜ak，aj＞∈R，

又由aij=1，即＜ai，aj＞∈R，

即当bij=1 时，有aik=1，akj=1，aij=1 同时成立，

从而有＜ai，ak＞∈R，＜ak，aj＞∈R，＜ai，aj＞∈R 同时成立，

由传递性定义可知:R 是可传递的。

定理2 设A={a1，a2，…，an}，R 是A 上的关系，MR是R 的关系矩阵，则MR为衡平矩阵充分必要条件是当且仅当R 具有传递性。

证明必要性由于R 是A 上具有传递性的二元关系，则ai，aj，ak∈A(i，j，k=1，2，…，n);若＜ai，aj＞∈R，＜ak，aj＞∈R，则有＜ai，aj＞∈R，也即aik=1，akj=1，aij=1;因而aikakj=aij;若aik与akj中至少有一个为0 时有aij=0，也有aikakj=mij。故∀i，j，k{1，2，…，n}，aikakj=aij，即MR为衡平矩阵。

充分性设MR为衡平矩阵，即aik，akj(i，j，k=1，2，…，n)有aikakj=aij;若aik=1，akj=1，则aij=1，所以有＜ai，ak＞∈R，＜ak，aj＞∈R，＜ai，aj＞∈R，即∀ai，aj，ak∈A(i，j，k=1，2，…，n)，＜ai，ak＞∈R，＜ak，aj＞∈R 则有＜ai，aj＞∈R，故R 是A 上具有传递性的二元关系。

由上述定理1 和定理2，很容易得到下面判定关系矩阵为衡平矩阵的定理及方法。

定理3 对于关系矩阵MR中的每一个非零元aij=1，将第j 行元素对应加(布尔加)到第i 行元素上去，如果运算后，矩阵有变化，则R 不是衡平矩阵;如果矩阵没变化，则R 是衡平矩阵。

证明设集合A={a1，a2，…，an}，R 是A 上的二元关系，其关系矩阵为

MR设MR中第i 行第j 列元素aij=1，现考察MR中第i 行元素与第j 行元素:

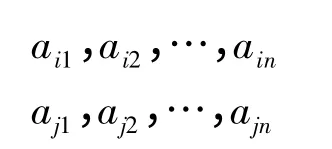
先将这两行元素作布尔加(0+0=0，0+1=1，1+0=0，1+1=1):ai1+aj1，ai2+aj2，…，ain+ajn，再与第i 行元素作比较，如果它们是不相同的，例如有aik和aik+ajk不同，这只有一种可能，即aik=0，aik+ajk=1 这也表明了当aij=1，ajk=1 时，而aik=0，这说明关系R 中存在着＜ai，aj＞∈R 和＜aj，ak＞∈R，而＜ai，ak＞∉R，所以R 不是传递关系，即R 不是衡平矩阵;

如果这两行对应元素是相同的，即对于任意的k(k=1，2，…，n)，aik=aik+ajk，这表明当ajk=1 时，必有aik=1，即当aij=1，ajk=1 时，必有aik=1，这说明关系R 中对于任意的k(k=1，2，…，n)，当＜ai，aj＞∈R 和＜aj，ak＞∈R 时，必有＜ai，ak＞∈R，则R 是传递关系，即R 是衡平矩阵。